哈夫曼编码唯一吗_平均编码长度怎么求

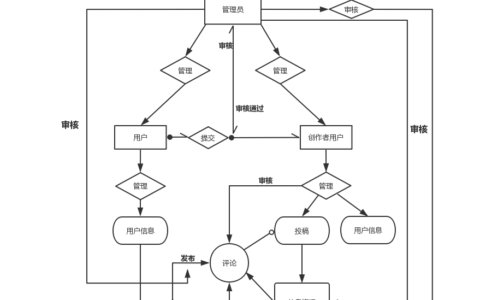
实现通用人工智能的可能道路：无损压缩！　　在 2022 年末突然出现的 ChatGPT 令人赞叹不已。 GPT-4 的推出更是让人觉得它已经达到了早期通用人工智能（AGI）的水平。实际上，OpenAI 多年来一直秉持着一系列明确的行为准则来指导其技术发展思路。在本文中，我们将深入分析并进一步拓展 OpenAI 长期以来所坚守的一项重要准则：无损压缩是达成 AGI 的一条有效路径。　　整篇文章主要分为以下几部分：编码与无损压缩：主要介绍常用的编码，无损压缩的基本概念。自回归与无损压缩：主要介绍如何利用自回归模型进行无损压缩，并做了严格的数学证明。无损压缩的极限：主要介绍柯氏复杂度和 AGI 的关系。　　写这篇文章的原因有两点：目前互联网上关于压缩即智能的解读文章都是错误的，错误的地方在于错误的使用了算术编码技术。这篇文章的其中一个目的是纠正这个严重的错误。无损压缩的背后有着更深刻的哲学意义。本文将尝试从信息论中的信息熵延伸到算法信息论中柯氏复杂度。探索无损压缩的极限是什么，通用人工智能的边界又在哪里。（巧合的是，我刚写完这篇文章的草稿，我就在油管上看到了 OpenAI 首席科学家的演讲，他也提到了柯氏复杂度和无损压缩的关系，说明英雄所见略同，啊哈哈！）　　一、编码与无损压缩　　1.1 度量信息　　信息论的奠基人香农在信息论中第一次用数学的方式量化了信息的大小。　　假设有一个信息生成器
，
产生的符号来自集合
${\mathcal{S}}=\{s_1,s_2,\cdots,s_m\}$ 。信息生成器
生成每个字符的概率为
。信息生成器
的信息量定义为
H(X) ，中文名叫信息熵。
H(X) 的计算公式如下：　　
$H(X) = -\sum_{s\in {\mathcal{S}}}p(x=s) \log_2 p(x=s) \tag{1}$ 下面举一个实际的例子帮助读者理解：　　对于信息生成器
，我们指定集合
$\mathcal{S} = \{a,b,c,d,e,f\}$ 。每个符号产生的概率
p(x) 如下：　　
$\begin{aligned} p(x=a) = \frac{3}{11} \\ p(x=b) = \frac{3}{11} \\ p(x=c) = \frac{2}{11} \\ p(x=d) = \frac{1}{11} \\ p(x=e) = \frac{2}{11} \end{aligned}\tag{2}$ 　　现在，我们可以使用信息熵的公式
(1) 计算
的熵：　　
$\begin{aligned} H(X) &= - \sum_{s\in S} p(x=s) * \log_2(p(x=s)) \\ &= - (\frac{3}{11}\log_2 \frac{3}{11}+\frac{3}{11} \log_2 \frac{3}{11} +\frac{2}{11}\log_2 \frac{2}{11}+\frac{1}{11} \log_2 \frac{1}{11} + \frac{2}{11}\log_2 \frac{2}{11}) \\ &\approx 2.2313 \end{aligned}\tag{3}$ 　　请读者牢记上面的例子，上面的信号生成器
在后面还会看到。　　现在我们已经学会了熵的计算，但熵的定义似乎太抽象了。熵有什么具体的物理含义吗？　　1.2 熵与编码　　细心的读者会发现，我们在定义熵的时候选择
作为
$\log$ 的底。为什么要选择
为底呢？　　因为在计算机中，我们一般用二进制来进行数据的存储与传输，也就是用
和
来表示一切的信息。　　现在来考虑这样的一个问题，假设对于信号生成器
，我们需要通过计算机的二进制编码来传递
生成的信息，也就是用类似于
$010111\cdots$ 这样的
比特流。注意信息生成器
可以生成无穷条长度有限的字符串（信息）。　　一个简单的想法是通过定长的
编码实现这个功能。　　对于信号生成器
，我们设计如下的编码表：
$a \to 000$
$b \to 001$
$c \to 010$
$d \to 011$
$e \to 100$ 　　假设我们要传递信息为。信息发送方先将信息编码为。接着将编码后的比特流传输出去。信息接收方接受到信息后，按照固定长度
进行切分，再通过上面的编码表反向解码成。　　发送
个符号，一共付出了
个二进位的代价，在这条消息中，平均每个字符的编码长度为
。需要注意的是，信息生成器
可以生成无穷条长度有限的信息，每一条信息都可以用上面的编码方式进行编码。不难计算出信息生成器
平均每个字符的编码长度也是
。　　定长的编码方式并不是最优的编码方式，因为不同的字符，它们出现的概率是不同的。为了使得传递信息的编码长度尽量的短（提升信息传递的效率），我们应该使用如下的原则进行编码：字符出现的概率越大，则对应编码应该越短，反之则越长。　　通过这样的原则产生的编码是不定长的编码。然而不定长的编码的构造并不简单。因为不定长的编码存在一个问题：如何保证传递的信息能没有歧义的进行切分和解码。　　定长的编码可以根据固定的长度进行切分，从而保证传递信息在解码的时候不存在歧义。而不定长的编码如果要保证编码后的信息在解码阶段不产生歧义，就得要求任意一个字符的编码不能为其他字符编码的前缀，这种性质的编码称为前缀码。例如下面的编码表是不满足前缀码的编码表：
$a \to 00$
$b \to 01$
$c \to 10$
$d \to 101$
$e \to 11$ 　　的编码是的编码前缀，在解码时，无法判断应该解码成还是，解码阶段出现了歧义。　　下面我们直接将给出一个满足前缀码要求的编码表。　　对于信息生成器
，根据它的概率
，设计如下的满足前缀码要求的编码表：
$a \to 00$
$b \to 01$
$c \to 10$
$d \to 110$
$e \to 111$ 　　不难看到，上面的编码表满足没有歧义的要求。根据上面的编码表，信息可被编码成如下的比特流：。
个字符，一共付出了
个二进位的代价，在这条消息中，平均每个字符的编码长度约为
2.2727 。同样需要注意的是，信息生成器
可以生成无穷条长度有限的信息，每一条信息都可以用上面的编码方式得到一个长度。接下来我们来计算信息生成器
每个符号的平均编码长度：　　
$\begin{aligned} 信息发生器 X 的平均编码长度 &= \sum_{s\in {\mathcal{S}}} p(x=s)l(s)\\ &=2\frac{3}{11}+2\frac{3}{11}+2\frac{2}{11}+3\frac{1}{11}+3\frac{2}{11}\\ &\approx 2.2727 \end{aligned}\tag{4}$ 　　在后文中，我们用平均编码长度表示信息发生器
每个符号的平均编码长度。　　实际上，上面的这种编码方式称为哈夫曼编码。这是一种很著名的不定长编码方法。需要注意的是，当我们已知各个字符出现的概率
时，哈夫曼编码的编码表可以通过特定的算法（程序）生成。除此以外，解码阶段也需要编码表才能顺利的解码，所以我们常将编码表或者概率
作为信息放入发送的比特流中。由于哈夫曼编码的资料非常好找，我们就不再赘述哈夫曼编码的编码表是如何根据概率
生成的了。这里请读者自行查找相关资料学习。　　关于哈夫曼编码，有以下的数学事实：　　假设字符
s_i 生成的概率为
p_i ，那么该字符的哈夫曼编码长度满足下面不等式：
$l_h(s_i) \leq\lceil -\log_2 p_i \rceil \tag{5}$ 其中
表示字符
s_i 的哈夫曼编码长度，
$\lceil \cdot \rceil$ 表示向上取整。关于证明的详细资料可以参考《T. M. Cover and J. A. Thomas, Elements of Information Theory, vol. 2. John Wiley & Sons, 2006. 》。　　前面我们通过改变编码的方式缩小了平均编码的长度。那能否通过不断的改进编码，让平均编码长度越来越小呢？　　答案是否定的，香农通过数学理论证明了平均编码长度的下限就是信号生成器
的熵，换句话说：熵代表了对信息编码所需要的最短平均编码长度　　这正是熵的物理含义。　　对于上文中的信息生成器
，它的平均编码长度的极限约为
2.2313 。　　为什么哈夫曼编码无法达到熵的极限呢？其实这个很好解释。原因每个字符的编码长度只能是整数，无法取到小数。在前面的例子里，字符
和
生成的概率并不同，但它们的编码长度却相同，这正是由于编码长度的四舍五入所导致的。　　那有没有比哈夫曼编码更优的编码方法，使得编码长度更加逼近
H(X) 呢？答案是有的，这种编码方式称为算术编码。　　1.3 算术编码　　通过对哈夫曼编码的分析，不难发现，无论如何设计不定长的编码表，都无法避免编码长度只能为整数的缺陷。算术编码通过巧妙的设计，规避了这个问题。不定长编码是通过编码表，将一个个字符映射逐个映射成对应的编码。算术编码则是对整个字符串进行编码。　　为了方便描述算术编码和解码的过程，我们缩短传递信息的长度。假设要传递的信息为。　　首先，我们根据信息生成器
每个字符的生成概率
，将
[0,1] 区间按照对应的概率比值
划分为下面的样子(注意，后面为了方便书写，统一只保留了三位小数，实际计算中需要根据要求保留对应的精度)：

　　信息的第一个字符为
，于是将上图对应的第二段拿出来，然后再次根据
的比例将区间
划分为下面的样子：

　　信息的第二个字符为
，于是将上图对应的第一段拿出来，再次根据
的比例将区间
划分为下面的样子：

　　最后一个字符为
，我们将上面的第二段取出。在这段区间内，寻找一个二进制最短的小数。寻找的过程如下：将
[0,1] 区间二等分为
[0,0.5] 和
[0.5,1] 。
在
[0,0.5] 区间内。选择
[0,0.5] 区间。将
[0,0.5] 二等分为
和
。
在
区间内。选择
区间。将
二等分为
和
。
在
区间内。选择
区间。
的中间值
0.3125 在区间
。
0.3125 就是我们要找的指定区间内二进制最短的小数。　　不难发现，这本质上是二分查找算法，它正是对应着将十进制转成二进制小数的过程。最终我们有：　　
$(0.0101)_2 = (0.3125)_{10} \tag{6}$ 　　需要注意的是，这种方法的二进制小数最后一位一定为 1 。所以我们在传递信息的时候只需要传递
010 即可。信息接受方接受到
010 后，在后面加上
，在前面加上
，就能得到完整的值
。　　如何解码呢？信息接受方先将
转换为十进制小数，即
0.3125 。除此外，信息接收方还会接受到信息生成器
每个字符的生成概率
，接着将
[0,1] 区间按照对应的概率比值
划分为下面的样子：

　　
0.3125 在上图的第二个区间内，所以第一个解码字符是
。然后将第二个区间继续按照
的比例划分：

　　
0.3125 在上图的第一个区间内，所以第二个解码字符是
。然后将第一个区间继续按照
的比例划分：

　　
0.3125 在上图的第二个区间内，所以最后一个字符是
。最终得到解码信息。　　如果使用哈夫曼编码，传递需要 6 位二进制位，而算术编码只需要 3 位。　　下面我们同样给出一些算术编码的理论结果，这些结果是通过数学严格推导出来的。具体证明细节可以参考书籍《G. E. Blelloch, Introduction to Data Compression. Carnegie Mellon University, 2013.》　　事实一：　　假设信息生成器
生成长度为
的信息
x_n 。
x_n 的算术编码长度满足如下关系：　　
$l_a(x_n) < \lceil -\log_2 p(x_n) \rceil +1 \tag{7}$ 　　其中
表示字符串
x_n 的算术编码长度。
p(x_n) 表示字符串
x_n 被生成的概率。
$\lceil \cdot \rceil$ 表示向上取整。　　事实二：　　如果我们不知道信息生成器
的概率分布
怎么办？实际上，我们可以使用任意离散的概率分布
来对
的信息编码和解码。例如：　　
$\begin{aligned} q(x=a) = 0.2 \\ q(x=b) = 0.2 \\ q(x=c) = 0.2 \\ q(x=d) = 0.2 \\ q(x=e) = 0.2 \end{aligned}\tag{8}$ 　　如果我们用概率分布
对
的信息进行算术编码，我们可以计算出它的平均编码长度满足下面的关系：　　
$\begin{aligned} 平均编码长度 &\leq -\sum_{s\in {\mathcal{S}}}p(x=s)\log_2 q(x=s) +2 \\ &= H(p,q)+2 \end{aligned}\tag{9}$ 　　熟悉深度神经网络和信息论的读者不难看到，
H(p,q) 正是我们常用的交叉熵。公式
(9) 告诉我们，如果你用的分布
和分布
越接近，你算术编码的平均编码长度就越短！　　事实三：　　随着信息长度的增加，算术编码的平均编码长度会不断趋近于信息的熵极限。　　讲解完上面三个事实后，我们再来总结一下哈夫曼编码和算术编码：哈夫曼编码是对信息的每一个字符逐步编码。算术编码是对整条信息编码。哈夫曼编码可以生成编码表，编码表由概率
通过特定的算法生成，解码也需要编码表，所以本质上哈夫曼编码除了传输编码信息还需要传输概率
。算术编码没有编码表的概念，但算术编码同样需要传输概率
。算术编码在理论上比哈夫曼编码更加靠近熵极限。随着编码信息量的增加，算术编码会不断趋近于信息的熵极限。　　最后关于算术编码，我们其实一直忽略了一个非常重要的问题，这个问题导致了很多人误解了 OpenAI 关于压缩即智能思想的一些关键步骤。信息接受者如何感知到什么时候停止解码？例如在前面的例子中，算术编码对应的十进制小数是
0.3125 。我们既可以将它解码成，也可以将它解码成，甚至能继续无限的解码下去。　　对于这个问题，我们有三种解决方案。　　方案一是信息发送者和接受者约定好信息的发送长度。例如约定发送的信息长度只为
。那么接受者接收到算术编码后只解码
次。　　方案二是字典表
$\mathcal{S}$ 中有一个特殊的字符表示结束，例如
$\mathcal{S} = \{a,b,c,d,e,f\}$ ，其中
表示结束。当接受者解码信息到
时就会结束解码。　　方案三是在算术编码的比特流前加入一个固定长度的信息，这个信息表示的是后续算术编码的解码次数。　　首先，方案一是不合理的，因为每次只对一个(或多个)字符进行算术编码并没有发挥算术编码的优势，算术编码应该是对整条信息编码。除此外，如果使用这种方法，接受者接受比特流的时候无法判定什么时候这一段字符的编码到底了，这意味需要付出更多的信息代价来表示每段字符的开始和结束。目前互联网上对 OpenAI 压缩智能的解读都是用的这个思路，这个思路是完全错误的。　　其次，方案二也是不合理的，因为我们控制结束字符出现的位置，很可能结束字符在信息的中间就会出现，如果是这样就意味着我们要把信息拆解成几部分然后发送出去。那么这种情况其实和方案一是类似的，这意味着我们需要付出更多的信息代价来区分不同段的算术编码，而且不对整条信息编码也无法发挥算术编码的优势。　　所以我们真正使用的是方案三，我们先用算术编码将整段信息全部编码，然后在算术编码的比特流前加入一个固定长度的信息，这个信息表示的是后续算术编码的解码次数。固定的长度信息相比要解码的次数是微不足道的。例如对于小于
$2^{128}$ 次解码，我们只需要保留
128 个二进位表示解码的次数（不足
128 位的，前面用
补全）。　　1.4 动态编码　　前一小节我们提到的算术编码其实是静态的编码。所谓静态编码是指信息发生器
的概率分布
在信息生成的过程中不会发生任何变化。实际上，我们可以动态的调整概率分布
。例如生成第
个字符的概率分布是
p_1 ，生成第
个字符的概率分布是
p_2 ，
$\cdots$ ，生成第
个字符的概率分布是
p_t 。　　虽然
是动态变化的，但我们仍然能使用算术编码进行编码和解码。接下来，我们以一个具体的例子来说明这个过程：　　假设我们要编码的信息是。　　此时
$p_1 = (\frac{3}{11},\frac{3}{11},\frac{2}{11},\frac{1}{11},\frac{2}{11})$ ，将
[0,1] 区间按照概率比例划分成下面样子：

　　信息的第一个字符是
，我们选择上图中的第二段。此时的概率变成
，将
区间按照概率比例划分成下面的样子：

　　信息的第二个字符是
，我们选择上图中的第一段。此时的概率又变成了
，将
区间按照概率比例划分成下面的样子：

　　最后一个信息的字符为
，将上面的第二段取出。在这段区间内，寻找一个二进制最短的小数。　　
$(0.01001)_2 = (0.28125)_{10} \tag{10}$ 　　解码过程和静态算术编码的解码过程是类似的，这里就不再赘述。需要注意的是，解码的时候除了需要知道算术编码信息
外，还需要知道概率
以及解码的次数。　　
是怎么来的呢？聪明的读者可能已经想到了，可以用深度神经网络来进行预测。这就是 OpenAI 压缩即智能思想的本质。　　等等，难道只能用算术编码进行动态编码吗？答案是否定的，哈夫曼编码也能做动态编码！哈夫曼编码的编码表是通过
产生的，我们只需要每次根据变动的
调整哈夫曼编码表就能实现动态的哈夫曼编码！关于动态哈夫曼编码这里就不再赘述了。　　1.5 无损压缩　　前面的四个小节中，我们简要介绍了哈夫曼编码、静态算术编码、动态算术编码和动态哈夫曼编码。这些编码技术的共同目标是将原始信息（我们将定长编码视为原始信息）压缩成更短的形式。这种压缩是无损的，因为我们始终能够通过解码将编码后的信息准确、无歧义地还原为原始信息，而不会引入任何错误。　　无损压缩有
个关键的模块和结果：原始信息。（需要压缩的信息）压缩算法。（压缩信息的方法）压缩信息。（压缩后的信息）解压算法。（解压信息的方法）　　然而，香农定义的熵似乎给我们压缩的下限判了死刑。实际上信息的无损压缩是可以突破熵的极限的。因为熵的定义只考虑了符号出现的概率，它并没有考虑到符号之间的「顺序」和「关系」。　　下面举一个简单的例子方便读者理解：　　信息生成器
生成了以下两条信息：
$bdeaebcaabc \\ aaabbbccdee \tag{11}$ 这两条信息生成的概率是相同的。它们的编码长度也是一样的。但对于第二条信息，它还额外包含了排序的信息（「顺序」）。　　关于为什么能突破熵的极限，我们在分析完 OpenAI 压缩即智能的思想后，我们会进一步的展开。　　二、自回归与无损压缩　　2.1 基本符号　　将神经网络中的自回归模型用到无损压缩中并不是 OpenAI 的首创。实际上，天才程序员 Fabrice Bellard 于 2019 年就已经开源了一个用自回归模型对数据进行无损压缩的工具 NNCP。它的思想更是可以追溯到 2011 年的论文《A Machine Learning Perspective on Predictive Coding with PAQ》。　　但 OpenAI 将大模型的训练过程和无损压缩划上等号仍然是划时代性的，一方面他们认为智能的程度可以用压缩率指标来量化，智能只是无损压缩过程中的一个副产品而已。另一方面在无损压缩的视角下，模型的参数量根本不重要，这使得 OpenAI 敢于不断的增加模型的参数量，直至出现了 ChatGPT 这样现象级的产品。　　我们先来定义一些基本符号，方便后面的描述。　　假设我们有一串原始信息（这里特指文本）记为
$\mathcal{D}$ ，
$\mathcal{D}=[s_0,x_1,x_2,x_3,\cdots,x_n]$ ，
s_0 是一个特殊的字符，表示原始信息的开始。
x_i 表示原始信息中每一个，关于更多的内容可以参考这篇文章。
x_i 来自一个有限的集合
$\mathcal{S}$ 。需要注意的是，
是特别大的，例如用的
$\mathcal{D}$ 大概有 3000 亿个，集合
$\mathcal{S}$ 的大小大概是 5 万多。　　我们将自回归模型记为
，
$\theta_t$ 表示自回归模型在第
时刻的参数。那么对第
t+1 个预测的概率可表示成下面的公式：
$p_{t+1} = f(x_{t+1}\vert s_0,x_1,x_2,\cdots,x_{t} ;\theta_t) \tag{12}$ 　　其中
$p_{t+1}$ 表示自回归模型对第
t+1 个的预测，这是一个离散的分布。　　自回归模型
的代码（例如模型的训练代码）和各种随机种子（例如各种参数的初始化等）打包成一个信息。这个信息我们记为
。　　一切准备就绪，接下来开始正式介绍如何用自回归模型
进行无损压缩。　　2.2 压缩过程　　信息发送方根据
执行代码，初始化神经网络参数
$\theta_0$ 。第
时刻，执行
$f(x_1 \vert s_0 ;\theta_0)$ 。输出对第
个的预测概率
p_1 。第
时刻，我们用
p_1 对字符
x_1 进行算术编码。注意，
x_1 真实的概率分布
p_1 是未知的，但从 1.3 小节的内容中，我们知道用
p_1 对
x_1 也是可以进行算术编码的。注意，此时的算术编码刚开始第一次区间划分，然后根据
x_1 选择了一个区间。我们记这个区间为
。第
时刻，根据真实的
x_1 和预测的
p_1 进行反向传播，更新
的参数，得到
$\theta_1$ 。第
时刻，执行
$f(x_2 \vert s_0,x_1;\theta_1)$ 。输出对第
个的预测概率
p_2 。第
时刻，我们用
p_2 对字符
x_2 进行算术编码。注意，此时的算术编码在
的基础上进行第二次区间划分，然后根据
x_2 选择了一个区间。我们记这个区间为
。不难看到，整个算数编码是持续进行下去的，区间在不断的划分，但每次划分使用的概率
p_t 是变化的，所以这是使用的 1.4 小节中的动态算术编码。第
时刻，根据真实的
x_2 和预测的
p_2 进行反向传播，更新
的参数，得到
$\theta_2$ 。　　我们不断的重复步骤
至步骤
，直到第
n-1 时刻。最终我们将得到一个区间
$[l_{n},r_{n}]$ 和参数
$\theta_{n}$ 。我们选择
$[l_{n},r_{n}]$ 内二进制最短的小数
z_n 作为整段信息
$\mathcal{D}$ 的算术编码。　　以上就是压缩的整个过程。　　压缩后的信息由三部分组成：算术编码
z_n (去掉小数点前的 0 和尾部的 1)代码信息
。需要解码的次数信息。这里我们用
表示。　　等等，模型的参数
$\theta_n$ 呢？难道这个不是压缩后的信息吗？难道解压不需要模型参数吗？这正是用自回归模型做无损压缩最神奇的地方，我们真的不需要模型的参数就能完美的解压。　　2.2 解压过程　　信息发送方将压缩后的三部分信息通过比特流发送给信息接受方。信息接受方现在开始解码。　　信息接受方根据
执行代码，初始化神经网络参数
$\theta_0$ 。注意，由于
中包含了各类随机种子的信息，所以这里的
$\theta_0$ 和 2.2 中的
$\theta_0$ 是一模一样的。第
时刻，执行
$f(x_1 \vert s_0 ;\theta_0)$ 。输出对第
个的预测概率
p_1 。第
时刻，根据
p_1 和接受到的
z_n 进行算术解码。解码的过程是根据
p_1 做第一次区间划分。信息接受方会发现
z_n 在
这个区间内。于是解码出第一个
x_1 。注意这一步是无损的，一定能百分百解码准确，这是由算术编码的数学理论保证的。第
时刻，根据解码出的
x_1 和预测的
p_1 进行反向传播，更新
的参数，得到
$\theta_1$ 。注意，由于信息发送方和信息接受方各种随机种子完全一致。这里的
$\theta_1$ 和 2.2 中
$\theta_1$ 是一模一样的。第
时刻，执行
$f(x_2 \vert s_0,x_1 ;\theta_1)$ 。输出对第
的预测概率
p_2 。第
时刻，根据
p_2 和接受到的
z_n 进行算术解码，解码出第二个
x_2 。解码的过程是将
根据
p_2 做第二次区间划分。信息接受方会发现
z_n 在
这个区间内。于是解码出第二个
x_2 。第
时刻，根据解码出的
x_2 和预测的
p_2 进行反向传播，更新
的参数，得到
$\theta_2$ 。　　我们不断的重复步骤
至步骤
，直到第
n-1 时刻（
n-1 是读取信息
得到的）。最终我们将
z_n 无损的解码成了原始信息
$\mathcal{D}$ 。不难发现，整个解码过程并没有事先传递模型的参数
$\theta_n$ 。　　请读者仔细回顾一下压缩的过程和解压的过程。不难发现，其实我们可以不用动态算术编码进行编码和解码，使用动态的哈夫曼编码也是可以的！使用动态的哈夫曼编码的唯一缺陷是它编码后的编码长度理论上比算术编码更长一点。需要注意的是，动态的哈夫曼编码是一个一个的编码字符，和动态算术编码对整个信息编码不一样。　　2.3 计算压缩率　　回顾 1.3 小节的事实二：　　如果我们用概率分布
对
的信息进行算术编码，我们可以计算出它的平均编码长度满足下面的关系：　　
$\begin{aligned} 平均编码长度 &\leq -\sum_{s\in {\mathcal{S}}}p(x=s)\log_2 q(x=s) +2 \\ &= H(p,q)+2 \end{aligned}\tag{13}$ 　　其中
是
的真实分布。我们将这个结论用于我们计算压缩率。　　压缩率的计算难点在于估计
$\vert z_n \vert$ 的编码长度。　　对于数据集
$\mathcal{D}$ ，我们用
${\hat p}_{t}$ 表示它在自回归建模中的真实分布：　　
${\hat p}_{t} = p(x_t\vert s_0,x_1,x_2,\cdots,x_{t-1}) \tag{14}$ 　　注意，这里的真实分布
${\hat p}_{t}$ 其实是一个独热编码。因为
${\hat p}_{t}$ 在数据集
$\mathcal{D}$ 中是一个确定的。　　根据前面的事实二，压缩后信息的算术编码
z_n 的平均编码长度满足如下的关系：　　
$\begin{aligned} z_n 的平均编码长度 &\leq \frac{1}{n}(2n+\sum_{t=1}^nH({\hat p}_{t},p_{t}))\\ &= 2+ \frac{1}{n}\sum_{t=1}^nH({\hat p}_{t},p_{t}) \\ &= 2+\frac{1}{n}\sum_{t=1}^n\log_2 p^*_t \end{aligned} \tag{15}$ 　　这里
p_t^* 不再是向量，而是一个值。举一个例子方便读者理解，假设预测的
，
${\hat p}_t = (0,1,0)$ 。那么
。　　压缩后信息的
$\vert F\vert$ 和
$\vert d \vert$ 是基本固定的，相比
$\vert z_n \vert$ 也是微乎其微的。为了尽量的压缩信息，就需要尽量的减少
z_n 的平均编码长度。直接减少
z_n 比较困难，由于我们有
z_n 的上界，我们可以转而去减少
z_n 的上界，即：　　
$\min \frac{1}{n}\sum_{t=1}^n\log_2 p_t^*\tag{16}$ 　　熟悉自回归建模的读者会惊奇的发现，上面的优化目标正是自回归模型训练的损失函数！　　于是，我们可以将训练过程中的损失函数画图画出来。图的横轴是已训练的步数（或者已训练的 token 数，两者是等价的），纵轴是公式
(16) 。

　　如果看单条曲线，上面的图告诉我们，随着压缩的进行，压缩的效率越来越高。平均编码长度越来越小！　　如果看多条曲线，上面的图告诉我们，曲线下的面积越小，说明
z_n 的平均编码长度的上界越小，说明压缩率越高！　　最后我们看一下自回归模型做无损压缩的压缩效率有多高。下图是 OpenAI 工程师 Jack Rae 在一次分享中的截图。

　　从上图可以看到，LLM 的无损压缩效率是远远超过目前市面上最好的压缩器的，这是为什么呢？Jack Rae 认为，这是因为 LLM 已经具备了智能。　　（最好压缩器是 8.7 倍压缩率，LLM 能达到至少 14 倍，这还是比较一般的 LLM 模型）　　2.4 更多的启示　　截止目前为止，我们已经严格的证明了自回归模型的训练过程等价于无损压缩。这个新的视角对我们有什么启示呢？　　第一点：　　自回归模型等价于无损压缩是在理论上有保证的，这可能是 OpenAI 为什么一直坚持 next token prediction 训练范式的原因之一。　　第二点：　　OpenAI 认为能用压缩率来统一量化不同参数量，不同结构的模型的智能程度。注意，在无损压缩的视角下，模型的参数数量是不重要的，因为不同大小的模型的
$\vert F\vert$ 的大小是基本一样的。例如一个模型是
层，另一个模型是
100 层。后者只需要把
中的一个参数修改一下即可，带来的信息量的变化和其他部分相比微乎其微。　　第三点：　　这是一种完全不同的看待泛化的角度。在以前，机器学习中的奥卡姆剃刀原则是需要考虑模型的参数量的。一直以来，学术界很难解释为什么参数量如此大的神经网络泛化效果这么的好，这是非常的反直觉的。而前面的无损压缩理论告诉我们，压缩和模型的参数根本没有关系。而且无损压缩仍然满足奥卡姆剃刀原则，即用最少的编码信息去表示原始的信息。　　第四点：　　既然无损压缩效果与模型的参数量无关，为了增加模型的压缩率，不断增加模型的参数量似乎是最直接、最简单的选择。这也许是 OpenAI 从一开始就选择了不断增加参数这条路的核心原因之一。　　第五点：　　在无损压缩的视角里，无论是压缩还是解压，我们只需要训练一个，也就是遍历数据一遍。在这个视角下，模型每一次的 next token prediction 都是对未曾见过的数据进行预测（前提是数据质量比较高，没有明显的重复数据）。目前大部分的大型语言模型的确只训练 1 个左右的。　　第六点：　　神经网络
$f(\theta_n)$ 是无损压缩过程中的副产品。这个副产品可能是具有智能的。这也是 OpenAI 为什么宣称无损压缩是通向 AGI 的一条可能路径之一。　　第七点：　　无损压缩的数据
$\mathcal{D}$ 非常重要，我们需要数据量足够大的且有效的数据。这里的有效可能是指包含有足够的「人类知识」的数据。OpenAI 在
$\mathcal{D}$ 上一定是花了不少功夫的。前段时间的一篇论文《Textbooks Are All You Need》说明，即使是包含有足够知识的小数量，也能达到不错的效果。这变相说明了数据质量的重要性。　　第八点：　　OpenAI 认为，无损压缩可以进一步推广到更广义的无损压缩。举个例子，笔者脑子里可能记得《七龙珠》这部动漫，但当有人问我一些动漫的细节时，我不一定能完全记起来，但我知道如何通过相关的工具，例如搜索引擎来查询到我想要的信息。所以合理的使用外部工具也是一种广义的无损压缩。这也是为什么 GPT 在前期推出了插件系统，在最近又推出了 function calling 功能，这都是在赋予 GPT 使用外部工具的能力。根据 OpenAI 的官方文档，function calling 功能并不是类似于 ReAct 或是 self-ask 那样的上下文学习，它是模型微调的结果，所以有理由相信，OpenAI 可能已经实现了如何将外部工具的使用也纳入到无损压缩这套理论框架之中。　　三、无损压缩的极限　　3.1 突破信息熵的极限　　让我们回到 1.5 小节的内容。熵仅仅是独立同分布下的信息编码的下限。很多真实的数据并不是独立同分布的，这也给了我们突破熵的极限的希望。　　毫无疑问，GPT 一定是突破了香农熵的极限的。原因是因为 GPT 掌握了数据集
$\mathcal{D}$ 生成的规律。　　那什么是数据生成的规律呢？为什么数据的生成和智能可能有联系呢？让我们用极限的思维思考一个极端的例子。我们有圆周率
$\pi$ 小数点后 100 亿位的数字。如何对这 100 亿位数字进行无损压缩？　　在香农的视角里，我们无法对
$\pi$ 进行无损压缩。因为
$\pi$ 是正规数（实际上这个结论并没有在数学上被证明，但至少前
100 亿位数，小数部分每个数字出现的概率是近乎相等的）。所以
$\pi$ 的每一个数字出现的概率都是
0.1 。这导致我们只能使用定长的编码来保存
$\pi$ 的每一位数字而没有任何的优化空间。　　但是真的是这样吗？　　实际上，我们如果知道了
$\pi$ 的含义（圆周处以直径），有足够的数学知识。我们完全可以设计一个程序算法来动态的生成
$\pi$ 的任意位数的小数。例如高斯-勒让德算法，它的程序仅仅几十行：

　　如果我们有近乎无穷的计算资源和时间，我们可以轻易的把
$\pi$ 压缩成一段几十行的程序，而它的编码长度必然会远远小于 100 亿位。只是解压的时间稍微有亿点点长。　　所以
$\pi$ 这个例子告诉我们，我们可以突破熵的极限，有时候突破熵的极限需要我们有知识，甚至智能。　　即然熵并不是无损压缩的极限，那么无损压缩的极限到底是什么呢？　　3.2 柯氏复杂度　　让我们把 3.1 小节的内容进行延伸，我们引入一种新的度量信息的方式，它称为柯氏复杂度。　　柯氏复杂度是算法信息论中的内容，算法信息论是一门将信息论，可计算理论和概率论结合起来的学科。　　假设我们有信息
。
是一个通用图灵机，不了解通用图灵机的读者可以简单的把它认为是一个可编程的通用计算机。我们在
上写的程序记为
。
K_U(x) 表示信息
在
上的柯氏复杂度，它的数学表达式如下：　　
$K_U(x) = \min \{l(p): U(p)=x\} \tag{17}$ 　　其中
l(p) 表示程序
的长度。
U(p) 表示程序在图灵机上运行的结果。那么
K_U(x) 就是要找一个在图灵机
上能生成
的最短的程序。换句话说，我们要在
上找一个最短的描述
，
能生成
，
K_U(x) 就是这个最短描述的长度。　　为什么要加下标
呢？因为在不同的图灵机下描述信息
的长度是不一样的。例如你有一台运行语言的计算机，也有一台运行的计算机，那么显然完成相同的目的，比如打印需要的程序编码长度是不一样的。　　下面我将介绍柯氏复杂度很有趣的性质，这个性质是后面推导的基础。　　假设我们有两台通用图灵机
和
（读者可以简单理解为一台运行的计算机，一台是运行的计算机）。如果我们有同一个信息
。
K_U(x) 和
K_V(x) 有什么关系呢？　　在算法信息论中，我们可以证明：
$K_U(x) \leq K_V(x)+C_{U,V} \quad \forall x\tag{18}$
$C_{U,V}$ 是一个和
U,V 有关，但是和信息
无关的常数。我用白话解释一下这个公式，对于任意的程序
，它既可以被编程语言 1 (例如 )实现，也可以被编程语言 2(例如)实现，实现它们的最短描述长度只差一个常数，这个常数是固定的，与程序
无关，只和你选择的编程语言有关。由于
$C_{U,V}$ 是和信息
无关的数，所以公式
(18) 又常会写成下面的样子：　　
$K_U(x) \leq K_V(x)+O(1)\tag{19}$ 　　关于
(18) 的证明，可以参考这篇文章。从柯氏复杂度的定义不难看出，它就是我们要找的无损压缩的极限！　　遗憾的是，Berry 悖论告诉我们，柯氏复杂度
K_U(x) 是不可计算的（详细证明过程可以参考链接）。不可计算意味着在图灵机上，不存在一个程序，它把任意字符串
作为输入，然后输出它的
K_U(s) 。目前我们已知的任何计算设备都无法超越图灵机。　　即然柯氏复杂度不可计算，是一个我们无法在图灵机上达到的目标，那它对我们有什么意义呢？　　柯氏复杂度很可能就是智能的体现，请读者回想 3.1 小节的例子。　　如果存在一个函数，它可以计算出任意信息的最短描述，毫无疑问，它一定是一个超智能体！　　3.3 逼近柯氏复杂度　　假设我们有一个可计算的无损压缩器
C_V (注意这里是无损压缩器，不是常数)，
C_V 表示无损压缩器
运行在通用图灵机
上。　　对任意的信息
，如下不等式成立：　　
$K_U(x) < \vert C_V(x) \vert + K_U(C_V)+O(1) \quad \forall x \tag{20}$ 　　
C_V(x) 表示在图灵机
上运行压缩器，对信息
做无损压缩。
$\vert C_V(x)\vert$ 表示信息压缩后的长度。
表示在图灵机
上描述
C_V 的最短描述。
O(1) 表示和信息长度
无关的常量。　　这个不等式的证明是非常简单的，首先如下公式成立：　　
$K_U(x) < K_V(x)+O(1) \quad \forall x \tag{21}$ 　　
K_V(x) 一定是小于
$\vert C_V(x) \vert +\vert C_V \vert$ 。这里
$\vert C_V \vert$ 表示压缩器
在图灵机
上的描述长度（例如某程序在解释器的代码长度）。但这个上界并不是最优上界，我们可以用图灵机
来描述
C_V 。于是有：
$K_V(x)<\vert C_V(x) \vert+K_U(C_V) +O(1) \tag{22}$ 公式
(21) 和
(22) 组合到一起可得公式
(20) 成立。　　我们将自回归模型的无损压缩过程和上面的公式
(20) 做对比。我们会惊奇的发现
C_V 就是我们用自回归模型实现的无损压缩器（包括算术编码），如果说的再详细一点，
是我们目前用的计算机（一种通用图灵机），
C_V 是我们在计算机上实现的自回归模型和算术编码。我们把
C_V 固定，当我们在遍历所有信息
进行压缩(但不可能所有的信息)的时候，右边的最短描述长度在不断的逼近柯氏复杂度
K_U(x) ！LLM 的训练过程就是在向柯氏复杂度（超智能体）前进！　　遗憾的是，我们无法知道这样的逼近距离
K_U(x) 到底有多近。　　根据 Chaitin 定理（不可能编程判断代码的最简性），我们甚至无法知道什么时候逼近到达极限（不可能编程判断代码的最简性）。　　由此，这会延伸出几个无法给出答案的问题，这些问题恐怕只能在哲学层面上讨论了：如果无损压缩真的能实现通用人工智能，那么需要多接近无损压缩极限才能达到通用人工智能呢？如果是要达到柯式复杂度才能实现通用人工智能，这是否意味着智能不是图灵可计算的？换句话说，仅通过图灵机（计算机）能实现人工智能吗？有没有可能在这套理论下，我们在无限的逼近 AGI（每次比上一次更加的强大），但永远又到不了 AGI？（就好比神经网络的对抗攻击，永远无法避免）　　作为从业者，屁股决定脑袋。　　笔者只能乐观地认为，当无损压缩达到一定下限时，就会出现通用人工智能（AGI），智能是图灵机可以模拟计算的。　　3.4 条件柯氏复杂度和上下文学习　　这一小节是对 Ilya Sutskever 对条件柯氏复杂度和无监督学习关系的一点个人解读，不太准确，可暂时忽略。　　在第二章中，我们强调了数据
$\mathcal{D}$ 的重要性。对于语言模型，
$\mathcal{D}$ 必然代表的是各种各样的文本信息。从机器学习的角度上看，这些文本信息都是没有标签的。但是真的如此吗？　　为了方便读者理解，我以文本分类中的情感分类问题为例。在情感分类问题中，我们想学习一个模型，该模型根据文本
判断文本的类别
是高兴，伤心，还是中性。在传统机器学习中我们会将标签类别用独热编码表示。　　然而，高兴，伤心以及中性这些词汇本身在自然语言中就是有含义的。换句话说，自然语言的标签
就是自然语言的一部分，我们不应该将它和文本
剥离开来。　　因此，从这个视角上来看，
$\mathcal{D}$ 是即包含了
也包含了
。需要注意的是，
的种类是非常多的（不一定是前面说的分类问题）。
和
相互之间也可能有交集。因此
和
是你中有我，我中有你。　　因此，对于前文提到的对
$K_U(\mathcal{D})$ 的逼近，本质上可以写成对
的逼近。根据《The complexity of finite objects and the development of the concepts of information and randomness by means of the theory of algorithms. 》，
可以写成如下的形式：　　
$K_U(X,Y) = K_U(X)+K_U(Y\vert X)+O(\log(K_U(X,Y))) \tag{18}$ 　　其中
$K_U(Y\vert X)$ 表示条件柯氏复杂度，表示在已知信息
的情况下，描述
的最短长度。上面公式说明，能够输出
和
的最短程序，相当于输出
和已知
的情况下可以输出
的程序之和再加上一个对数参数。　　因此，对
X,Y 做联合压缩，可能能得到近似
$K_U(Y\vert X)$ 这个副产品。直接去近似
$K_U(Y\vert X)$ 是不可行的，因为目前无法做到让整个数据集作为条件进行压缩。除此外，你无法针对不同的
去计算近似不同的
$K_U(Y\vert X)$ ，因为关心的
太多了。例如不同的文本分类，不同的命令实体识别等等。一起压缩可能能拿到一个通用的
$K_U(Y\vert X)$ 。　　需要注意的是，
$K_U(Y\vert X)$ 需要和
K_U(X) 配合使用。即先生成
，然后生成
。前面提到，这里生成的
是通用的，所以通过人工设计不同的
，可能能引导出不同的
，而
其实就是提示工程里提到的。
表现出来的性质就是强大的上下文学习。

哈夫曼编码唯一吗_平均编码长度怎么求

相关推荐