1. 激活谷首页
  2. 激活谷笔记

fft的计算原理_fft计算量

• 激活谷笔记

fft的计算原理_fft计算量「知乎·致知计划·应用工程·计算方法」《伪谱法实用指南》(Fornberg,1996)——附录F：伪谱法的基于FFT的实现——F.1 FFT算法Fornberg, B. (1996).A practical guide to pseudospectral methods(No. 1). Cambri

「知乎·致知计划·应用工程·计算方法」《伪谱法实用指南》(Fornberg,1996)——附录F：伪谱法的基于FFT的实现——F.1 FFT算法 　　Fornberg, B. (1996).A practical guide to pseudospectral methods(No. 1). Cambridge university press. 　　基础工程 　　目 录 　　附录F：伪谱法的基于FFT的实现 　　周期性伪谱法几乎总是通过使用FFT算法来实现。对于非周期性PS方法，直接的矩阵
\times向量乘法通常既快速又方便。不过，对于Chebyshev伪谱法，余弦FFT方法也很有效。F.1节介绍了FFT概念，F.2和F.3节介绍了FFT在周期性伪谱法和Chebyshev伪谱实现中的应用。 　　在大多数周期性伪谱环境中，实际需要的不是傅里叶展开式系数，而是计算周期性卷积的快速方法。FFT就是这样一种方法。在第F.4节中，我们将讨论卷积和一些有效计算卷积的替代方法。在第F.5节中，我们发现在成本是 “基本”FFT的四倍的情况下，算法的范围可以大大扩展。这些分数阶傅里叶变换适用于许多物理和计算问题。 　　F.1 FFT算法 　　给定
N 个复数
\bbox[#0F0,5px,border:0px solid blue] {u_j, j=0,1, \ldots, N-1} ，正向DFT（离散傅里叶变换）：
\bbox[#0F0,10px,border:10px solid blue] {\hat{u}_k=\frac{1}{N} \sum_{j=0}^{N-1} u_j e^{-2 \pi i k j / N}, \quad k=0,1, \ldots, N-1},\tag{F.1-1}产生同样多的复傅里叶系数
\hat{u}_k。反向DFT：
\bbox[#0F0,10px,border:10px solid blue] {u_j=\sum_{k=0}^{N-1} \hat{u}_k e^{2 \pi i k j / N}, \quad j=0,1, \ldots, N-1},\tag{F.1-2}恢复了初始数
\bbox[#0FF,5px,border:0px solid blue] {u_j, j=0,1, \ldots, N-1} 。 　　将这些方程写成矩阵
\times向量乘积通常非常方便。例如，在(F.1-2)的情况下，我们有：
\bbox[#0FF,10px,border:0px solid blue] {u_j=\sum_{k=0}^{N-1} \hat{u}_k e^{2 \pi i k j / N}, \quad j=0,1, \ldots, N-1,\tag{F.1-2}}
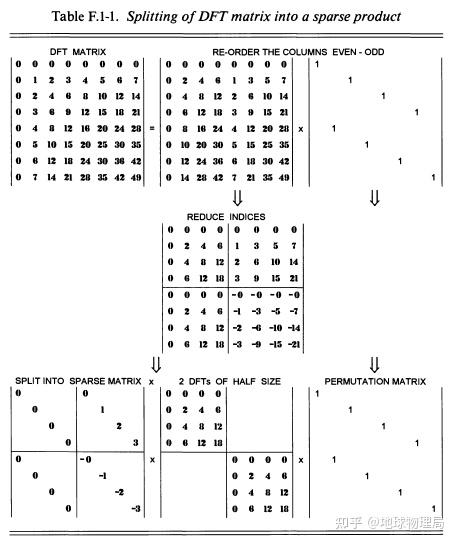
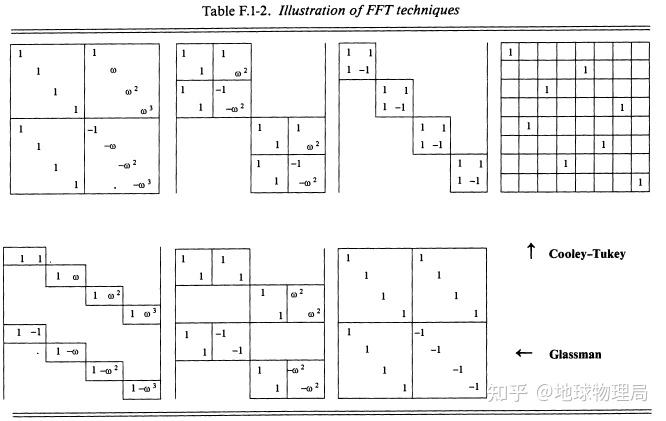
\bbox[#0F0,10px,border:10px solid blue] {\left[\begin{array}{cccccc} 1 & 1 & 1 & 1 & \cdots & 1 \\ 1 & \omega & \omega^2 & \omega^3 & \cdots & \omega^{N-1} \\ 1 & \omega^2 & \omega^4 & \omega^6 & \cdots & \omega^{2 N-2} \\ \vdots & \vdots & & & & \\ \vdots & \vdots & & & & \\ 1 & \omega^{N-1} & \cdots & \cdots & \cdots & \omega^{(N-1)^2} \end{array}\right]\left[\begin{array}{c} \hat{u}_0 \\ \hat{u}_1 \\ \hat{u}_2 \\ \vdots \\ \vdots \\ \hat{u}_{N-1} \end{array}\right]=\left[\begin{array}{c} u_0 \\ u_1 \\ u_2 \\ \vdots \\ \vdots \\ u_{N-1} \end{array}\right]},\tag{F.1-3}其中
\omega=e^{2 \pi i / N} 。 　　快速傅里叶变换(FFT)算法相当于指出，这个DFT矩阵可以写成几个稀疏矩阵的乘积（因此，用几个稀疏矩阵
\times向量乘法取代了(F.1-3)中的全矩阵
\times向量乘法）。当
N 是一个高度复合数，特别是
2 的幂级数时，这种因式分解就变得特别简单和经济。 　　表F.1-1展示了
N=8 情况下的关键因式分解步骤，可以看到DFT矩阵被分解为一个稀疏矩阵、两个一半大小的DFT矩阵和一个置换矩阵的乘积。重复这一过程，立即得到表F.1-2所示的顶层因式分解。FFT因式分解远非唯一。通过将置换纳入稀疏因子，可以得到“自排序”算法（表F.1-2，底部）。下面的FFT代码使用Cooley-Tukey算法，其优点是在矩阵
\times向量乘法过程中不需要额外的数据向量作为中间存储。关于FFT变化的广泛讨论和参考文献，可参见。
fft的计算原理_fft计算量
fft的计算原理_fft计算量表F.1-1 将DFT矩阵拆分为稀疏乘积 　　注：在这个说明中，
N=8 。黑体项
\boldsymbol k 和
-\boldsymbol k 分别是
\omega^k 和
-\omega^k 的简写。关系式
\omega^{k+N}=\omega^k 重复实使用。
fft的计算原理_fft计算量
fft的计算原理_fft计算量表F.1-1 将DFT矩阵分裂为稀疏乘积 　　注：在这个说明中，
N=8 。黑体项
\boldsymbol k 和
-\boldsymbol k 分别是
\omega^k 和
-\omega^k 的简写。关系式
\omega^{k+N}=\omega^k 和
\omega^{k+N / 2}=-\omega^k 重复使用。

2024最新激活全家桶教程，稳定运行到2099年，请移步至置顶文章：https://sigusoft.com/99576.html

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请联系我们举报，一经查实，本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处：https://sigusoft.com/39905.html

赞 (0)
0
上一篇 2024年 9月 7日
下一篇 2024年 9月 7日

相关推荐

关注微信