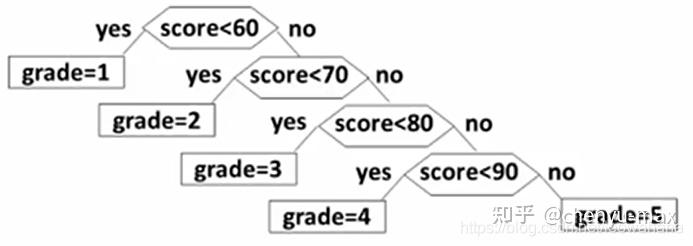
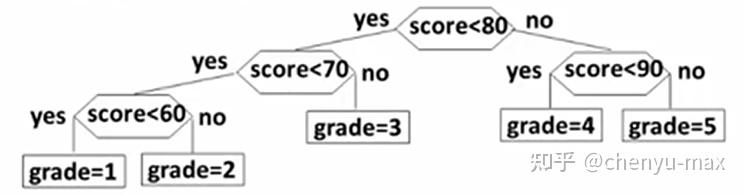
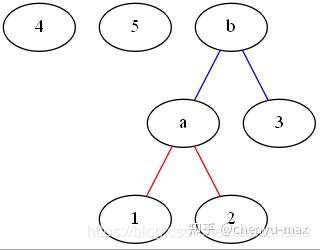
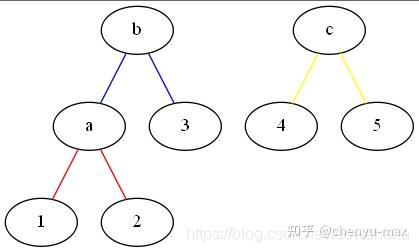
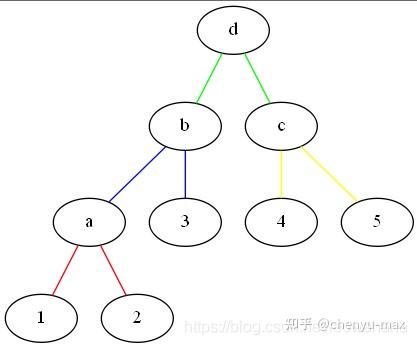
数据结构——哈夫曼树深入浅出含图解（含C++代码实现） 前言 问题：将百分制的成绩变为五分制的成绩 我们将其画为一颗判定树
如果我们学生的成绩绝大多数都是90，80，但是60分的很少，这颗判定树的效率就很低了。 如果考虑学生成绩的分布概率
按照上述的查找方法，查找效率为： 0.05 * 1 + 0.15 * 2 + 0.40 * 3 + 0.30 * 4 + 0.10 * 4 = 3.15 修改判定树
此时的效率就是 0.05 * 3 + 0.15 *3 + 0.4 * 2 + 0.3 * 2 + 0.1 *2 = 2.2 显然比之前的判定树要好 根据这个，给了我们一个启示如何根据结点不同的查找频率构造更有效的搜索树? 这个就是哈夫曼树要解决的问题 哈夫曼树 带权路径长度（WPL）： 设有n个叶子节点，每个叶子节点带有权值$W_k$，从根节点到每个叶节点的长度为$L_k$，则每个叶子节点的带权路径长度之和就是$\sum_{k=0}^nW_k*L_k$ 什么是哈夫曼树 哈夫曼树（Huffman Tree），又称最优二叉树，是一类带权路径长度最短的树。假设有n个权值{w1,w2,…,wn}，如果构造一棵有n个叶子节点的二叉树，而这n个叶子节点的权值是{w1,w2,…,wn}，则所构造出的带权路径长度最小的二叉树就被称为哈夫曼树。 举例 
如图二叉树， WPL = （5+6）* 4 + （2+4）* 3 + 3 * 2 + 1 * 1 = 69 哈夫曼树的特点 哈夫曼树的特点: 没有度为1的结点 ； n个叶子节点数的哈夫曼树，节点总数为2n-1 哈夫曼树的任意非叶节点的左右子树交换后仍是哈夫曼树； 哈夫曼树构建 思路：将权值从小打到进行排序每次把权值最小的两棵二叉树合并，这颗二叉树的权值就是并在一起两棵二叉树权值的和 比如 [1,2,3,4,5]
先将最小的两个子树合并，合并后的权值为两子树权值之和 a = 1 + 2 = 3
再进行排序，将最小两数合并 b = a + 3 = 6
重复12操作 c = 4 + 5 > b
最后再进行合并
此时WPL = (1+2)*3 + 3 * 2 + (4+5) * 2 = 33 代码实现哈夫曼树的构造 这里我运用了我另一篇博客数据结构——堆的基本操作（堆的建立、插入、删除等）详解的知识，这里我运用了最小堆的相关操作，某些函数有所不同，我就不列出了 Ps：本人初学数据结构，若有出现错误，欢迎指出
2024最新激活全家桶教程，稳定运行到2099年，请移步至置顶文章：https://sigusoft.com/99576.html
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请联系我们举报，一经查实，本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处：https://sigusoft.com/35627.html
