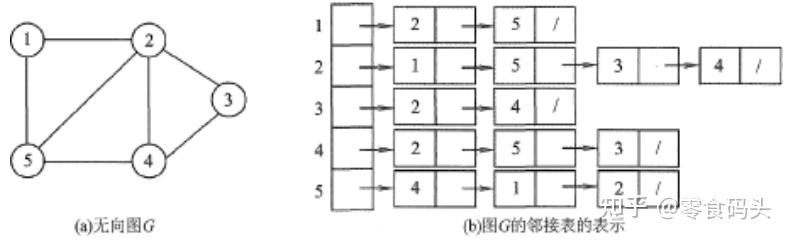
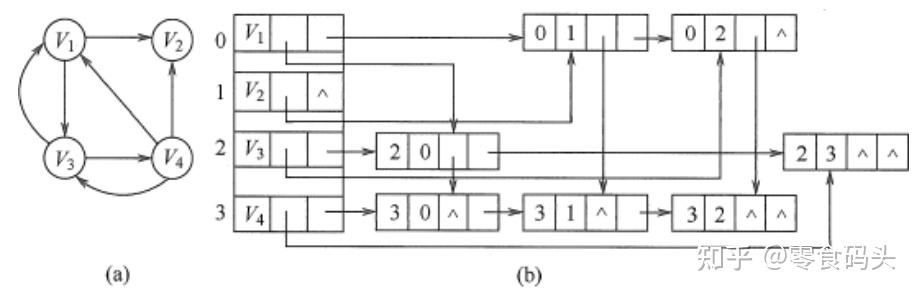
考研保研面试系列(一)—数据结构面试真题整理(打印版) 数据结构面试真题整理 为方便大家背诵,整理的答案都是干货,因为在面试的时候,说了很多但说不到重点上,导师会听烦的,即使答在重点上,也要条理清晰的讲述,切记不要啰啰嗦嗦、磕磕巴巴,保证流畅度和准确度,否则会影响导师对大家的印象。大家直接打印背诵就好了,我主页上还有一篇是背诵版的,背过了之后,可以直接看着背诵版的回忆内容,检查自己的背诵情况~~~ 如果有不对的地方,欢迎大家的批评指正~~~ 里面标注真题的是我被问到过的,或者是身边有朋友同学被问到过的~~~ 1.什么是时间复杂度,空间复杂度,大O表示法? 时间复杂度:一个语句的频度是指该语句在算法中被重复执行的次数。算法中所有语句的频度之和记为T(n),它是该算法问题规模n的函数,时间复杂度主要分析T(n)的数量级。 空间复杂度:算法的空间复杂度S(n)定义为该算法所耗费的存储空间,它是问题规模n的函数。 一般用大O表示法来表示时间复杂度和空间复杂度。以时间复杂度为例子,O(n)这个大O表示的是最坏情况下的时间复杂度,是算法中所有语句的频度之和T(n)的数量级。 2.数据的存储结构有哪几种,每种的优缺点是什么? 存储结构是指数据结构在计算机中的表示,也称物理结构,主要有以下4种: ①顺序存储。 把逻辑上相邻的素存储在物理位置上也相邻的存储单中,素之间的关系由存储单的邻接关系来体现。其优点是可以实现随机存取,每个素占用最少的存储空间;缺点是只能使用相邻的一整块存储单,因此可能产生较多的外部碎片。 ②链式存储。 不要求逻辑上相邻的素在物理位置上也相邻,借助指示素存储地址的指针来表示素之间的逻辑关系。其优点是不会出现碎片现象,能充分利用所有存储单;缺点是每个素因存储指针而占用额外的存储空间,且只能实现顺序存取。 ③索引存储。 在存储素信息的同时,还建立附加的索引表。索引表中的每项称为索引项,索引项的一般形式是(关键字,地址)。其优点是检索速度快;缺点是附加的索引表额外占用存储空间。另外,增加和删除数据时也要修改索引表,因而会花费较多的时间。 ④散列存储。 根据素的关键字直接计算出该素的存储地址,又称哈希(Hash)存储。其优点是检索、增加和删除结点的操作都很快;缺点是若散列函数不好,则可能出现素存储单的冲突,而解决冲突会增加时间和空间开销。 3.介绍一下贪心算法(真题) 就是做出在当前看来是最好的结果,它不从整体上加以考虑,也就是局部最优解。贪心算法从上往下,从顶部一步一步最优,得到最后的结果,它不能保证全局最优解,与贪心策略的选择有关。 4.介绍一下动态规划算法(真题,后面弗洛伊德算法是用的动态规划的思想,提到弗洛伊德的时候很容易会引出动态规划) 是把问题分解成子问题,这些子问题可能有重复,可以记录下前面子问题的结果防止重复计算。动态规划解决子问题,前一个子问题的解对后一个子问题产生一定的影响。在求解子问题的过程中保留哪些有可能得到最优的局部解,丢弃其他局部解,直到解决最后一个问题时也就是初始问题的解。动态规划是从下到上,一步一步找到全局最优解。 5.数组和链表的区别 或 顺序表和链表的区别? 数组:1. 在内存中占据连续的空间2. 占用内存小3. 数组的长度在定义时需要给定,如果存放的数据个数超过了数组的初始大小,会出现溢出4. 数组利用下标定位素,访问速度快,时间复杂度为O(1)5. 插入或删除素可能需要移动大量的数据,时间复杂度为O(n) 链表:1. 在内存中可以占据不连续的空间2. 需要额外存储前驱和后继的信息,总体上需要更多的内存空间3. 链表的长度可以根据实际需要进行伸缩4. 链表访问素相对较慢,需要遍历链表直到找到目标素,时间复杂度O(n)5. 插入或删除素只需修改指针,时间复杂度为O(1) 所以说链表适合多插入删除场景,数组线性表适合多读取场景 6.头指针和头结点的区别? 头指针:是指向第一个节点存储位置的指针,具有标识作用,头指针是链表的必要素,无论链表是否为空,头指针都存在。 头结点:是放在第一个素节点之前,便于在第一个素节点之前进行插入和删除的操作,头结点不是链表的必须素,可有可无,头结点的数据域也可以不存储任何信息。 7.栈和队列的区别? 栈: 先进后出: 是一种后进先出的数据结构,最后进入栈的素最先被访问。栈支持两种基本操作,入栈和出栈。入栈将素添加到栈的顶部,而出栈则移除栈顶的素。栈只允许在栈顶进行操作,即只能访问或修改最后入栈的素。 队列: 先进先出:队列是一种先进先出的数据结构,最先进入队列的素最先被访问。队列支持两种基本操作,即入队和出队。入队将素添加到队列的尾部,而出队则移除队列头部的素。队列允许在队列头部和尾部进行操作,但通常只允许从队列头部出队,从队列尾部入队。 区别: 访问顺序: 栈的访问顺序是后进先出,而队列的访问顺序是先进先出。 栈的主要操作是入栈和出栈,而队列的主要操作是入队和出队。 栈只允许在栈顶进行操作,而队列允许在队列的头尾进行操作,但通常只允许从头部出队、尾部入队。 8.如何区分循环队列是队空还是队满? 由于队空条件和队满条件都是Q.front == Q.rear,为了区分是队空还是队满,三种方式: ①牺牲一个单来区分队空和队满。队满条件是:(Q.rear+ 1) % MaxSize == Q.front ②类型中增设表示素个数的数据成员。队空:Q.size == 0;队满:Q.size == MaxSize ③类型中增设tag数据成员,tag = 0说明是上一步操作是删除,tag = 1说明是上一步操作是插入。队空:Q.front == Q.rear && tag == 0;队满:Q.front == Q.rear && tag == 1。 9.栈和堆的区别?(真题) 先回答什么是栈(详看第7题),再回答什么是堆:堆是一种完全二叉树。分为大顶堆和小顶堆。大顶堆是左右子树的结点值都小于根结点值,左右子树都是大顶堆。小顶堆是左右子树的结点值都大于根结点值,左右子树都是小顶堆。 栈由操作系统自动分配释放,可由操作系统完成静态分配和动态分配,生长方向向下,内存地址由高到低,分配专门的寄存器存放栈的地址,压栈出栈都有专门的指令执行,效率较高; 堆由开发人员分配和释放,只能动态分配,生长方向向上,内存地址由低到高,由库函数或运算符来完成申请与管理,效率较低。 10.什么是串的模式匹配?简介一下KMP算法? 子串的定位操作通常称为串的模式匹配,他求的是子串(常称模式串)在主串中的位置。 在说KMP算法的时候,先来谈一谈暴力模式匹配算法,它的思想是从主串的第一个字符起,与子串的第一个字符比较,相等则继续比较; 不等则从主串的下一个位置起,继续和子串开始比较,直到最后看是否匹配成功。 而KMP算法呢,就是对暴力模式匹配算法的一个改进版本,在暴力匹配中,每趟匹配失败都是模式后移一位再从头开始比较。这样其实无形中增加了匹配的次数。所以可以从分析模式本身的结构着手,如果已匹配相等的前缀序列中有某个后缀正好是模式的前缀,那么就可以将模式向后滑动到与这些相等字符对齐的位置,主串i指针无须回溯, 并继续从该位置开始进行比较。而模式向后滑动位数的计算仅与模式本身的结构有关,与主串无关。这样其实是保证了主串的指针是一直向前走的,不会后退,也使得它的效率大大提高。 (在面试的时候可以适当加一些口语化内容,如果全是很书面专业的,老师会觉得:这小子,背的挺熟啊!所以说适当用口语化的内容可以拉近你和老师之间的距离,让老师觉得你没有在背,而是我本身脑子里就有东西,现在只不过是把它们讲出来,老师会随着你的引导,听你娓娓道来的讲述,老师能听进去你的答案,你就赢了) 11.树的概念性知识,什么是树?什么是二叉树?什么是满二叉树?什么是完全二叉树? 树:树是非线性结构,其素之间有明显的层次关系。在树的结构中,每个节点都只有一个前件称为父节点,没有前件的节点为树的根节点,简称为树的根;每个节点可以有多个后件成为节点的子节点,没有后件的节点称为叶子节点。 二叉树:二叉树是另一种树形结构,其特点是每个结点至多只有两棵子树,并且二叉树的子树有左右之分,其次序不能任意颠倒。二叉树可以用递归的形式定义。 满二叉树:满二叉树是指除了最后一层外其他节点均有两颗子树。 完全二叉树:完全二叉树是指除了最后一层外,其他任何一层的节点数均达到最大值,且最后一层也只是在最右侧缺少节点。 12.树的存储结构? 树有三种存储结构,分别是: ①双亲表示法 这种存储方式采用一组连续空间来存储每个结点,同时在每个结点中增设一个伪指针,指示其双亲结点在数组中的位置。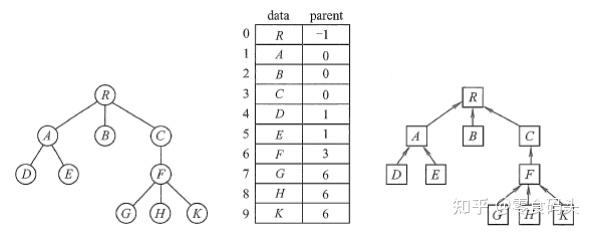
2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/20835.html






