一.数列极限的定义
数列
如果按照某一法则,对每个 n ∈ N n \in N n∈N,对应着一个确定的实数 x n x_n xn,这些实数 x n x_n xn按照下标 n n n从小到大排列得到的一个序列
x 1 , x 2 , x 4 , ⋅ ⋅ ⋅ , x n , ⋅ ⋅ ⋅ x_1,x_2,x_4,···,x_n,··· x1,x2,x4,⋅⋅⋅,xn,⋅⋅⋅
就叫做数列,简记为数列 { x n } \{x_n\} {
xn}.
数列中的每一个数叫做数列的项,第 n n n项 x n x_n xn叫做数列的一般项(或通项)
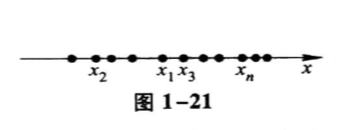
在几何上,数列 { x n } \{x_n\} {
xn}可看作数轴上的一个动点,它依次取数轴上的点 x 1 , x 2 , x 4 , ⋅ ⋅ ⋅ , x n , ⋅ ⋅ ⋅ x_1,x_2,x_4,···,x_n,··· x1,x2,x4,⋅⋅⋅,xn,⋅⋅⋅(如下图)
等差数列 { x n } {\{x_n\}} {
xn}:公差 d = x n − x n − 1 ∈ R d=x_n-x_{n-1}∈R d=xn−xn−1∈R,通项公式为 x n = x 1 + ( n − 1 ) d x_n=x_1+(n-1)d xn=x1+(n−1)d,前n项求和公式为 S n = n ( x 1 + x n ) 2 S_{n}\mathrm{=}\frac{n\left(x_{1}\mathrm{+}x_{n}\right)}{2} Sn=2n(x1+xn)
等比数列 { x n } {\{x_n\}} {
xn}:公比 q = x n x n − 1 q=\frac{x_{n}}{x_{n-1}} q=xn−1xn,通项公式为 x n = x 1 ∗ q n − 1 x_n=x_1*q^{n-1} xn=x1∗qn−1,前n项求和公式为 S n = x 1 ( 1 − q n ) 1 − q S_{n}\mathrm{=}\frac{x_1\left(1\mathrm{-}q^{n}\right)}{1-q} Sn=1−qx1(1−qn)
数列 { x n } \{x_n\} {
xn}可看作自变量为正整数 n n n的函数
x n = f ( n ) , n ∈ N + x_n = f(n), n \in N_+ xn=f(n),n∈N+
当自变量 n n n依次取1,2,3,···一切正整数时,对应的函数值就排列成数列 { x n } \{x_n\} {
xn}
数列的极限
如果当数列 { x n } \{x_n\} {
xn}的项数n无限增大时,它的一般项 x n x_n xn无限接近于一个确定的常数a,则称a为数列 { x n } \{x_n\} {
xn}的极限.此时也称数列 { x n } \{x_n\} {
xn}收敛于a,记作 lim n → ∞ x n = a \operatorname*{lim}_{n\to\infty}x_{n}=a limn→∞xn=a,或 x n → a ( n → ∞ ) x_n→a(n→∞) xn→a(n→∞).例如, lim n → ∞ n + ( − 1 ) n + 1 n = 1 \lim\limits_{n\to\infty}\dfrac{n+\left(\begin{array}{c}-1\end{array}\right)^{n+1}}{n}=1 n→∞limnn+(−1)n+1=1。
如果当数列 { x n } \{x_n\} {
xn}的项数n无限增大时,它的一般项 x n x_n xn不接近于任何确定的常数,则称数列 { x n } \{x_n\} {
xn}没有极限,或称数列 { x n } \{x_n\} {
xn}发散,习惯上记作 lim n → ∞ x n \operatorname*{lim}_{n\to\infty}x_{n} limn→∞xn不存在.例如, lim n → ∞ ( − 1 ) n − 1 \operatorname*{lim}_{n\to\infty}\left(-1\right)^{n-1} limn→∞(−1)n−1不存在.
当数列 { x n } \{x_n\} {
xn}的项数n无限增大时,如果 | x n | |x_n| |xn|也无限增大,则数列 { x n } \{x_n\} {
xn}没有极限.此时,习惯上也称数列 { x n } \{x_n\} {
xn}的极限是无穷大,记作 lim n → ∞ x n = ∞ \operatorname*{lim}_{n\to\infty}x_{n}=\infty limn→∞xn=∞.例如 lim n → ∞ 3 n − 1 = ∞ \lim\limits_{n\to\infty}3^{n-1}=\infty\quad n→∞lim3n−1=∞.
数列极限的定义
一般地,有如下数列极限的定义:
定义 设 { x n } \{x_n\} {
xn}为一数列,如果存在常数 a a a,对于任意给定的正数 ε \varepsilon ε(不论它多么小),总存在正整数 N N N,使得当 n > N n > N n>N时,不等式
∣ x n − a ∣ < ε |x_n – a| < \varepsilon ∣xn−a∣<ε
都成立,那么就称常数 a a a是数列 { x n } \{x_n\} {
xn}的极限,或者称数列 { x n } \{x_n\} {
xn}收敛于 a a a,记为
lim n → ∞ x n = a \lim\limits_{n \to \infty}x_n = a n→∞limxn=a
或
x n → a ( n → ∞ ) x_n \rightarrow a(n \rightarrow \infty) xn→a(n→∞)
如果不存在这样的常数 a a a,就说数列 { x n } \{x_n\} {
xn}没有极限,或者说数列 { x n } \{x_n\} {
xn}是发散的,习惯上也说 lim n → ∞ x n \lim\limits_{n \to \infty}x_n n→∞limxn不存在
数列极限 lim n → ∞ x n = a \lim\limits_{n \to \infty}x_n = a n→∞limxn=a的定义可表达为
lim n → ∞ x n = a ⇔ ∀ ε > 0 , ∃ 正整数 N , 当 n > N 时 , 有 ∣ x n − a ∣ < ε \lim\limits_{n \to \infty}x_n = a \Leftrightarrow \forall \varepsilon > 0,\exists 正整数 N,当 n > N时,有|x_n – a| < \varepsilon n→∞limxn=a⇔∀ε>0,∃正整数N,当n>N时,有∣xn−a∣<ε
注
(1)定义中, ε ε ε刻画了 x n x_n xn和 a a a的接近程度, ε ε ε的“任意”性极其重要.只有这样, ∣ x n − a ∣ < ε |x_n-a|<ε ∣xn−a∣<ε才能体现 x n x_n xn和 a a a的“无限接近”;
(2)正整数 N N N与任意给定的正数 ε ε ε有关.对于给定的 ε ε ε,相应的 N N N不是唯一的,即只要其存在,并没有要求其达到最小;
(3)由定义也可看出, { x n } \{x_n\} {
xn}的极限是否存在仅与它的发展趋势有关.只要从某项 N N N开始, ∣ x n − a ∣ < ε |x_n-a|<ε ∣xn−a∣<ε即可,与前有限项的变化无关.
二.数列极限的计算
极限的定义只能用来验证极限,而不能计算数列的极限,所以下面给出数列极限的运算法则.
定理(数列极限的运算法则) 若 lim n → ∞ x n = a , lim n → ∞ y n = b \lim\limits_{n\to\infty}x_{n}=a,\lim\limits_{n\to\infty}y_{n}=b n→∞limxn=a,n→∞limyn=b,则
- lim n → ∞ ( x n ± y n ) = lim n → ∞ x n ± lim n → ∞ y n = a ± b (加减法则) \lim\limits_{n\to\infty}(x_n\pm y_n)=\lim\limits_{n\to\infty}x_n\pm\lim\limits_{n\to\infty}y_n=a\pm b(加减法则) n→∞lim(xn±yn)=n→∞limxn±n→∞limyn=a±b(加减法则)
- lim n → ∞ ( x n ∗ y n ) = lim n → ∞ x n ∗ lim n → ∞ y n = a ∗ b (乘法法则) \lim\limits_{n\to\infty}(x_n*y_n)=\lim\limits_{n\to\infty}x_n*\lim\limits_{n\to\infty}y_n=a*b(乘法法则) n→∞lim(xn∗yn)=n→∞limxn∗n→∞limyn=a∗b(乘法法则)
- lim n → ∞ x n = lim n → ∞ x n = a ( x n ⩾ 0 , a ⩾ 0 ) (交换法则) \lim\limits_{n\to\infty}\sqrt{x_n}=\sqrt{\lim\limits_{n\to\infty}x_n}=\sqrt{a}(x_n\geqslant0,a\geqslant0)(交换法则) n→∞limxn=n→∞limxn=a(xn⩾0,a⩾0)(交换法则)
- lim n → x x n y n = lim n → x x n lim n → x y n = a b ( lim n → x y n = b ≠ 0 ) (除法法则) \lim\limits_{n\to\boldsymbol{x}}\dfrac{x_n}{y_n}=\dfrac{\lim_{n\to\boldsymbol{x}}x_n}{\lim_{n\to\boldsymbol{x}}y_n}=\dfrac{a}{b}(\lim_{n\to\boldsymbol{x}}y_n=b\neq0)(除法法则) n→xlimynxn=limn→xynlimn→xxn=ba(n→xlimyn=b=0)(除法法则)
三.收敛数列的性质
定理1(极限的唯一性) \; 如果数列 { x n } \{x_n\} {
xn}收敛,那么它的极限唯一
定理2(收敛数列的有界性) \; 如果数列 { x n } \{x_n\} {
xn}收敛,那么数列 { x n } \{x_n\} {
xn}一定有界
定理3(收敛数列的保号性) \; 如果 lim n → ∞ x n = a \lim\limits_{n \to \infty}x_n = a n→∞limxn=a,且 a > 0 a > 0 a>0(或 a < 0 a < 0 a<0),那么存在正整数 N N N,当 n > N n > N n>N时,都有 x n > 0 x_n > 0 xn>0(或 x n < 0 x_n < 0 xn<0)
推论 \; 如果数列 { x n } \{x_n\} {
xn}从某项起有 x ≥ 0 x \geq 0 x≥0 (或 x ≤ 0 x \leq 0 x≤0),且 lim n → ∞ x n = a \lim\limits_{n \to \infty}x_n = a n→∞limxn=a,那么 a ≥ 0 a \geq 0 a≥0(或 a ≤ 0 a \leq 0 a≤0)
定理4(收敛数列与其子数列间的关系) \; 如果数列 { x n } \{x_n\} {
xn}收敛于 a a a,那么它的任一子数列也收敛,且极限也是 a a a
2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/169151.html