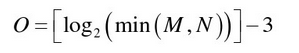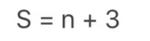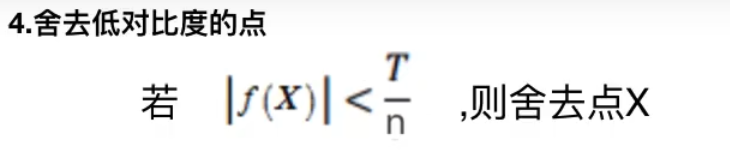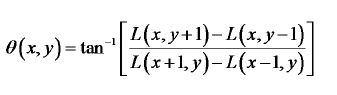sift特征点提取步骤_sift特征128维

sift（尺度不变特征变换）

参考

一、sift 算法的目标

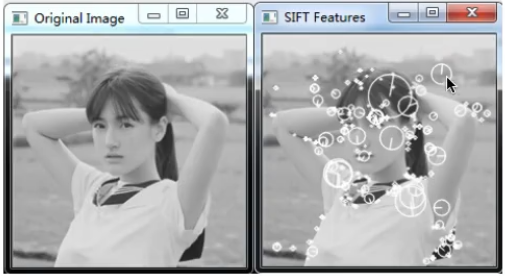
sift 的目标是： 找到一幅图像中的一些稳定的保持不变性的局部特征点，该特征点被一个特殊向量描述。该特征点的特征叫做sift特征

1999年British Co1umbia大学大卫.劳伊（ David G.Lowe）教授总结了现有的基于不变量技术的特征检测方法，并正式提出了一种基于尺度空间的、对图像缩放、旋转甚至仿射变换保持不变性的图像局部特征描述算子-SIFT(尺度不变特征变换），这种算法在2004年被加以完善。

1.哪些点是SIFT中要查找的关键点（特征点)?
这些点是一些十分突出的点不会因光照条件的改变而消失，比如角点、边缘点、暗区域的亮点以及亮区域的暗点，既然两幅图像中有相同的景物，那么使用某种方法分别提取各自的稳定点，这些点之间会有相互对应的匹配点。
所谓关键点，就是在不同尺度空间的图像下检测出的具有方向信息的局部极值点。
根据归纳,我们可以看出特征点具有的三个特征:
尺度 方向 大小

二、sift特征的特点

1. 对旋转、尺度缩放、亮度变化保持不变性，对视角变化、噪声等也存在一定程度的稳定性；
2. 独特性，信息量丰富，适用于在海量特征数据中进行快速，准确的匹配；
3. 多量性，即使少数几个物体也可以产生大量的Sfit特征向量；
4. 可扩展性，可以很方便的与其他形式的特征向量进行联合；

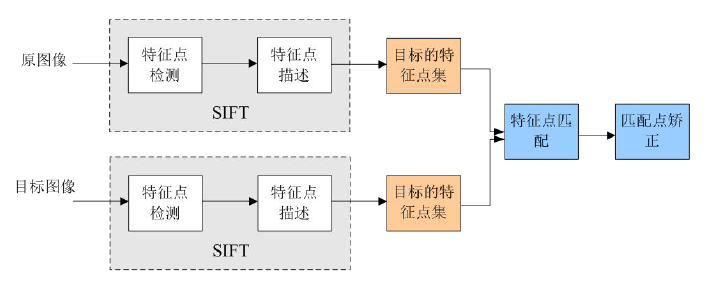
三、sift特征的匹配

Sfit算法的实质是在不同的尺度空间上查找关键点（特征点），计算关键点的大小、方向、尺度信息，利
用这些信息组成关键点对特征点进行描述的问题。Sift所查找的关键点都是一些十分突出，不会因光照，
仿射变换和噪声等因素而变换的“稳定”特征点，如角点、边缘点、暗区的亮点以及亮区的暗点等。
匹配的过程就是对比这些特征点的过程：

四、sift特征提取和匹配具体步骤

1. 生成高斯金字塔
2. 生成高斯差分金字塔（DOG金字塔），尺度空间构建
3. 空间极值点检测（关键点的初步查探）
4. 稳定关键点的精确定位
5. 稳定关键点方向信息分配
6. 关键点描述
7. 特征点匹配

1. 生成高斯金字塔

2.什么是尺度空间( scale space ) ?
我们要精确表示的物体都是通过一定的尺度来反映的。现实世界的物体也总是通过不同尺度的观察而得到不同的变化。
尺度空间理论最早在1962年提出，其主要思想是通过对原始图像进行尺度变换，获得图像多尺度下的尺度空间表示序列，对这些序列进行尺度空间主轮廓的提取，并以该主轮廓作为-种特征向量，实现边缘、角点检测和不同分辨率.上的特征提取等。尺度空间中各尺度图像的模糊程度逐渐变大，能够模拟人在距离目标由近到远时目标在视网膜.上的形成过程。尺度越大图像越模糊。（同一个物体近大远小，近清楚远模糊）尺度空间就是图片的大小
3.为什么选择高斯核来生成尺度空间 ?
根据文献《Scale-space theory: A basic tool for analys ingstructures at different scales》 我们可知，高斯核是唯一可以产生多尺度空间的核，一个图像的尺度空间L (x,y, σ) ,定义为原始图像I(x,y)与一个可变尺度的2维高斯函数G(x,y, σ)卷积运算。

其中xi,yi是中心点坐标，σx=σy=σ是方差
高斯模糊的性质
●
高斯模糊具有圆对称性。
高斯模糊具有线性可分的性质，也可以在二维图像.上对两个独立的一维空间分别进行计算。这样可以大大减少了运算的次数。对一幅图像进行多次连续高斯模糊的效果与一次更大的高斯模糊可以产生同样的效果，大的高斯模糊的半径是所用多个高斯模糊半径平方和的平方根。例如，使用半径分别为6和8的两次高斯模糊变换得到的效果等同于一次半径为10的高斯模糊效果,6²+8²=10²
根据这个关系，使用多个连续较小的高斯模糊处理不会比单个高斯较大处理时间要少。

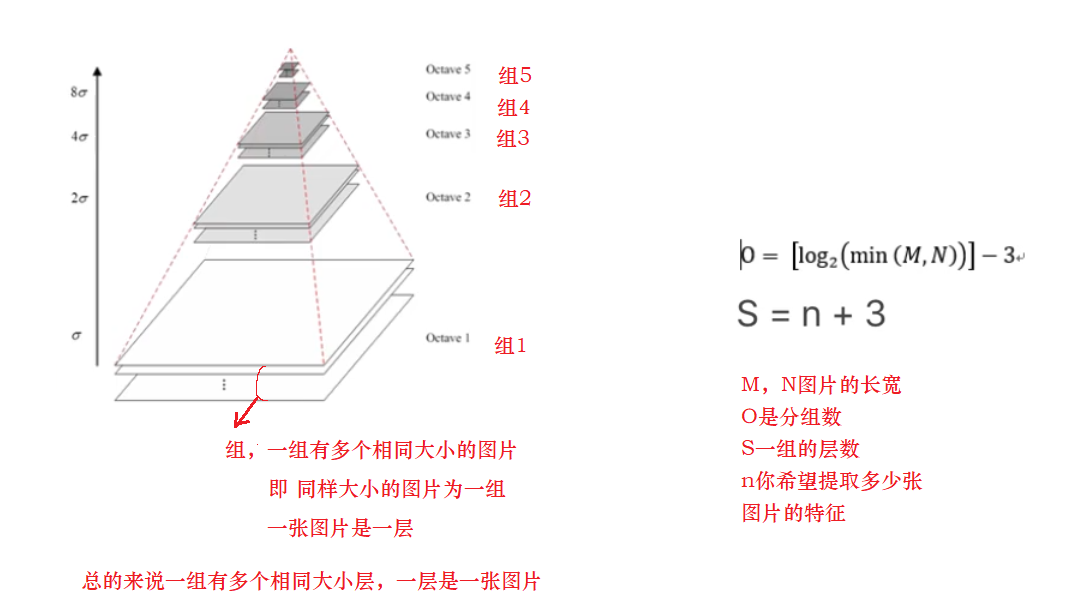
图像高斯金字塔(Gaussian Pyramid)是采用高斯函数对图像进行模糊以及降采样处理得到。其形成过程可如下图所示：

图像金字塔是由大小不用的图像组构成。每组中的图片称为层，每一层图片都是由高斯卷积得到，不同层使用的高斯核的方差（σ值）不同。
高斯金字塔构建过程：

1. 先将原图像扩大一倍之后作为高斯金字塔的第1组第1层，将第1组第1层图像经高斯卷积（其实就
   是高斯平滑或称高斯滤波）之后作为第1组金字塔的第2层。
2. 将σ乘以一个比例系数k，得到一个新的平滑因子σ=k*σ，用它来平滑第1组第2层图像，结果图像作
   为第3层。
3. 如此这般重复，最后得到L层图像，在同一组中，每一层图像的尺寸都是一样的，只是平滑系数不
   一样。它们对应的平滑系数分别为：0，σ，kσ，k^2σ,k3σ……k^(L-2)σ。
4. 将第1组倒数第三层图像作比例因子为2的降采样（尺寸减半），得到的图像作为第2组的第1层，
   然后对第2组的第1层图像做平滑因子为σ的高斯平滑，得到第2组的第2层，就像步骤2中一样，如
   此得到第2组的L层图像，同组内它们的尺寸是一样的，对应的平滑系数分别为：0，σ，kσ，
   k^2σ,k3σ……k^(L-2)σ。但是在尺寸方面第2组是第1组图像的一半。

反复执行，就可以得到一共O组，每组L层，共计O*L个图像，这些图像一起就构成了高斯金字塔

金字塔的分组数O是由输入图像的大小来确定的。公式如下：
高斯金字塔的组数：

其中：M、N分别为图像的行数和列数，O为金字塔的分组数
每一组的分层数S：

其中 S是每一组的分层数，n为对每个组提取特征的层数。
第一组的第一层的高斯半径如何确定。假定世界中的景物是绝对清晰的，照相机对其拍照取得的图像相当于对自然界的景物进行了一次高斯模糊，根据经验，可以假定这次高斯模糊的σ0 = 0.5，而我们想让第一组的第一层图像的为高斯模糊处于σ = 1.6 一次需要在σ0 = 0.5的基础上在进行σ = 1.52的高斯模糊，因此一组的第一层的高斯半径σ = 1.52

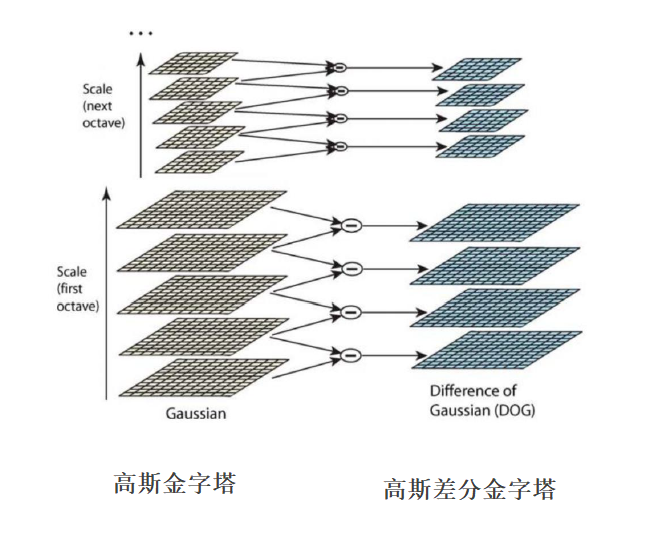
2. 生成高斯差分金字塔

使用高斯金字塔每组中相邻上下两层图像相减，就得到下图的高斯差分金字塔，相减后会出现负数，要做归一化。

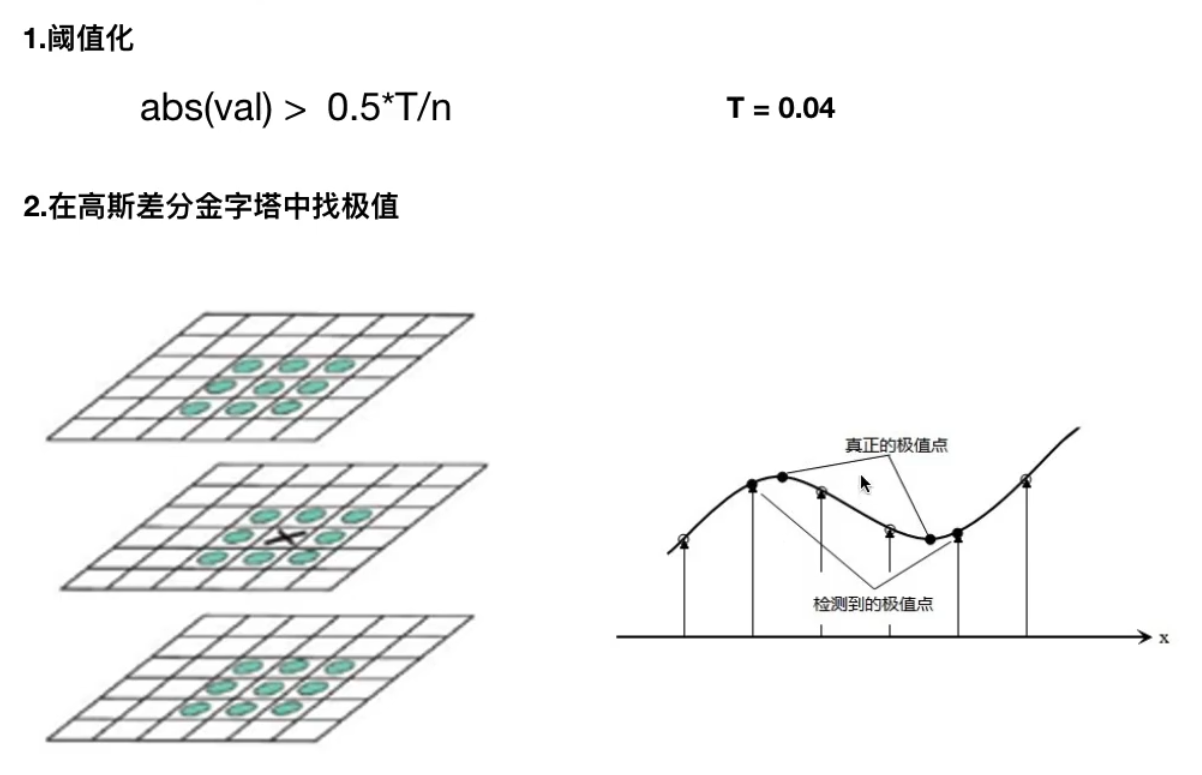
3. 空间极值点检测（关键点的初步查探）

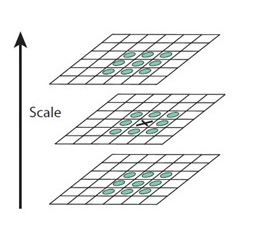
特征点是由DOG空间的局部极值点组成的。为了寻找DoG的极值点，每一个像素点要和它所有的相邻
点比较，看其是否比它的图像域和尺度域的相邻点大或者小。
如下图，中间的检测点和它同尺度的8个相邻点和上下相邻尺度对应的9×2个点共26个点比较，以确保
在尺度空间和二维图像空间都检测到极值点。

注意，局部极值点都是在同一个组当中进行的，所以肯定有这样的问题，某一组当中的第一个图和
最后一个图层没有前一张图和下一张图，那该怎么计算？ 解决办法是，再用高斯模糊，在高斯金字
塔多“模糊”出三张来凑数，所以在DOG中多出两张。（同一组中第一层和最后一层不做极值点检测）

4. 稳定关键点的精确定位

1 简单处理：

DOG值对噪声和边缘比较敏感，所以在第3步的尺度空间中检测到的局部极值点还要经过进一步的筛
选，去除不稳定和错误检测出的极值点。（把较小或者较大的极值点去掉）
利用阈值的方法来限制，在opencv中为contrastThreshold。

2 复杂处理：

求泰勒展开式的极值

此时得到了精确的极值点坐标了（坐标是相对于原图的，如果是在缩小图上（金字塔上层）的到的坐标，则改坐标需要放大到和原图一致）

海森矩阵H(x,y) 可以描述曲率。如果图像的某一点在x，y方向曲率相差太大 则该处很大程度上是边缘。根据数学结论，海森矩阵的特征值是根曲率成正比的，因此我们可以用海森矩阵的特征值来近似代替曲率，又因为特征值很难算，我们用海森矩阵的迹和行列式值来代替海森矩阵的特征值。设其一个特征值为α，一个为β，且α>β,α=γβ，则，海森矩阵的迹为α+β，行列式为αβ，行列式小于0则αβ<0,曲率异号，是边缘，应去除。同号的话，用迹的平方比上行列式的值，该值在γ>1上单调递增，又因为我们希望两个方向的曲率相近这样才不会有边缘效应，因此我们该值应小于γ=10时的值，若结果不满足该条件则也舍去

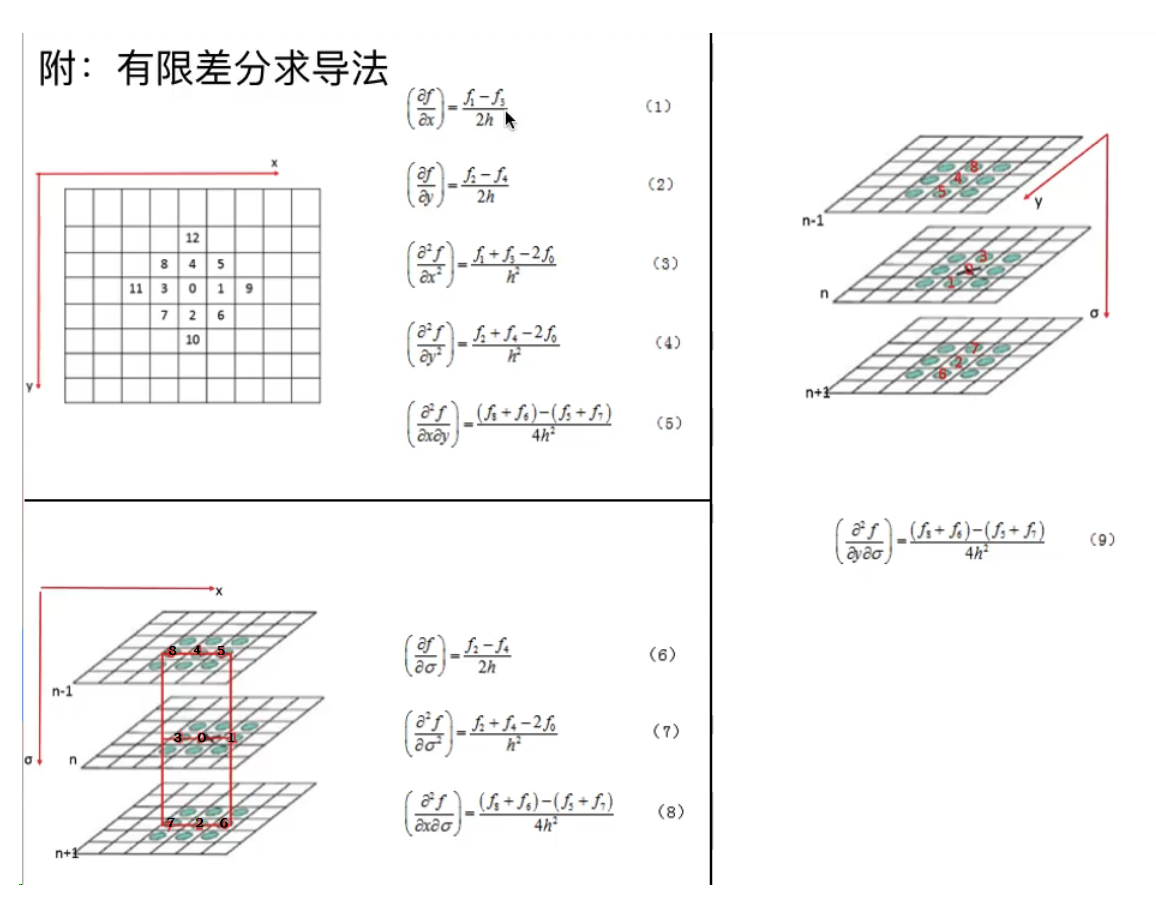
3 求导方法

5. 为稳定关键点赋予方向信息

稳定的极值点是在不同尺度空间下提取的，这保证了关键点的尺度不变性。
为关键点赋予方向信息所要解决的问题是使得关键点对图像角度和旋转具有不变性。
假设特征点坐标为（x0,y0,σ0），找到与σ0最接近的高斯模糊图像（高斯金字塔中的高斯模糊图像而非高斯查分金字塔），假设是尺度为σ的高斯模糊图像。
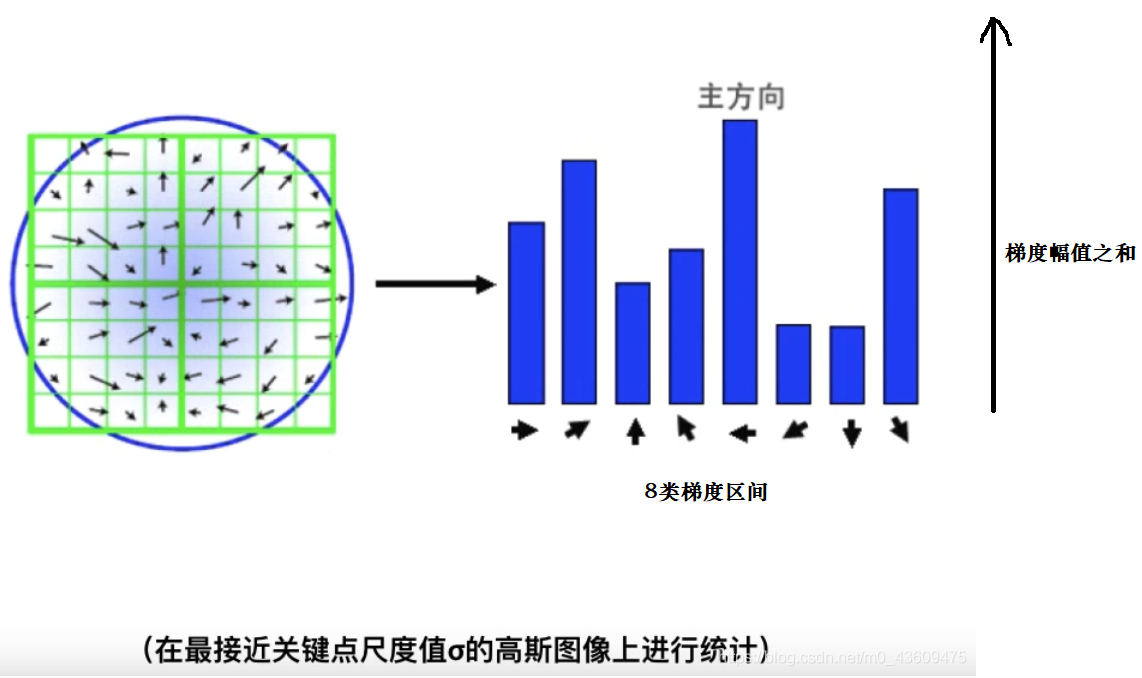
统计以特征点（x0,y0,σ0）为圆心，在该特征点所在的高斯模糊图像的尺度的1.5倍为半径的圆内（即半径为1.5σ），计算所有的像素的梯度方向及其梯度幅值，并做1.5σ的高斯加权，即距离特征点越近的梯度越重要。接着对高斯加权后的梯度结果创建梯度直方图。梯度直方图方法如下：
将梯度方向分类，可分为4类，8类，36类等的都可以，如果分类8类则将角度分为0°-45°，45°-90°，…，315°-360°等8个区间,每45°算一个区间，实际在使用的时候是分36类，每10°算一个区间。统计落到每个区间中的梯度幅值之和，从而生成梯度直方图。直方图的峰值为特征点主方向的参数（对应梯度方向区间），其他高于主方向百分之80的方向被判定为特征点辅助方向。

对于任一关键点（x，y），其梯度幅值表述为：（确定了特征点在确定的高斯模糊图像上时 尺度信息就没有了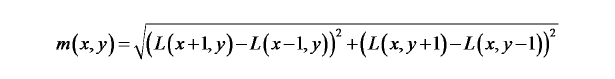）梯度方向为：

6. 构建关键点描述符

对于每一个关键点，都拥有位置、尺度以及方向三个信息。所以具备平移、缩放、和旋转不变性。
为了将两张图片的关键点相互匹配起来，我们就要对关键点构建出一种描述符号，来表示该关键点。
对每个关键点建立一个描述符，用一组向量将这个关键点描述出来（在sift中是一个128维的向量），使其不随各种变化而改变，比如光照变化、视角变化等等描述子不但包含关键点，也包括关键点周围对其有贡献的邻域点。描述的思路是：对关键点周围像素区域分块，计算块内梯度直方图，生成具有独特性的向量，这个向量是该区域图像信息的一种抽象表述。

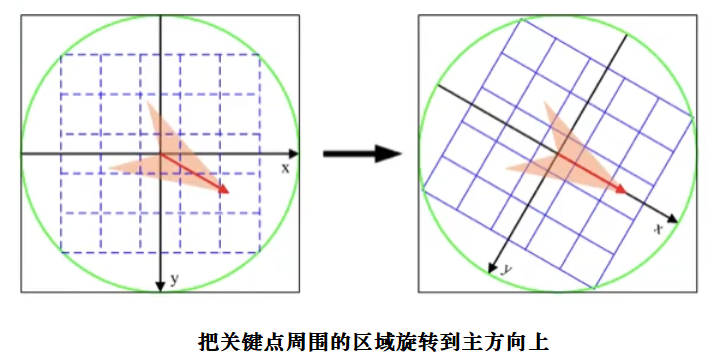
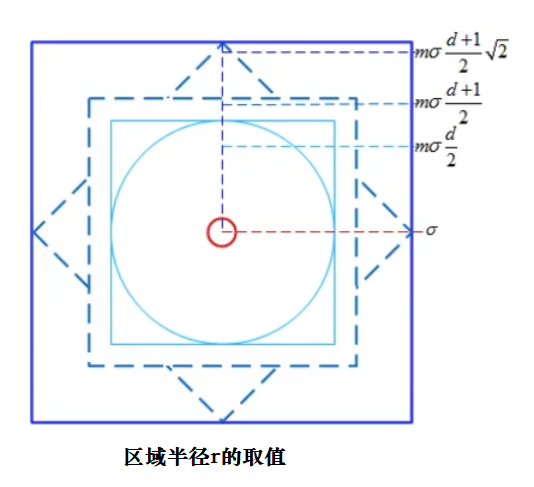
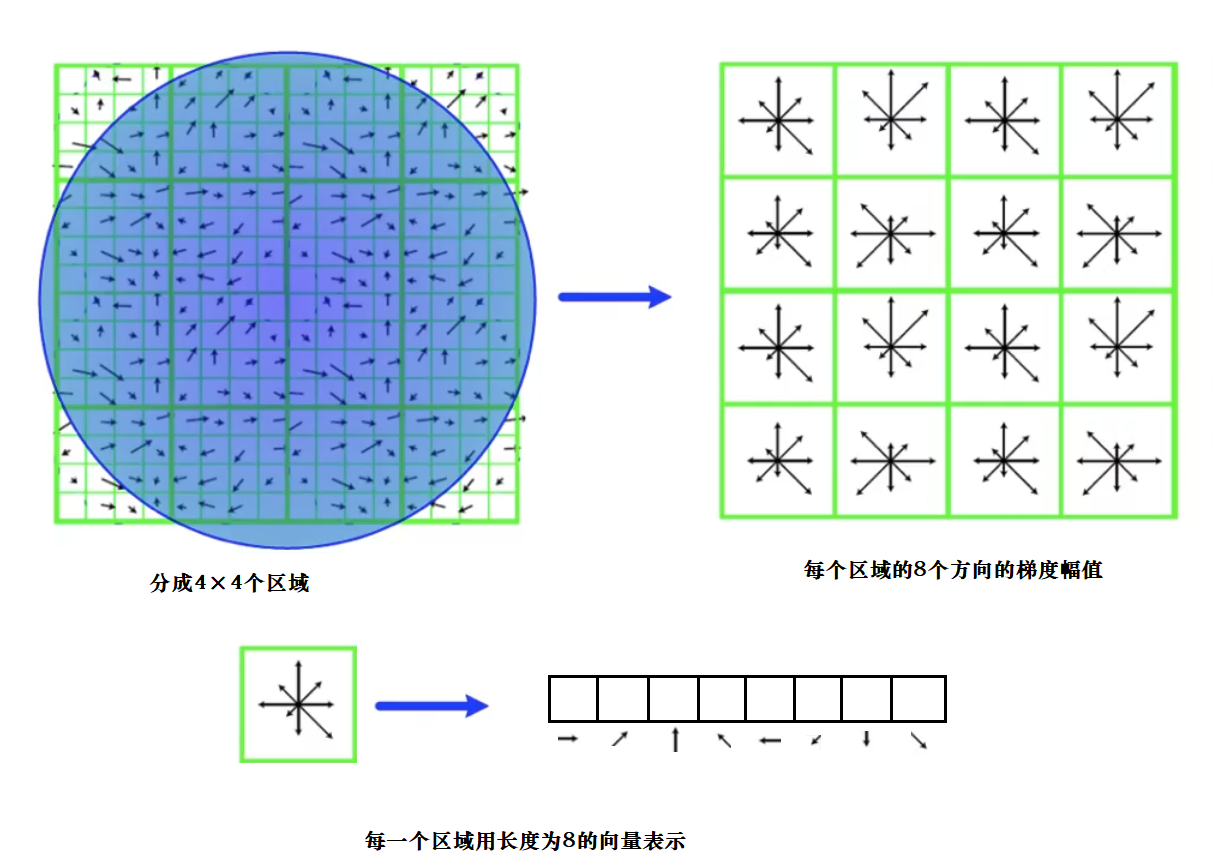
对每个关键点，让该关键点周围区域旋转到主方向上，然后我们取以关键点为圆心半径为r的圆的外接正方形区域，将其分成4×4个子区域，其中子区域以像素为单位。在每个子区域内进行统计每个像素点在8个方向上的梯度幅值（梯度长度），（8个方向为东，西，南，北，东南，东北，西南，西北）梯度幅值是经过高斯加权的（也可以不加权）。每个区域用长度为8的向量表示，16个这样的子区域的向量写在一起构成的长度128一维的向量就是该关键点的描述符。

对于区域半径的选择如下图。其中m取3，σ是关键点的尺度坐标，mσ为每个子区域的宽度。d是子区域的个数。

7. 特征点匹配

对于使用sift关键点做两幅图的对应，我们只需要使用关键点描述符，即计算两幅图像的关键点描述符的相似度，如果相似度在给定范围内则，该点是对应的。
相似度计算可以使用欧式距离或者knn。