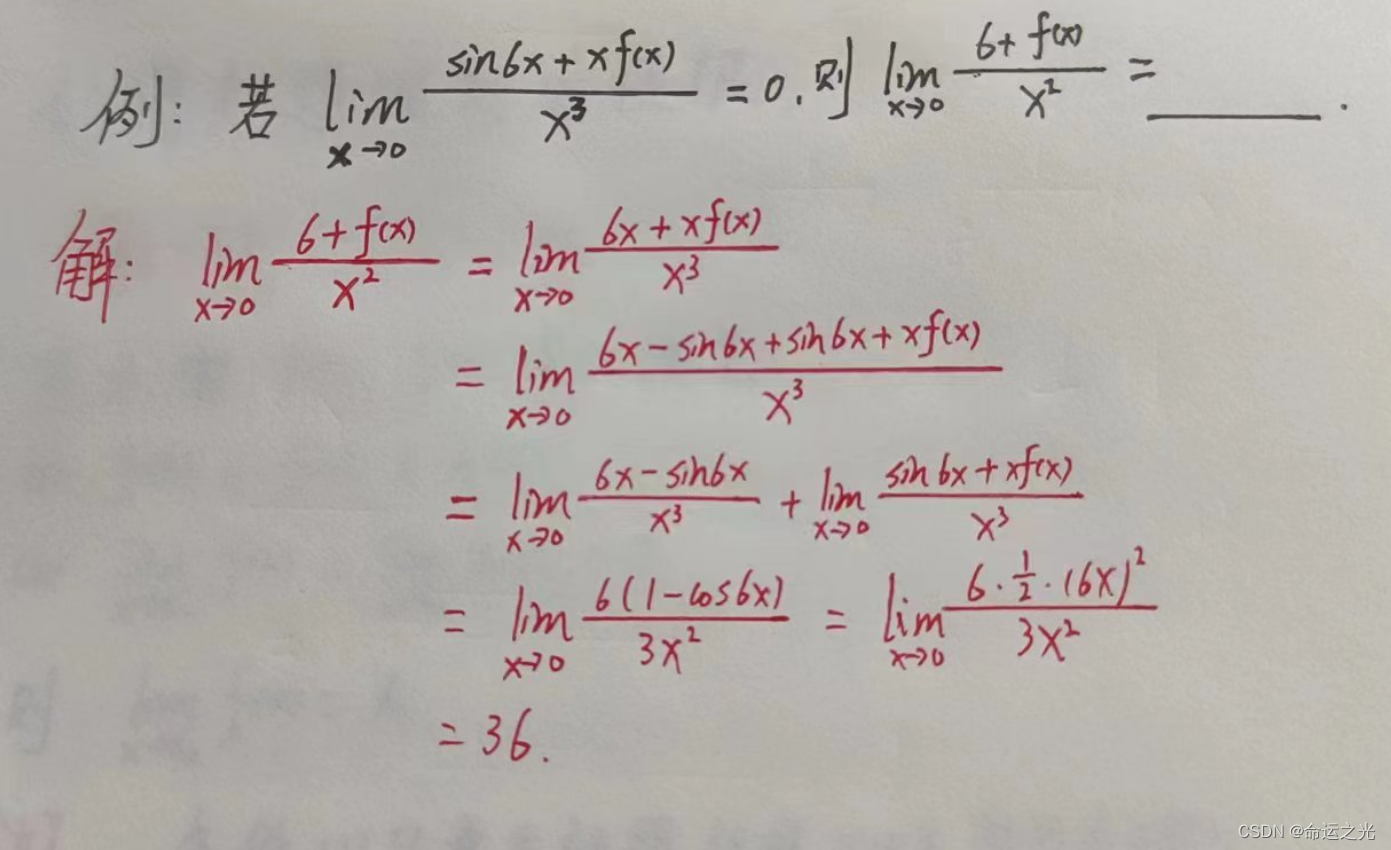高数第一章函数与极限总结_高中数学洛必达法则

2024年 7月 5日下午3:18 • 激活谷笔记

【精讲】高等数学中的洛必达法则

博主：命运之光的主页

专栏：高等数学

【精讲】高等数学中的洛必达法则

导言

一、洛必达法则的定义

二、洛必达法则的条件：为了使用洛必达法则，以下条件必须满足：

三、洛必达法则的证明

必需记忆知识点

知识点1

知识点2

编辑

例题（用于熟悉高等数学中的洛必达法则）

例题1

例题2

例题3

例题4

例题5

例题6

例题7

例题8

例题9

例题10

例题11

例题12

例题13

例题14

结论

导言

在高等数学学习中，我们经常遇到一些复杂的极限计算问题，特别是当极限的形式为0/0或∞/∞时，常规的极限运算法则无法直接得出结果。此时，洛必达法则作为一种强大的工具，为我们解决不定式极限问题提供了简单而高效的方法。本文将详细讲解洛必达法则的定义、条件、证明过程，并通过多个实例展示其在高等数学中的应用。

一、洛必达法则的定义

洛必达法则是用来解决0/0型或∞/∞型的不定式极限问题的重要方法。它的核心思想是通过对函数的分子和分母同时求导，得到一个新的极限形式，进而简化原始的极限计算。

二、洛必达法则的条件：为了使用洛必达法则，以下条件必须满足：

极限形式为0/0或∞/∞，即分子和分母分别趋向于零或无穷大。
分子和分母的极限都存在，并且分母的导数不为零。

三、洛必达法则的证明

洛必达法则的证明基于泰勒展开和导数的定义。在此处，我们将略过具体的证明过程，仅简要介绍其思路。首先，我们利用泰勒展开将函数在某一点展开为幂级数形式，然后求导得到新的极限形式。由于泰勒展开的一阶项包含了函数的导数，因此在求导后，原始的0/0型或∞/∞型极限问题将转化为一个新的极限形式，进而可以得到准确的结果。