高分子链结构_空间构型和VSEPR模型

2024年 6月 30日上午7:43 • 激活谷笔记

高分子链结构

内旋转： $\sigma$ 键组成的单键是可以发生旋转的，因此高分子在运动时C-C单键可以绕轴旋转

构象：由于单键内旋转而产生的分子在空间的不同形态

无规线团：内旋转越自由，蜷曲的趋势越大，不规则的蜷曲的高分子链的构象为无规线团

柔顺性：高分子链能改变其构象的性质

链的柔顺性可以分为两种：

静态柔顺性
a为持续长度， $a=lexp(\frac{\Delta \varepsilon}{kT})$
持续长度越长，高分子链越刚直
动态柔顺性
持续时间 $\tau_p$ (在第五章才提到的概念)
$\tau_p=\tau_0exp(\frac{\Delta E}{kT})$
如果 $\Delta E \ll kT$ ,则说明旁氏与反式之间的相互转换的持续时间非常短，则这条链的动态柔顺性很好。

然而实际的高分子结构十分复杂，引入理想链的概念。

理想柔性链：每个相连接的键热运动时没有键角的限制，而旋转也没有位垒的障碍，每个键在任何方向取向的几率都相等，这种理想链称为自由结合链或自由连接链。

如何表征无规线团的尺寸大小呢？
可以使用均方末端距和均方回转半径

分子链一共可以分为以下几种：

自由连接链
链段是可以自由旋转的，没有键长、键角的限制，可为任意构象
链最柔时为整个链长=键长时（可以看做所有的键反复叠在一块）
因此自由连接链的均方回转半径可以表示为：
$\langle h^2\rangle_0=nl^2$
$n ：键数， l ：键长$ ，下标0表示 理想链
其均方末端距有两个特点：
(1). 均方末端距与主链中的数目n成正比
(2).末端距的分布函数是高斯函数的形式
推导需设计无规飞行问题
自由旋转链
链的旋转受到键角的限制
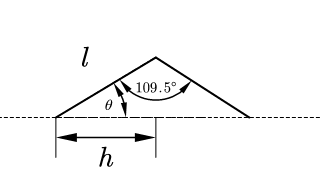
$\langle h^2\rangle_{f,r}=nl^2\frac{1-cos{\theta}}{1+cos{\theta}}$
自由旋转链伸直完全成锯齿形
Kuhn等效链
链的旋转有键角的限制，内旋转也不是自由的，而是会带动附近的链一起运动。
只要链段的数目够多，它还是柔性的，此类也称为等效自由结合链。
在Kuhn等效链中要注意，均方末端距与自由连接链的不相同，但相似。
$\langle h^2\rangle_0=Zb^2$
$L = Z b$
L指的是伸直长度，b为键长（可以与自由连接链的l等效），Z为键数（可以与自由连接链n等效）
高斯等效链
我们可以将其理解为，将一段键数为n的链段等效成高斯链段（链上任意两点的构象分布函数都呈现高斯分布）。
高斯链的根本特征在于其根均方末端距与其分子量的1/2次方成正比关系。

对于支化聚合物，随着支化类型和支化度不同，一个分子的末端距将会不同，对于环状聚合物甚至没有端点。
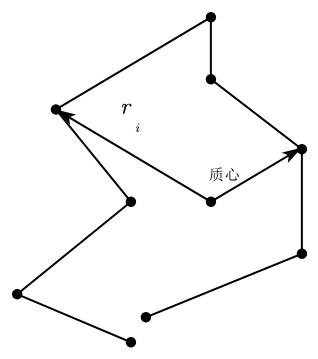
引入均方回转半径的概念：

$\langle R^2_g\rangle= \frac{\sum m_ir_i^2}{\sum m_i}$

均方回转半径与均方末端距之间存在如下关系：
$\langle R^2_g\rangle_0=\frac{1}{6}\langle h^2\rangle_0$
可通过光散射法测得

分子量越大，柔性增加，当分子量增大到一定程度时，分子量对柔顺性无影响。