Idea激活2023.1.6(2023.1)

1. Random Forest Rank

结论：一棵树的秩是 $2 imes $ 最大匹配。

这个结论其实一开始并没有发现，我考虑的是叶子节点所在的行，这一行只有它的父亲 (fa) 是 (1)；所以如果 (fa) 的儿子都是叶子，那么这些儿子随便选一行出来，其它的都变成 (0)，然后考虑 (fa) 的父亲那里，(fa) 这个位置的 (1) 也可以变成 (0)；然后我们考虑 (fa) 这个点对应的行，它要么给父亲那一列，要么给一个儿子；显然给儿子（这个儿子一定是叶子）会更加优秀。然后我们发现这个过程实质上就是在寻找最大匹配。

然后变成了期望最大匹配数；考虑线性性，我们对每个点 (u) 设一个 (f(u)) 表示仅考虑 (u) 子树内，(u) 这个点在最大匹配数上的概率，则显然有：

时间复杂度 (O(n))，求逆这里 (O(log)) 求也是可以的。

记录

2. Cycle sort

我们将重新排好序的序列设为 (b)，首先所有 (a_i eq b_i) 的位置都需要被移动到一次；所以令 (cnt=sum a_i eq b_i)，那么有解的必要条件是 (sge cnt)。

我们猜测一定有一组解可以满足 (s=cnt) 的限制，构造是容易的：我们随便拿出一个 (a_i eq b_i) 的位置，那么 (a_i) 这个数该放的位置应该是一个区间 ([l,r])，我们忽略掉 (a_i=b_i) 的那些位置，然后随便挑一个剩余位置出来（显然一定会有至少一个），然后把这个位置也标记成已使用。重复这个过程，最后我们的操作会形成若干环。

研究样例 (1)，会发现其实还有一种构造方式：第一个环 (1,4)；第二个环 (2,3,5)。但是最优解却可以直接把他们拼起来。

我们直觉上可以意识到这个原因：因为会有许多相同的数，这里的选择是不确定的，不同的选择方式会导致不同的结果。

令 (p_u) 是环上 (u) 换到的位置；我们会发现：如果两个环中分别有 (i,j) 且 (a_i=a_j)，那么我们可以通过交换 (p_i,p_j) 来合并这两个环。

这样我们得到了 (s=cnt) 情况下一定最优的解。对于更一般的情况，我们是否还能合并更多的环呢？

手玩以后，我们会发现，如果有 (k) 个环，我们从每个环中各挑一个位置出来，把他们 cycle shift 一下，然后这 (k) 个环可以合并成一个。

换言之，我们可以花费 (k) 的额外步数，创建一个新环，合并原先的 (k) 个环。显然这个操作只会在 (kgt 2) 的时候做一次，特判一下即可。

时间复杂度 (O(nlog n))。

记录

3. Koxia and Sequence

神题。

注意到 (n) 个位置并无本质区别，因此我们重新定义一个序列的权值是 (a_1)，然后求所有好序列的权值 xor 结果；设结果为 (S)，真正的答案是 (S) xor 上 (n) 遍；所以当 (n) 是偶数的时候答案为 (0) 否则答案为 (S)。现在考虑求 (S)。

考虑 or 的限制就是钦定了哪些位必须出现，且仅有这些位可以是 (1)；我们考虑容斥：枚举一个 (y’subseteq y)，然后钦定只有 (y’) 的位可以是 (1)，但不强制要求每个位都出现至少一个 (1)，也就是 or 的结果 (subseteq y’)，注意到 xor 意义下加法减法全部变为了异或运算，所以相当于我们枚举 (y’)，然后求所有代数和是 (X)，or结果 (subseteq y’) 的好序列的 xor 结果。

然后考虑拆位，枚举 (i)，我们强制 (a_1) 的第 (i) 位是 (1)，然后对所有 good 序列求和，也就是此时如果有 (a) 个 good 序列，当且仅当 (a) 是奇数的时候，我们给答案的第 (i) 位 xor 上 (1)。

考虑这个计数也就是模 (2) 意义下进行的，求：(sum_{x_1+x_2+…+x_n=X}[x_1 subseteq y’-2^i]prod_{i=2}^{n}[x_i subseteq y’])。

这个式子看上去非常的复杂，一个入手点是我们只关注它的奇偶性，加上子集的这个约束，容易联想到 Lucas 在 (p=2) 情况下的一个结论：(dbinom{n}{m}=1 Leftrightarrow msubseteq n)；换言之上面的式子可以改写成在模 (2) 意义下求：

此时 (n) 个组合数的卷积显然可以用范德蒙德恒等式优化：也就是求 (dbinom{ny’-2^i}{X}) 的奇偶性！

因此我们在 (O(ylog y)) 的时间内解决了这个问题。

记录

4. Koxia and Bracket

神题神题。

结论：任何方案下，删除的所有 一定在删除的所有 左侧。

我们考虑扫描前缀和，碰到第一个前缀和 (=-1) 的位置，这个位置一定是 ，且我们无论如何必须删除它（或者更前面的一个右括号），重复下去，我们会必须删掉若干个右括号来保证前缀和非负；任何一个删除的右括号前面都不能再删除左括号，否则我们还得额外删除右括号去重新满足前缀和非负的位置。

找到前缀和最小的位置 (p)，则 ([1,p]) 只删除右括号；((p,n]) 只删除左括号。我们容易发现两个问题是本质相同的。因此我们转为只删 的情况。

我们称一个位置 (i) 是 special 的当且仅当 (i=0)，或者 (sum_i=sum_j-1)，(j) 是上一个 special 位置。若 (le i) 的 special 位置有 (k) 个（不含 (0)），则我们就要删除 (ge k) 个在 (i) 之前的右括号。

此时考虑 dp：设 (f(i,j)) 是处理完前 (i) 个右括号以后还有 (j) 个多余删除的右括号没有被 special 位置匹配上，则 (dp(n,0)) 就是答案。

如果 (i) 是 special 位置，那么 (f(i-1,j)) 转移到 (f(i-1,j)) 和 (f(i-1,j-1))（分别对应了我们删除 (i) 和不删除 (i)）；否则，转移到 (f(i-1,j)) 和 (f(i-1,j+1))（分别对应了我们不删除 (i) 和删除 (i)）。

考虑优化：如果没有 special 位置，那么 (f(i) ightarrow f(j)) 的贡献可以用卷积形式描述。当 (kge j-i) 时，(f(i,k) ightarrow f(j)) 的贡献是不受 special 位置影响的，因为设这一段有 (cntle j-i) 个 special 位置那么 (k-cnt) 是恒非负的，直接 (f(i,x) imes dbinom{j-i}{y} ightarrow f(j,x+y-cnt)) 即可。

现在考虑分治 NTT。当递归到区间 ([l,r]) 且前面传入了多项式 (f) 的时候：

• 设区间有 (cnt) 个 special 位置，把 (f) 中次数大于等于 (cnt) 的项取出来卷积。

• 把 (f) 中次数小于 (cnt) 的项传入 ([l,mid]) 得到返回结果 (res)。

• 把 (res) 传入 ((mid,r]) 得到新的 (res)。

• (res) 和卷积结果相加即为答案。

显然只需要证明任意时刻传入的多项式 (f) 是 (O(len)) 级别的就能证明复杂度是 (O(nlog^2 n)) 的。

我们考虑归纳：如果传入的 (f) 是 (O(len)) 级别的，则递归进入 (l,r) 的多项式一定是 (O(len)) 级别的：首先递归进 ([l,mid]) 的多项式是 (O(len)) 的，跑完以后多项式次数最多增加 (mid-l+1) 次，此时传入 ((mid,r]) 的多项式依旧是 (O(len)) 的。

记录

P.S. 这个 dp 看上去很神阿，但是那个约束看上去很眼熟，仔细一想其实就是在做括号匹配阿…. 我们额外删去的是“左括号”，special position 是“右括号”，是我 naive 了…

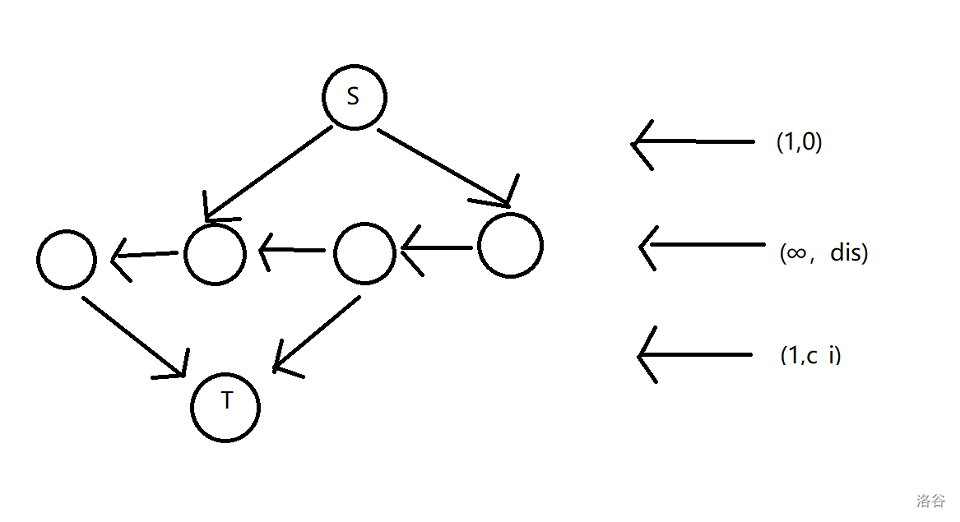
5. 旅行者

很神的一个题。

我们先考虑随机分组 (A,B)，然后连 (S ightarrow A,B ightarrow T)，这样可以求出 (S) 内一点到 (T) 内一点的最短路。

考虑我们要分若干次保证任何两个点 (i,j) 至少有一次在不同的组里。

两个不同的数至少有一位二进制不同，所以我们枚举第 (i) 位，每次按照这一位的值来分组，然后跑最短路即可。

时间复杂度 (O(nlog^2 n))。

记录

6. Guessing Permutation for as Long as Possible

很 AGC 的题。

首先，如果有 (P_ilt P_j) 则我们连 (i ightarrow j)，则整个过程相当于给这张完全图的每条边按顺序定向加进去。

如果我们当前加入 ((x,y))，那么在加入这条边之前，(x) 不能走到 (y)，(y) 也不能走到 (x)。

只要满足上面的条件，我们的图是不可能出现环的；在此基础上，更进一步地，任何一个符合上面条件的图都和一个排列一一对应。

现在我们来对符合条件的图计数。容易观察到一个必要条件是对于每个三组 ((x,y,z))，如果 ((x,y) (y,z)) 出现的比较早，那么 ((x,y)) 和 ((y,z)) 之间需要有一些约束（具体要看三者之间的关系，来判断到底是两个边的方向必须相同还是必须不同，方向是说从编号小的连到编号大的或者反之）。我们试图证明这个三的约束也是充分的。

考虑若有一个不合法的 (k(k>=4)) 结构：也就是 (v_1 ightarrow v_2 ightarrow … ightarrow v_k) 已经有边，且我们这次询问 ((v_1,v_k))。

考虑边 (v_1 ightarrow v_{k-1})，分类讨论：

• 若在刚要加入 (v_1 ightarrow v_k) 前此时还没有加入这条边，则 (v_1 ightarrow … ightarrow v_{k-1}) 必定是一个 (k-1) 的不合法结构。

• 否则，考虑 (v_1 ightarrow v_{k-1} ightarrow v_k) 构成了一个三不合法结构。

因此一个 (kge 4) 不合法结构总能导出一个 (k-1) 的不合法结构，或者是三的不合法结构，总而言之，任何 (kge 4) 的不合法结构都必定有一个三不合法结构存在。因此，反过来，当我们不存在任何三不合法结构的时候，一定不存在任何的 (kge 4) 的不合法结构。

现在的问题变成了有 (dbinom{n}{2}) 个变量，取值可以是 (0/1)，有若干个约束，形如 ((x,y)) 两个变量的值必须相同/不同，问合法解数目。

这是经典的带权并查集维护问题，时间复杂度瓶颈在于枚举所有三组，是 (O(n^3)) 的。

记录

7. Only Once

根据对称性，我们只关注 (S_1) 的和，最后 ( imes n) 即可。

任何局面下，一个点能走到的点，构成一个 ρ 的形态。

我们忽略收尾处的那条边，然后枚举说，这个 ρ 除了点 (1) 还有 (i) 个点，选点数量有 (dbinom{n-1}{i}) 种，排列方式是 (i!)，因此有 ((n-1)^{縛line{i}}) 种方案数。然后加入收尾边，也就是说会对 (S_1=1sim i) 都造成这个 ((n-1)^{縛line{i}}) 的贡献。然后剩下的 (n-1-i) 个点的连边是无所谓的。

所以预处理下降幂以及 (n^{0sim n-1}) 就可以在 (O(n)) 的时间内解决本题，且不需要求逆。

记录

8. Arrange Your Balls

我觉得是很神的构造啊，比A、C都难，怎么大家都能秒的。

设有 (k) 种颜色出现，当 (k=1) 的时候答案为 (0)；否则我们总有上界 (k)：直接把相同颜色的放一起即可。

观察样例发现有取到 (k-1) 的解，我们试图证明 (k-1) 是答案下界。

若答案里有 ((u,v)) 则连 (uleftrightarrow v)，显然 (k) 个点最后必须是联通的那么必须有 (k-1) 条边要存在。

现在就来考虑什么时候可以取到 (k-1)，根据上面的讨论这个图构成一棵树。

一个想法是我们直接 dfs，这样的话每个颜色会出现 (deg_i) 次然后对数还是 (k-1) 的。

注意到这里你还可以让我们的位置停留在原地若干次（对应到原序列就是连续的几个相同的数），所以应该有 (degle cnt) 就行。

对于任何一个正整数序列 (b_1,b_2,…,b_k) 且 (sum b=2(k-1)) 都可以构造出一个树使得 (deg_i=b_i)，构造方法就是不断拿最小的点（度数一定是 (1)）和最大的点去连边，然后删了那个叶子。

所以只要 (sum cntge 2(k-1)) 那么就一定可以构造出一个树，也就是 (ans=k-1)，否则直接就是 (ans=k)。

时间复杂度 (O(nlog n))。

记录

9. Weighed Tree Radius

结论：重新定义 (d(u,v)) 是两点的路径长度 + 两端点权值，则直径除以 (2) 上取整就是答案。

我们可以同样地考虑分为两部分：也就是说先对在路径上的点证明有上界，再证明路径以外的点都取这个值作为答案下界。最后我们会发现根据两点的距离和权值差的关系，答案要么是除以二上取整；要么是最大的 (a) 本身，如果我们将 (d(u,u)) 也纳入考虑，则可以规约为找最大直径。

这个东西也是可以套用可合并性的：我们对每个点 (u) 单独挂无数个（其实两个就够了）虚点出来，边权为 (a_u)，就可以证明这件事情。（只要是能转成非负权树上的朴素距离就都可以套这个结论）。

然后就可以直接线段树上维护了，时间复杂度 (O(nlog n))。

记录

10. Snuke the Phantom Thief

枚举个数 (cnt) 然后两个维度分别可以转成若干个形如：坐标 (le pos) 的要选 ([L,R]) 个这样的约束。

考虑这样做：S->第一维约束->点->第二维约束->T。

显然前后两部分建图应该是类似的。

我们对坐标 (1sim 100) 分别再开点，如果 (le i) 的至少要选 ([L,R]) 个，那么 (i+1 ightarrow i) 连 ([L,R]) 容量的边。最后 (x_i ightarrow i ightarrow y_i) 连边，随便选一条给费用，其它都给零费用。问题变为有源汇上下界最大费用可行流，到这里就做完了。

记录

11. Roughly Sorted

感觉看上去水实际想想还是思维很高的题。

首先考虑研究一个排列 (P) 怎么还原，我们考虑其逆序数组的变化，显然如果 (P_igt P_{i+1}) 我们交换以后，逆序数组的相邻两个位置也发生了交换，且前面的那个 (-1)。

显然我们每次选最前面的不合法的位置继续向前交换就能顶到操作下界也就是 (sum_{i=1}^nmax{0,Q_i-k})，其中 (Q_i) 是逆序数组。

问题就在于后面的位置可能把前面已经合法的位置继续往后换，这个就让统计变得比较麻烦。

我们不妨对逆排列计数，逆排列也有其逆序存在，具体地，我们可以定义 (Q_i) 是值为 (i) 的素前面有几个比它大的，一次操作 (P_igt P_{i+1}) 后，令 (x) 是操作前的 (P_{i+1})，则我们只不过是让 (Q_x) 减去了 (1)，我们发现此时 (Q) 数组的定义是无关什么位置的（因为下标的意义是值），我们实质上可以看成这样一个过程：就是选一个 (Q_igt k) 的 (i) 并让 (Q_i) 减去 (1)，这个过程就比上面明了多了！

所以一个 (Q_i) 最后会变成 (min{Q_i,k})，对于最后 (Q_ilt k) 的位置我们不用管，(Q_igt k) 的不可能出现，对于 (Q_i=k) 的，初始的 (Q_ige k) 就可以，又因为 (Q_iin [0,n-i]) 所以最后答案即为 (prod_{i=1}^{n}[Q_i=k](n-i-k+1))，瓶颈在于求 (Q_i)，时间复杂度 (O(nlog n))。

记录

12. 旅游博主

题意：给出 (n) 点 (m) 边连通图，定义一条路径（一条边不能经过多次）的权值是经过的边中的最大权+最小权，对于 (iin [2,n])，求 (1 ightarrow i) 的最短路。(n,mle 3 imes 10^5)。

考虑一个弱一点的问题：我们让最小权最小（注意一条边不能经过多次），那么考虑 (1 ightarrow i)，有些边是必须经过的。事实上，考虑对 e-DCC 缩点，则树上 (1 ightarrow i) 路径上的所有边都必须经过。

对于每个 e-DCC，类比 v-DCC 中任意 ((u,v,w)) 存在 (u ightarrow w ightarrow v) 的 vertix-simple 路径这个结论，我们有：对于任意的两点 ((u,v)) 以及其 e-DCC 的一边 (e)，存在 edge-simple 路径 (u ightarrow v) 且经过边 (e)，证明不会，纯猜的。

这样的话只要 (O(n+m)) 对 v-DCC 缩点就可以求答案了。

现在考虑更强的问题，我们不难想到：枚举 (max=k)，保留所有 (wle k) 的边，此时变成了只关注最小值的问题。这样的话我们得到了一个 (O(m^2)) 的解法。

考虑我们从小往大加边进去，则每次会把树上的若干个点缩成一个点，而如果我们加入一条边，其两端点已经在一个 e-DCC 中，这条边一定是无意义的；显然有意义的边不超过 (O(n)) 条，首先全部找出这些边，然后再重新跑一遍 (O(m^2)) 的做法，此时我们得到了 (O(n^2)) 的做法，结合一些特殊性质在原题可以拿到除了最后一个 subtask 以外的所有分数。

首先我们每次不用显式地缩点，这样非常麻烦；只需要开并查集，将深度最浅的作为代表，然后把 (u ightarrow v) 路径上的点用并查集合并在一起即可。

然后，任意时刻一个设我们枚举到的阈值是 (k)，在 mst 上 (1 ightarrow u) 的最大值是 (M)，我们加入一条非树边后其所在点的代表是 (p)，内部最小边权是 (w)，则所有 (uin subtree(p)) 都会执行：(ans_u) 和 (max{k,M}+w) 取 (min)。

这个过程可以离线下来然后在 dfs 过程中维护，为了拆开 (max) 我们只需要维护两颗线段树，一颗维护 (M+w) 一颗维护 (w)，离散化后可以做到 (O(mlog m))。

13. Merge Triplets

首先如果有 (P_igt P_{i+1}) 那么我们会发现这两个数一定是捆绑在一个序列里的。

如果我们把连续递减段划分出来那么每段的长度不能超过 (3)。

对于 (len=3) 还有一种特例，也就是 (3,1,2) 这种形态。

重新审视以后我们发现不是“连续递减”划分，而是按照前缀 max 划分。因为如果 (P_igt P_j) 且 ((i,j)) 中的每个数都 (lt P_i) 那么 ([i,j]) 一定是捆绑在一起的。

而且每一段的开头是严格在递增的。

但是这依旧不是充要条件。考虑一个长度为 (3) 的序列，有 (3/1+1+1/1+2/2+1) 这些拆分方式，不管怎么说 (2) 的个数 (le 1) 的个数，当其成立的时候，我们一定能反向构造出一组分配序列的方案，此时充要条件就是每一段 (le 3) 且 (cnt_2le cnt_1)。

如果确定了划分方式，我们的计数还有一个若干个钦定 (a_i) 是前缀最大值的约束，总方案数是 (frac{n!}{prod_{a_i}})，这个就从最大的 (a_i) 开始倒着去掉不合法的填数就行。

但是任意模数就不支持求逆了，所以我们不是考虑除掉多少，而是把 (a_i) 以外的数乘回去。

具体地设 (dp(i,j)) 是 (1sim i) 填完 (cnt_1-cnt_2=j)，那么 (dp(i,j) ightarrow dp(i+1,j+1),dp(i+2,j-1),dp(i+3,j))，系数分别为 (1,(i+1),(i+1)(i+2))。

时间复杂度 (O(n^2))。

记录

14. Yet Another ABC String

好牛逼的数数。

首先我们考虑容斥，也就是指定若干 ({p_i}) 满足 (p_ip_{i+1}p_{i+2}) 是不合法的。

我们很容易发现如果我们把 (p_i) 看作一个 ([p_i,p_i+2]) 的这样一条线段，如果两条线段有交，那么方案数就变的不是那么的自由。

因此我们考虑每条极长的线段，设为长度 (n)，那么任意两条线段都是不交的，我们可以说钦定一些线段 (L_1,L_2,…,L_k)，现在我们来考虑每条线段内部的容斥系数：其为所有覆盖这条线段的，选择 (p) 的方法的 ((-1)^{cnt}) 之和。显然 (f(3)=(-1),f(4)=1)，考虑更一般的 (f(n))，首先我们必须在 (n-2) 处放一个 (p) 来覆盖 (n)，然后考虑剩下的所有长度为 (3) 的小线段，至少有一个结尾处是在 ([n-2,n-1]) 这个位置的，也就是有 (f(n)=(-1)(f(n-1)+f(n-2)))。最后得：

上述定义都是在 (nge 3) 前提下的，我们发现可以拓展到 (nge 1)，因为那些没有被 (p) 影响到的位置它们的容斥系数显然就是 (f(1)=1)。然后我们就把整个长度为 (n=a+b+c) 的序列划分成了若干条线段且每条线段的长度模 (3) 的余数都不为 (2)。

我们考虑，如果划分确定的情况下，怎么算填 (a,b,c) 的方案。

对于长度是 (3) 的倍数的线段，那么 (a,b,c) 的数目相等且我们只需要决定开头的一个字符就好啦，加上容斥系数的影响所以贡献是 ((-3))；否则，有一个字符是恰好比其它两个多出现一次的，而且它应该就位于这条线段的结尾，当我们枚举了这个字符究竟是多少以后，贡献就是 (1)。

现在考虑一般情况，首先枚举长度不是 (3) 的线段的条数设为 (x)，则我们一定能求出这 (x) 条线段里，分别有多少条，他们的特征字符（多的那个）是 (a,b,c) 的，设为 (ca,cb,cc)，那么忽略其它素，排布这 (x) 个素的方案数是 (dbinom{x}{ca,cb,cc})，然后我们考虑在 (x+1) 个空位里插入剩下的 (n-x) 个素，每个空位里的素数量都是 (3) 的倍数，所以我们不妨设 (rest=(n-x)/3)，那么就是把 (rest) 个素（长度为 (3)）分配进去。

考虑形成的结构有两种：

1. (m) 个长度为 (3) 的素，而且后面还有一个代表字符（也就是枚举的那 (x) 个之一）。

2. 只有 (m) 个长度为 (3) 的素（也就是每种方案里，最后一个空对应的那一段）。

我们先来看第二种情况，问题变为把 (m) 划分成若干段，设划分成了 (cnt) 段则答案加上 ((-3)^{x})。容易列出 dp 方程：(g(n)=sum_{mlt n}(-3)g(m))，边界 (g(0)=1)；通过归纳可以得出当 (nge 1) 的时候有 (g(n)=(-3)(-2)^{n-1})。

情况 (1) 是类似的，只不过我们每次是从 (m) 个素里选出前 (k) 个，后面的 (m-k) 个会和那个代表字符合并，所以它的贡献是 (g) 的前缀和，通过归纳也可以发现是 ((-2)^{m})。

所以我们枚举两种情况：也就是最后一个空到底放不放素进去，对两种情况分别计数都是容易的：因为不管怎么塞素，我们只关注塞的素的总数目。

时间复杂度 (O(n))。

记录

15. Giant Graph

好牛逼啊我草，不是这是怎么想到的 idea。

首先权值的形式是 (w^{(x+y+z)}) 而 (wgt n^3) 所以我们会贪心地把当前 (x+y+z) 最大的点选了，如果有多个我们注意到他们之间不可能互相影响（至少有两个维度的坐标是不一样的），所以从大往小枚举 (x+y+z) 的值然后判断，这样我们得到了一个 (O(n^3)) 级别的做法，而且容易看出答案是唯一的。

然后就不会优化了……

我们把 (x+y+z) 小的往大的连边，则一个点 ((x,y,z)) 能选当且仅当其所有后继不被选；一个点不被选当且仅当后继至少有一个被选。

这个定义和博弈论中必败必胜态的定义一模一样……

而且我们每一步只会变动一个维度，所以可以把三个维度看作三个独立的 dag，((x,y,z)) 是描述在三张图上的位置的，操作是每次选择一个图的棋子移动一格。

这就是我们非常熟悉的典中典 sg 题了，根据上面的结论 (sg_xoplus sg_yoplus sg_z=0) 的时候我们才会把 (w^{x+y+z}) 加入答案。

到这里就是 fwt 一手完事了，但是 sg 还有一个结论在，就是 (m) 条边的 DAG 上构成的 sg 不超过 (O(sqrt m)) 所以最省事的写法是直接 (O(msqrt m)) 暴力卷积就做完了，当然如果我们做两次卷积那就直接 (O(m)) 啦。

记录

16. 种树

其实是个很著名的基础反悔贪心题，学习了一点模拟费用流，感觉用这个角度更加直观，泛用性也更强。

考虑建立费用流模型来解决这个问题，难点在于不能同时选相邻的两个。

对 (n+1) 个间隔（包括最两侧）建图，$S ightarrow $ 奇数 $ ightarrow $ 偶数 ( ightarrow T)，每个奇数间隔向相邻的偶数间隔连边，边权为两个间隔的公共点的 (c)。

这个正确性不难证明，我们考虑快速优化这个过程。

由于这是一张静态图所以任何时刻不会出现负环，我们只需要时刻考虑寻找增广路即可，考虑任意时刻增广路首先从 (S) 出发到达一个奇数间隔，结束的时候从一个偶数间隔走到 (T)，过程中会在中间这部分折返。由于中间部分的边都是在相邻的间隔之间连的，我们会发现对应在原序列上就是选一段使用状态交错（且首尾必定未使用）的区间并反转其状态。

设 (U) 是这样的一个合法区间，首先 (U) 的任意子区间都不可能是合法区间。因此我们可以把原序列唯一地划分成若干个合法区间。考虑一次操作如若反转了区间 (x) 的状态，则其会和两边两个区间进行合并。因此我们用 pq 维护当前所有区间，同时用链表维护相邻关系即可做到 (O(nlog n))。

记录

17. Olympiad in Programming and Sports

考虑建出费用流模型，$S ightarrow $ 人 $ ightarrow $ 两个属性点 ( ightarrow T)，费用在人到属性点这部分。

首先属性点只有 (2) 个肯定是重要性质，由于这还是静态的图所以我们依旧只考虑增广路。只有两种类型：直接 (i ightarrow u ightarrow T)，还有一种是 (i ightarrow u ightarrow j ightarrow v ightarrow T)，(u,v) 分别代表两种属性点。

第一种也就是我们直接把一个没选的老哥放进 (1/2) 里；第二种是说我们把一个没选的老哥放进 (1)（还有一种对称情况不再赘述），从 (1) 里取出一个老哥放进 (2) 里。

我们分别维护：所有没选的老哥的 (a/b) 最大值，以及进入 (1) 的老哥的 (b-a) 最大值还有进入 (2) 的老哥的 (a-b) 最大值即可。时间复杂度 (O(nlog n))。

更一般地，如果有 (k) 个属性点，则我们可以在 (O(k imes 2^k imes nlog n)) 的时间内解决。

记录

18. 跳伞求生

老鼠进洞的模型三。也就是我们把所有人按照 (a)（或者 (b)）排序以后，相当于每个人只能想左走，而收益是距离加上对应的洞的 (c)。

考虑建立费用流模型：

我们按照顺序依次加入人和洞：因此我们既需要寻找增广路，也需要消圈。

考虑如果增加了一个人：

• 增广路：很显然，就是 $S ightarrow $ 这个人，然后向左走若干步，再到 (T)。

• 消圈：考虑我们新增的边只有一条 (S ightarrow u)，那么可能出现的正圈也就是形如 (S ightarrow u) 然后向左走到某个点 (v) 然后走回 (v ightarrow S)。

如果增加了一个洞：

• 增广路：很显然，没有新的增广路出现，因为没有人能到它…

• 消圈：这条 (u ightarrow T) 的边同样也没有办法进入一个，因为此时残量网络上不存在某个点的终点是 (u)。

现在来考虑增广路和消圈如何维护：对于增广路，也就是找到一个 (c-y) 最大的未被选择的洞；对于消圈，也就是找到 (x) 最小的被使用的人，用两个堆即可维护，时间复杂度 (O(nlog n))。

记录

19. Bracket Insertion

首先我们把这个动态的过程转变为静态的过程：我们给 (2n) 个字符分别打上一个 label，要求：

• 每个 label 恰好出现了两次，且两次对应的字符是不一样的。

• 不同的 label 之间只允许嵌套，不允许交叉，也就是不能出现 ( ext{1212}) 这样的类型。

• 外层的 label 一定小于内层的 label，也就是我们只允许 ( ext{1221}) 而不允许 ( ext{2112})。

设有 (cnt) 个 label 是先出现左括号再出现右括号的，则它出现的概率是 (p^{cnt}(1-p)^{n-cnt} imes (prod_{i=0}^{n-1}(2i+1))^{-1})，把后面的常数先提出来。

设 (f(x,y)) 是 (x) 次操作得到一个字符串，且其最小前缀和取到 (-y) 的所有情况的概率和，考虑转移，考察第一个字符和其匹配的字符，设分别在 (1,i) 处，则我们考虑 ((1,i)) 处和 ((i,x]) 处，由于性质 (2)，它们是互相独立的，若 (1 – i) 这组匹配先出现左括号，设左边 ((1,i)) 和右边 ((i,x]) 的最小前缀和分别为 (a,b)，则此时的最小前缀和就是 (min(max(a+1,0),b))，否则为 (min(a-1,b))。这里由于我们在实现的时候取相反数了，所以 min，max 的意义应该互换。

注意到其形式极其接近 (f(a,x) imes f(b,y) ightarrow f(a+b,max{x,y})) 这个形式，只需要对每个 (f(x)) 维护其前缀和即可做到 (O(n^3))。

最后还要注意我们要乘上一个组合数系数，表示从 (x) 种颜色里选出一些分别左半边，剩下的分给右半边的方案数。

记录

20. Sum of Sum of Digits

Lemma 1：当 (max(A)le 1) 的时候，原问题在 (x=0) 处取最优解 (sum(A))。

对于 (A_i=0) 显然 (x=0) 最优，对于 (A_i=1)，不管 (x) 取多少，它至少产生 (1) 的贡献，所以 (sum(A)) 为下界，且它一定能在 (x=0) 时取到。

Lemma 2：(xlt 10^9)。

由于 (A_ile 10^9)，所以第十位上它们都为 (0)；我们从低位开始确定 (x)，则确定了前九位以后，考虑进位，那么有若干 (A_i) 的第十位是 (1)，其余是 (0)；此时根据 Lemma 1，我们取 (x=0) 最优秀，也就是第十位开始的 (x) 都只能填 (0)。

Lemma 3：当确定了前 (k) 位的 (x) 以后，如果我们把初始的 (A) 按照前 (k) 位降序排序，则在 (k+1) 位产生进位的永远是一段前缀。

这里我场上 naive 了，以为只有 (k=1) 成立，所以错失了一个很关键的性质。

现在考虑设计 dp：设 (f(i,j)) 是确定了前 (i) 位（从低位开Idea激活2023.1.6始），然后在第 (i+1) 位产生进位的是排序后前 (j) 个的答案。

注意到这个 dp 是从 (f(i+1)) 转移到 (f(i)) 的，初始化是 (f(10,j)=j)。

考虑转移，我们从 (f(i,j)) 转移到 (f(i,j+1))，这样就会每次修改一个数，然后我们设 (cnt_j) 是第 (i+1) 位是 (j) 的数的个数（由于进位的存在可能为 (10)）。

则设枚举的 (x) 的这一位是 (r)，我们有 (r+cnt_jge 10) 的位置都产生进位。只要从小往大枚举 (r) 即可统计贡献。

令 (K=10)，则本题复杂度大致在 (O(K^2N)) 级别。

记录

21. Eat Them All

考虑这个 (n=3) 的限制极为显眼。事实上求的是一个类似哈密顿路的东西：我们考虑对每条边 (u ightarrow v) 钦定它的出现次数，然后把问题变成一个欧拉回路问题。

事实上共有 (24) 条有向边；欧拉回路存在的充要条件是弱联通+度数限制；度数的话首先要求每个点出入度平衡，同时还钦定了出度的具体值，容易联想到网络流。那么我们只需要满足弱联通这个条件，换言之枚举一颗生成树即可：钦定这些边的出现次数至少是 (1)，总方案数是小于 (dbinom{24}{8}) 的，实际跑下来不超过 (10^5)。

当确定了弱连通的条件后，用网络流建图来确定每个点的度数：对每个点建两个虚点 (IN(i),OUT(i))，并且连 (i ightarrow OUT(i)) 以及 (IN(i) ightarrow i)，这两条边的流量都必须是 (a_i)。然后对于每条边 (u,v)，从 (OUT(u) ightarrow IN(v))，此时跑无源汇上下界可行流即可。

时间复杂度 O(能过)，但其实是应该非常稳的，因为这个网络流的点边都非常非常少……

记录

22. String Query

由于有在中间插入删除这个事情，所以我们考虑维护两个对顶的双端队列，然后跨越的部分可以直接哈希暴力。

现在问题变成了一个双端队列的修改，问模式串出现次数。

如果是只有一端修改的队列，可以对所有模式串离线下来建 ACAM 然后只需要一个 BIT 就可以解决。

但是如果要在前端操作那整个走到的节点都会被改变。

这里有一个双栈维护 deque 的 trick：就是说用两个对顶的栈维护（那么在本题左边的那个栈就是在反串的 ACAM 上修改了）然后就正常在栈顶修改。当一个栈被删空的时候就暴力把剩下的对半分重构。用势能的分析方法可以说明复杂度是均摊线性的（忽略其它操作）。跨越部分的还是哈希暴力。

令 (S) 是模式串长和，则构建 ACAM 的复杂度是 (O(S imes sum c))，主体部分的复杂度是 (O(qlog S + S))。

记录

23. 组合数问题

感觉，弗如 Cards 加强版……

若 (m=0) 则答案显然是 (c imes (1+x)^{n})。

注意到一般情况下，题目可以规约成对 (O(m)) 个单项式分别求答案：

现在假设 (p) 是一个 (le m) 的常数，相当于做 (O(m)) 次这个和式：

把 (i^{p}) 拆成下降幂形式：

下降幂的目的是组合数：

交换求和顺序：

内层根据二项式定理即为 (x^{j} imes (1+x)^{n-j})。

如果假设斯特林数和组合数此时都可以处理好，则对单个 (p) 计算一次的复杂度就是 (O(p))，那么计算的复杂度就是 (O(m^2))。

斯特林数可以 (O(m^2)) 地预处理出来，组合数我们只需要用到 (dbinom{n}{0}sim dbinom{n}{p})，在任意模数的情况下可以分解质因数来达到目的，一个粗略的上界是 (O(msqrt{n})) 的，完全可以通过。

记录

24. 紫荆花之恋

如果这个问题是允许离线的，则就是一个简单的点分治问题。

问题在于这个强制在线，需要我们进行动态点分树的维护。

考虑定期重构：不妨假设每 (sqrt{n}) 个点加入后进行一次重构点分树，对于不在点分树的 (sqrt{n}) 个点暴力比较。

这样构建点分树的部分是 (nsqrt{n}log^2 n) 的，而暴力比较是 (nsqrt{n}log n) 的，在点分树上的查询是 (nlog^2 n) 的。

发现前后两部分的复杂度并不平衡，换言之我们的块长并没有设到最优，把块长调到 (1300) 左右的时候这个做法会比较优秀。

如果我们能把暴力比较的部分优化到 (nB)（(B) 是块长），那么令 (B=sqrt{n}log n)，这个算法就变成了严格的 (nsqrt{n}log n)。

注意到对于每个点，在它那个时刻，到点分树的 (O(log)) 个祖先的真实距离可以在 (O(log^2)) 的时间内预处理出来。对于两个散点 ((x,y))，有两种情况：

1. 它们在真实点分树上的 LCA 也在这个定期重构的点分树上。这种情况下我们把每个点挂到其所有的祖先上即可。

2. 这个 LCA 不在定期重构的点分树上。注意所有满足条件的这些点构成一个连通块，我们只需要以当前新加入的那个点为根暴力 dfs 即可。

这样就在 (O(B)) 的时间内完成了对散点的询问，因此就做到了 (O(nsqrt nlog n))。

记录

25. Span Covering

这个是比较蠢的做法，只能做到 (O(x^3ln x))，优点在于和 (n) 是无关的。

考虑容斥，钦定若干位置不被覆盖，把序列分成了 (cnt+1) 段，且剩余部分的和是 (x-cnt)。

相当于我们确定了 (cnt+1) 个变量和，设其值为 (langle v angle)，则一条长度为 (l) 的线段的放置方法是 (sum_{i=1}^{cnt+1}max{0,v_i-l+1}) 种。

如果把这些变量排序，则任意一条线段，对它有贡献的是一个后缀。

如果把线段降序排序，从大到小去选变量的值，那么就可以边 dp 边计算了。

设 (dp(i,j,k)) 是选了 (isim x) 这些值作为变量，确定了 (k) 个变量且和为 (j) 的贡献之和，首先选择这部分要做 egf 卷积一样的东西；每次 (dp(i) ightarrow dp(i-1)) 后考虑所有长度 (=i-1) 的线段，计算它们的方案数即可。

时间复杂度 (O(x^3ln x))。

记录

26. Comfortably Numb

枚举 (max) 则左右端点取值是一段区间。

如果我们从小往大枚举 (max)，那么执行的就是一个类似不断把区间合并的过程。对每个区间维护 trie。然后我们要从两个区间分别选一个，计算完后直接合并。

那么两个量的 xor 最大值不好计算，但是可以枚举两边 sz 小的那个然后在另一边贪心。

这样的话根据启发式合并，复杂度是 (O(nlog nlog a)) 的，如果每次是暴力重新插入到另一边那么空间看上去也是这个。但注意到我们可以搞一下简单的内存回收这样就始终都是 (O(nlog a)) 级别的空间了。

记录

27. みんな仲良し高橋君

首先考虑如果给出 (2N) 个点怎么 check。

对行列建出二分图，((x,y)) 就连 (L(x)leftrightarrow R(y))。

结论：如果每个连通块的边都有偶数条，那么就一定能构造。

这显然是必要条件，充分性感觉很神。等会再学习一下，学会了再来。

然后就变成一个很简单的题了：首先奇数条边的连通块有且只能有一个，我们只能删掉其中的一条边。如果不是割边可以随便删。割边的话一遍 dfs，求出 dfs 树的子树内边数，就可以根据其奇偶性判断。

时间复杂度 (O(n))。

记录

28. Reverse and Inversion

很高妙的题。

首先，问题可以视作求 (m) 次操作后序列权值的期望。

一个直观的想法是我们对于每个 (ilt j) 研究 (P_igt P_j) 的概率，但这其实是不可做的，如果走入这个误区就很难出来。

把 (i-j) 这个贡献拆开，设 (g(i)) 是以 (i) 结尾的逆序对个数减去以 (i) 开头的逆序对个数（这里的 (i) 是指位置），则显然答案为 (sum_{i=1}^{n}ig(i))。

结论：(g(i)=i-p_i)。

我们设 (i) 前面的部分，小于和大于 (p_i) 的分别为 (x_1,y_1)；后面部分设为 (x_2,y_2)，则 (x_1+y_1,x_2+y_2,x_1+x_2,y_1+y_2) 可以列出一个四方程组，且等式右侧只含 (i,p_i)。因此只要确定了 (i,p_i)，那么 (g(i)=y_1-x_2) 就一定能求，事实上最后解这个方程组容易解出 (y_1-x_2=i-p_i)。

因此现在要求的也就是 (E(sum_{i=1}^{n}i(i-p_i)))，实质上真正的难点在于求：(E(sum_{i=1}^{n}i imes p_i))。

如果直接用线性性拆开，则我们不好研究每个位置最终的值。这种情况下我们考虑反过来：对每个数求其最终位置的期望，设为 (E_i)，则那个期望等价于 (sum_{i=1}^{n}p_i imes E_i)。

结论：只要一个位置被操作了，它的期望位置一定是 (frac{n+1}{2})。

这个高妙结论实质上只需要有一个很显然的事实导出：就是如果 (i) 被操作了，它到 (j) 和 (n-j+1) 的概率是均等的。

因此我们只需要分别计算一个位置一次都不被操作的概率，和其补。然后期望位置就分别是 (i) 和 (frac{n+1}{2})。

计算概率的部分单次需要 (O(log m)) 时间算快速幂，所以时间复杂度是 (O(nlog m)) 的。

记录

29. Tri-Colored Paths

神神神。

就是说只要把环考虑清楚就结束了。

首先考虑容斥，不妨考虑不合法的方案数。

如果一个环有三种颜色，是否一定有解？

我们发现并不，特殊情况是一个三环，此时由于是 vertex-simple 的路径，并不能把三条边都走了。

另一方面，如果这个三环还连出去了一些边，是否又会出现解。

我们会发现一个反例：如果只有一个点和外界有连边，设是 (a) 点，那么当且仅当外界的所有边都被设置成了边 (b-c) 的颜色，此时才会无解。

如果有至少两个点和外界有连边，如果它们连到不同的点上，会发现无论怎么样都会出现解；但是压力来到一种特殊情况：两个三环共用一条边，但此时只要确定一个三环则另一个三环唯一确定，且我们发现如果这个结构任意在多和一个外界点连边，弗论颜色，都会有解。

换言之，当 (nle 4) 的时候可以暴力，(nge 5) 的时候，不合法的结构只会出现一个最多一个三色三环，且这个三环只有一个点和外界相连。

设找到的这样的三环有 (k) 个，则这部分情况贡献 (6k) 的方案数。

现在考虑任何一个环的颜色都是 (le 2) 的情况。

容易发现如果任何一个环的颜色都是 (1) 看上去就长的很好，比如一个点双内的边都会是颜色相同的；所以我们试图去说明颜色 (=2) 的环不会存在；但它肯定会存在，如果想避免它，就只能说明其一定能归约到出现三色环的情况。

但好像这点也做不到，只要我们只染两种颜色不就好了。

如果我们强制三种颜色都出现然后计算不合法方案数（上面第一种讨论的方案数仍不变），考虑一个两色环（注意它的长度 (ge 3)），以及随便一条第三种颜色的边。

如果这条边是弦，显然会有三色路径；如果这条边至少一个点不在环上，显然也有三色路径。

然后考虑任何一个环都是单色且三种颜色都出现的情况。

根据点双的讨论我们建立圆方树！虽然一条简单路径在圆方树上并不能表示成一条简单路径，但其所经过的方点（也就是点双）是构成简单路径的（如果算上中间过渡的圆点）。

因此问题变成了给圆方树的方点染色使得任意一条简单路径没有三色，树的问题就非常好做了！

首先直接做就有个 dp 做法：设 (f(u,0/1,mask)) 是 (u) 子树有无三色路径，到根的路径颜色集合构成的形态是 (mask)。

但是这个还是有点烦，我们注意到一定是随便选一个圆点 (u) 然后把他当成根，一颗子树内的颜色一定是一样的。

这样的话其实我们不需要建树，只需要求出每个点在多少个点双内（就对应的子树数目）就做完了，跑一边 dfs 即可。

时间复杂度 (O(n+m))。

记录

30. Avoid Coprime Game

感觉难得可以自己做一个 ARC D 啊。

事实上任何时刻可以用 ((x,y)) 描述一个状态：(G=x) 且使用了 (y) 个 (x) 的倍数（包括 (x)）。

因此我们已经可以写出一个 (n^2) 级别的 dp 了。

事实上我们任意时刻只关注 (y) 的奇偶性，理由如下：

首先如果 (x) 不能变的更小则我们只通过 (y) 的奇偶性就可以判断状态。

否则 (x) 一定会变的更小：如果先手直接就让 (x) 缩小了那么这一层不需要关注 (y)；否则后手也不会想要缩小，两人轮流拉锯，也是通过 (y) 可以决定最后谁向下转移。

因此设 (f(x,0/1)) 就够了，这样状态 (O(n))，我们考虑转移总数是 (O(nln n)) 的，压力来到了检查转移合法性。

也就是说给出 (ymid x)，求是否存在 (a_i) 满足 (gcd(a_i,x)=y)。

可以对所有的 ((x,y)) 预处理，枚举 (y) 则问题变成这样一个形式：

给出一个 ([1,m]) 的子集 (S)，对于每个 (iin [1,m]) 询问是否存在 (jin S) 使得 ((i,j)=1)。

(sum m) 是 (O(nln n)) 级别的。

这个可以莫反出来，所以就在 (O(nd(n)ln n)) 的时间内解决了。

记录

31. Gosha is hunting

首先选的球肯定是越多越好，所以我们最后肯定是 (a,b) 个球都会用上。

另一方面在 (a) 个球用上的时候，(b) 类球用的越多则答案越大且增长越慢；因此考虑使用带权二分：这样就可以忽略掉 (b) 的限制。

我们明确在最优秀的前提下让使用的 (b) 类球尽可能多。则所有 (qge k) 的球首先使用 (b) 类，它们要么变成 a only 增量为 (p-q+k) 要么变成 a and b 增量为 (p-pq)；剩余的球只可能直接变成 a，增量为 (p)。

对增量排序（增量相同的时候优先考虑不取消 (b) 的情况）即可，时间复杂度 (O(nlog^2 n))，容易看出可以通过归并做到 (O(nlog n))。

实现上，规避浮点二分的手段是给所有数乘上 (10^6)，（注意最开始的 (pq) 还要额外除以 (10^6)），二分上界保证切到一个 (b) 类都不用就行，也就是 (gt 10^6) 即可。

记录

32. 林克卡特树

根据数据范围先来想一下 (O(nk)) 的做法。

题目可以转化成选择 (k+1) 条点不相交的路径（认为一个点也算一条路径），求它们权值和的最大值。

这看上去就是个很 dp 的东西：设 (f(u,k,0/1)) 是子树内选了 (k) 条路径且是否有一条是从某个点向上到 (u) 的（不继续向下）；转移的时候是设 (g(0/1/2)) 的，分别表示点 (u) 没有路径/有一条向上的/前面有一条跨越的。

这样就可以在 (O(nk)) 的时间内解决了，可以获得 60pts。

这个形式想要摆脱掉 (k) 就猜一手凸性然后使用 wqs 二分，这样就变成 (O(nlog V)) 了。如果是场上我应该写个数据分治的（（

记录

33. Idea激活2023.1.6 April Fools’ Problem (hard)

容易建出费用流模型然后说明了关于流量有凸性：是一个下凸函数。

因此 wqs 二分一手然后就没有 (k) 的限制了。

然后考虑这就是一个经典的买卖股票那个题，随便模拟费用流或者反悔贪心（本质相同）一手就解决了。

时间复杂度 (O(nlog^2 n))。

记录