（ICIP-2018）用于深度图像检索的加权广义平均池化

用于深度图像检索的加权广义平均池化

paper题目：WEIGHTED GENERALIZED MEAN POOLING FOR DEEP IMAGE RETRIEVAL

paper是日本NTT公司发表在ICIP 2018的工作

paper地址：链接

ABSTRACT

卷积激活上的空间池化（例如，最大池化或总和池化）已被证明在学习用于图像检索的深度表示方面是成功的。然而，大多数池化技术都假设每个激活都同样重要，因此它们会允许无信息图像区域的存在，这些区域在匹配方面起负面作用或导致特定视觉实例的混淆。为了解决这个问题，本文提出了一个可训练的构建块，它引导汇集对当前任务很重要的局部信息。该方法将池化定义为加权广义均值 (wGeM)，其中在激活时学习权重，反映图像匹配中每个激活的判别能力。将 wGeM 嵌入深度网络可改善图像表示并提高标准基准的检索性能。 wGeM 不需要任何边界框注释，而是从头开始学习激活的潜在概率。它甚至超越了客观性，学会了观察重要的视觉细节，而不是感兴趣目标的整个区域。

索引词——深度卷积网络、图像检索、学习排序、池化、加权广义均值

1. INTRODUCTION

微调深度网络以学习深度图像表示已被证明可以显着改善图像检索。更重要的是通过结合 1) 良好的预训练分类网络、2) 良好的池化方法和 3) 排序损失来直接优化网络与检索任务中使用的相似性。以前，使用了许多池化方法，从全连接层到全局池化方法，包括总和池化、最大池化、广义平均 (GeM) 池化、区域池化和聚合技术。这些方法中的大多数对卷积层的激活执行统一池化，其中每个激活都对全局表示的构建做出同等贡献。

然而，空间均匀池化会受到激活的影响，这些激活对匹配起负面作用或导致特定视觉实例的混淆。为了解决这个问题，Gordo 等人提出了一种区域proposal网络（RPN），该网络经过训练可以定位图像中感兴趣的对象。 RPN 学习在目标级别预测区域proposal，其中并非所有信息都对最终检索任务很重要。它还需要用于训练的边界框注释和大量的预处理工作。Kalantidis等在总和池化之前应用空间加权来提升同时发生大量强激活的位置并降低不太活跃的位置的权重。然而，他们工作中的权重层是不可训练的，并且激活强度可能与位置的判别力无关。

本文提出利用空间加权机制对最后一个卷积层的激活进行池化。这种方法预测了一个权重，该权重描述了在图像匹配和检索方面如何区分每个位置的每个激活。本文的想法受到视觉注意力的启发，视觉注意力已成功应用于图像字幕、机器翻译和目标识别。通过扩展它并将其与池化和学习排序相结合，将这种机制引入图像检索任务，从而基于一种新颖的加权广义均值 (wGeM) 池化方法实现深度表示的端到端学习。 Sum pooling、max pooling和GeM pooling都是wGeM的特例。本文的方法还推广了Kalantidis的方法，同时使加权机制可训练。与预测物体刚性边界框的RPN不同，wGeM从头开始学习激活的潜在概率。本文的方法不需要进行训练的边界框注释，不需要昂贵的预处理或任何关于训练数据集的假设。证明了将wGeM结合到深度网络中可以改善图像表示并提高标准基准的检索性能。

2. PROPOSED METHOD

2.1. Network Architecture and Learning

提出的 wGeM 可以应用于任何卷积神经网络 (CNN)，例如AlexNet、VGG和ResNet。这种经过图像分类训练的 CNN 在执行检索微调时提供了良好的初始化。给定图像 $\mathbf{I}$，CNN的输出是一个三维张量 $\mathbf{X}\in {\mathbb{R}}^{H\times W\times K}$，$K$ 是通道的数量，其全连接层被丢弃了。现在添加一个wGeM块，将 $\mathbf{X}$ 作为输入并产生一个 $l^2$ 归一化的描述符 $\overline{\mathbf{y}}\in {\mathbb{R}}^K$ 作为输出。关于wGeM的细节在第2.2节中提供。

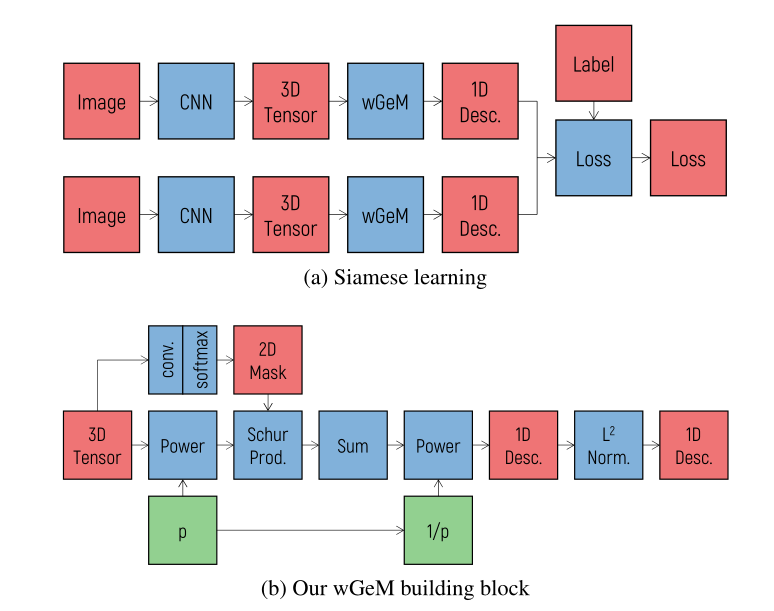
本文遵循Radenovic等人[6]关于学习程序的说法。如图1a所示，采用了一个孪生网络，其中两个分支共享相同的参数。训练输入包括图像对 $\left({\mathbf{I}}_i,{\mathbf{I}}_j\right)$ 和标签 z i , j ∈ { 0 , 1 } z_{i, j} \in\{0,1\} zi,j​∈{
0,1}，分别声明一个图像对是不匹配还是匹配。${\overline{\mathbf{y}}}_i$ 是wGeM输出的图像 ${\mathbf{I}}_i$ 的描述符。采用对比损失, 其定义为
$${\mathcal{L}}_{i,j}=\{\begin{array}{ll}\frac{1}{2}{\Vert {\overline{\mathbf{y}}}_i-{\overline{\mathbf{y}}}_j\Vert }_2^2& \text{ if }{z}_{i,j}=1\\ \frac{1}{2}{\left[\max \left(0,\tau -{\Vert {\overline{\mathbf{y}}}_i-{\overline{\mathbf{y}}}_j\Vert }_2\right)\right]}^2& \text{ otherwise }\end{array}(1)$$
其中，$\tau$ 是一个超参数，定义了铰链损失的边际，只有当欧氏距离小于 $\tau$ 时，非匹配对才会支付线性惩罚。在测试过程中，经过微调的网络为查询和语料库中的每个文档产生一个描述符 $\overline{\mathbf{y}}$。检索工作通过使用欧氏距离计算查询和每个文档描述符之间的相似度来进行。

图 1. 网络架构和 wGeM 池化。块和层以蓝色显示。变量和参数分别以红色和绿色显示。

2.2. Weighted Generalized Mean Pooling

wGeM 将张量 $\mathbf{X}$ 作为输入并产生一维描述符 $\overline{\mathbf{y}}$。令 ${\mathbf{x}}_k\in {\mathbb{R}}^{H\times W}$ 是通道 k ∈ { 1 , … , K } k \in\{1, \ldots, K\} k∈{
1,…,K} 的激活特征图。令 $N=H\times W$。重塑 ${\mathbf{x}}_k$ 使得 ${\mathbf{x}}_k={\left[x_{1,k}\dots x_{N,k}\right]}^{\top }$。为清楚起见。还假设 CNN 的最后一层是 ReLU，使得所有 ${\mathbf{x}}_k\in \mathbf{X}$ 都是非负的。

给定一串正的权重 $\mathbf{\Omega }={\left[{\omega }_1\dots {\omega }_N\right]}^{\top }$，其中 $\Vert \mathbf{\Omega }{\Vert }_1=1$，利用加权广义平均数，提出构建一个一维描述符 $\mathbf{y}={\left[y_1\dots y_K\right]}^{\top }$，形式为
$$y_k={\left(\sum _{i=1}^N{\omega }_i{x}_{i,k}^p\right)}^{1/p}(2)$$
其中 $p$ 是指数。这是wGeM的核心。每个权重 ${\omega }_i\in \mathbf{\Omega }$ 描述了激活 ${\left[x_{i,1}\dots x_{i,K}\right]}^{\top }$ 在位置 $i$ 用于将图像 $\mathbf{I}$ 与其他图像区分开来。因此，$\mathbf{\Omega }$ 可以理解为软2D掩码。 wGeM 与视觉注意力机制有关，但它与它们的区别在于指数 $p$ 的存在。描述符 $\mathbf{y}$ 稍后经过 $l^2$ 归一化，得到最终的描述符 $\overline{\mathbf{y}}$。因此，两幅图像之间的相似度变成了余弦相似度，可以用内积 ${\overline{\mathbf{y}}}_i^{\top }{\overline{\mathbf{y}}}_j$ 计算。对于广泛使用的CNN，$K$ 等于 512 或 2,048，使 $\overline{\mathbf{y}}$ 成为紧凑的图像表示。

继 Radenovic 等人[6]之后，学习指数 $p$ 以及 CNN 的微调。考虑一个函数 $\Phi :\mathbf{X}\mapsto \mathbf{\Omega }$，它通过将 $\mathbf{X}$ 转换为关于是否将位置 $i$ 处的激活编码到 $\mathbf{y}$ 的灵活决策来参数化 $\Omega$。与 $p$ 一样，$\Phi$ 可以通过微调来学习。尽管它可以基于任何 CNN 块，但为此选择了单个 $3\times 3$ 卷积，然后是空间 softmax 函数，如图 1b 所示。这个单一的卷积减轻了反向传播复杂度的增加。采用 softmax 函数代替 sigmoid 或 ReLU 函数，使得 $\Omega$ 满足 $\Vert \mathbf{\Omega }{\Vert }_1=1$。 公式 2 关于变量 $x$ 和 $\omega$ 以及参数 $p$ 的导数分别由方程 3、4 和 5 给出。在等式的右侧。如图 3 所示，第一项和第二项分别对应于通过图 1b 中的上部和中间路径的反向传播。
$$\begin{array}{rl}\frac{\partial y_k}{\partial x_{i,k}}& =\sum _{j=1}^N\frac{\partial y_k}{\partial {\omega }_j}\frac{\partial {\omega }_j}{\partial x_{i,k}}+{\omega }_i{\left(\frac{x_{i,k}}{y_k}\right)}^{p-1}(3)\\ \frac{\partial y_k}{\partial {\omega }_i}& =\frac{x_{i,k}}{p}{\left(\frac{x_{i,k}}{y_k}\right)}^{p-1}(4)\\ \frac{\partial y_k}{\partial p}& =\frac{y_k}{p}\left(\frac{{\sum }_i{\omega }_i{x}_{i,k}^p\log x_{i,k}}{y_k^p}-\log y_k\right)(5)\end{array}$$
空间加权机制有望反映每个位置激活的判别力。图 2 显示了两个匹配示例。在图 2a 的右图中，wGeM 很好地定位了感兴趣的目标，即 Balliol College，并成功地忽略了遮挡目标，例如树木和房屋。图 2b 显示了一个更具挑战性的示例，其中图像彼此不同，视角和尺度变化很大。

图 2. 由 wGeM 在独立数据集上使用 ResNet101微调生成的匹配图像及其 2D 掩码 $\Omega$。

（补充） Generalized-mean pooling and image descriptor

该文献于2018年发表在TPAMI上

文献地址：链接

添加一个池化层，它以 $\mathcal{X}$ 作为输入并产生一个向量 $\mathbf{f}$ 作为池化过程的输出。该向量在传统全局最大池化的情况下由下式给出
$${\mathbf{f}}^{(m)}={\left[{\mathrm{f}}_1^{(m)}\dots {\mathrm{f}}_k^{(m)}\dots {\mathrm{f}}_K^{(m)}\right]}^{\top },{\mathrm{f}}_k^{(m)}=\underset{x\in {\mathcal{X}}_k}{\max }x(1)$$
而对于平均池化
$${\mathbf{f}}^{(a)}={\left[{\mathrm{f}}_1^{(a)}\dots {\mathrm{f}}_k^{(a)}\dots {\mathrm{f}}_K^{(a)}\right]}^{\top },{\mathrm{f}}_k^{(a)}=\frac{1}{\left|{\mathcal{X}}_k\right|}\sum _{x\in {\mathcal{X}}_k}x.(2)$$
相反，利用广义均值 [55] 并提出使用广义均值 (GeM) 池化，其结果由下式给出
$${\mathbf{f}}^{(g)}={\left[{\mathrm{f}}_1^{(g)}\dots {\mathrm{f}}_k^{(g)}\dots {\mathrm{f}}_K^{(g)}\right]}^{\top },{\mathrm{f}}_k^{(g)}={\left(\frac{1}{\left|{\mathcal{X}}_k\right|}\sum _{x\in {\mathcal{X}}_k}{x}^{p_k}\right)}^{\frac{1}{p_k}}(3)$$
池化方法 (1) 和 (2) 是 (3) 中给出的 GeM 池化的特殊情况，即 $p_k\to \infty$ 时的最大池化和 $p_k=1$ 时的平均池化。特征向量最终由每个特征图的单个值组成，即广义平均激活，其维度等于 $K$。对于许多流行的网络，这等于 256、512 或 2048，使其成为紧凑的图像表示。

池化参数 $p_k$ 可以手动设置或学习，因为此操作是可微的，并且可以是反向传播的一部分。相应的导数（为简洁起见跳过上标 $(g)$）由下式给出
$$\begin{array}{rl}\frac{\partial {\mathrm{f}}_k}{\partial x_i}& =\frac{1}{\left|{\mathcal{X}}_k\right|}{\mathrm{f}}_k^{1-p_k}{x}_i^{p_k-1}\\ \frac{\partial {\mathrm{f}}_k}{\partial p_k}& =\frac{{\mathrm{f}}_k}{p_k^2}\left(\log \frac{\left|{\mathcal{X}}_k\right|}{{\sum }_{x\in {\mathcal{X}}_k}{x}^{p_k}}+p_k\frac{{\sum }_{x\in {\mathcal{X}}_k}{x}^{p_k}\log x}{{\sum }_{x\in {\mathcal{X}}_k}{x}^{p_k}}\right)\end{array}$$
(3) 中的每个特征图都有不同的池化参数，但也可以使用共享的。在这种情况下 $p_k=p,\forall k\in [1,K]$。简单地将其表示为 $p$ 而不是 $p_k$。作者在实验部分检查这些选项，并与手动调整和固定参数值进行比较。

在 MAC 的情况下，最大池化为每个 2D 特征图保留一个激活。这样，每个描述符分量对应一个等于感受野的图像块。然后，通过描述符内积评估成对图像相似度。因此，MAC 相似性隐含地形成了切片对应关系。每个对应的强度由相关描述符组件的乘积给出。在图 2 中，显示了对相似性贡献最大的对应图像块。这种隐式对应关系在微调后得到改善。此外，CNN 在 ImageNet 类上的触发更少，例如汽车和自行车。

图 4 展示了激活的空间分布如何受到广义均值的影响。$p$ 越大，特征图响应就越局部化。最后，在图 3 中，展示了与带有 GeM 池化层（简称 GeM 层）的微调 VGG 匹配的查询和数据库图像的示例。展示了最有助于将该数据库图像与具有很大相似性的非匹配图像区分开来的特征图。

最后一个网络层包括一个 ${\ell }_2$ 归一化层。向量 $\mathbf{f}$ 是 ${\ell }_2$ 归一化的，因此最终使用内积评估两个图像之间的相似性。在本文的其余部分，GeM 向量对应于 ${\ell }_2$ 归一化向量 $\overline{\mathbf{f}}$ 并构成图像描述符。

图 2. 对应于 MAC 描述符维度的图像区域的可视化对成对图像相似度的贡献最大，即描述符素的大乘积。该示例在微调之前（顶部）和之后（底部）使用 VGG。相同的颜色对应于每个图像对的相同描述符组件（特征图）。切片大小等于最后一个局部池化层的感受野。

图 3. 一对查询数据库图像投影在原始图像上的 ${\mathcal{X}}_k^p$ 的可视化。显示的 9 个特征图是数据库图像（右）得分高的特征图，即 GeM 描述符组件的大乘积，但排名靠前的非匹配图像得分低。该示例对所有特征图使用带有 GeM 和单个 $p$ 的微调 VGG，收敛到 2.92。

图 4. 对于三个不同的 $p$ 值，投影在原始图像上的 ${\mathcal{X}}_k^p$ 的可视化。情况 $p=1$ 对应于 SPoC，较大的 $p$ 对应于 (3) 求和之前的 GeM。所示示例使用现成的 VGG。

2.3. Properties of wGeM

如表 1 所示，wGeM 概括了以前的池化方法，例如 sum pooling、weighted sum pooling、max pooling和GeM pooling。与基于均匀池化的GeM 池化不同，wGeM在将图像编码为描述符时忽略了图像的冗余部分。 wGeM也可以应用于区域池化，其中网络产生多个 $\Omega$，每个 $\Omega$ 与单个区域相关联。每个 $\Omega$ 可以直接从每个区域的激活中获得，也可以从从 $\mathbf{X}$ 获得的全局 $\Omega$ 中采样。

表 1. 深度表示的池化方法比较。本文的方法标有 $\star$。使用 wGeM 来表示加权广义均值。

wGeM的一个重要特性与其在 $p\to \infty$ 时的行为有关。在这种情况下，公式 2 退化到最大池化，而与 $\omega$ 无关。在反向传播期间，损失 $\mathcal{L}$ 对 $\omega$ 的导数为
$$\frac{\partial \mathcal{L}}{\partial {\omega }_i}=\frac{1}{p}\sum _{k=1}^K\frac{\partial \mathcal{L}}{\partial y_k}{\left(\frac{x_{i,k}}{y_k}\right)}^{p-1}{x}_{i,k}(6)$$
其中 ( x i , k y k ) p − 1 ∈ { 0 , 1 } \left(\frac{x_{i, k}}{y_{k}}\right)^{p-1} \in\{0,1\} (yk​xi,k​​)p−1∈{
0,1} 并且仅当 $y_k=x_{i,k}$ 时才等于1。因此，当 $\frac{1}{p}\to 0$ 时，公式 6 接近零。也就是说，所有 ${\omega }_i\in \Omega$ 在前向和后向传播期间都变得无效。$\mathcal{L}$ 关于 $p$ 的导数也存在类似的问题。在实践中，学习到的 $p$ 在本文的实验中从未达到很大的值，这与GeM pooling的结果一致。

参考文献

[6] Filip Radenovic, Giorgos Tolias, and Ondrej Chum, “Finetuning CNN image retrieval with no human annotation,” CoRR, 2017. 1, 2, 3, 4

[55] P . Dollár, Z. Tu, P . Perona, and S. Belongie, “Integral channel features.” in BMVC, 2009. 4