C++ 漫谈哈夫曼树
欢迎光临:编程驿站，更多好文等你来！
1. 前言
什么是哈夫曼树？
把权值不同的个结点构造成一棵二叉树，如果此树满足以下几个条件：此 个结点为二叉树的 。较大的结点离根结点较近，权值较小的结点离根结点较远。该树的是所有可能构建的二叉树中最小的。
则称符合上述条件的二叉树为最优二叉树，也称为。
构建哈夫曼树的目的是什么？
用来解决在通信系统中如何使用最少的二进制位编码字符信息。
本文将和大家聊聊哈夫曼树的设计思想以及构建过程。
2. 设计思路
产生的背景：
在通信系统中传递一串文本时，对这一串字符串文本进行二进制编码时，如何保证所用到的位是最少的，或保证整个编码后的传输长度最短。
现假设字符串由个字符组成，最直接的思维是使用 个位进行，如下表格所示：字符编码A00B01C10D11
传输字符串一次时，所需为 位，当通信次数达到 次时，则需要的总传输长度为 。当字符串的传输次数为 次时，所需要传输的总长度为 个。
使用时，如果传输的报文中有 个不同字符时，因需要对每一个字符进行编码，至少需要 位。
但在实际应用中，各个字符的出现频率或使用次数是不相同的，如的使用频率远远高于。使用等长编码特点是无论字符出现的频率差异有多大，每一个字符都得使用相同的位。
哈夫曼的设计思想是：对字符串信息进行编码设计时，让使用频率高的字符使用，使用频率低的用，以优化整个信息编码的长度。基于这种简单、朴素的想法设计出来的编码也称为。
哈夫曼不等长编码的具体思路如下：
如现在要发送仅由 个字符组成的报文信息 ，字符在信息中占比为 ，的占比是 ，的占比是 ， 的 占比是。
不等长编码的朴实思想是的占比越大，所用的位就少，占比越小，所用位越多。如下为每一个字符使用的位数：使用 位编码。使用 位 编码。 使用 位 编码。 使用 位 编码。
具体编码如下表格所示：字符占比编码A0.50B0.210C0.15110D0.1111
如此编码后，是否真的比前面的等长编码所使用的总位要少？
计算公式=。 先计算每一个字符在报文信息中的占比乘以字符所使用的位。 然后对上述每一个字符计算后的结果进行相加。
显然，编码只需要 个 ，比等长编码用到的位要少 。当传输信息量为 时，总共所需要的位=。
为什么称哈夫曼编码为哈夫曼树?
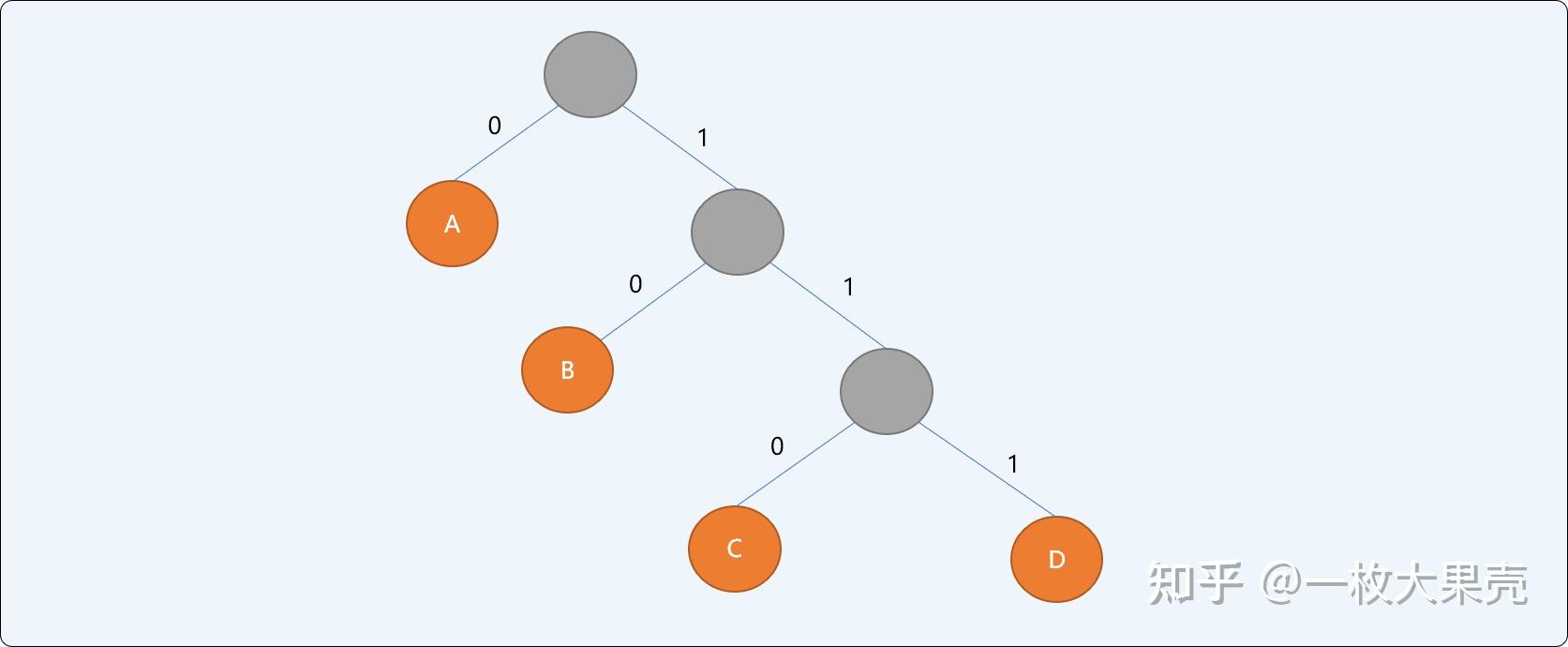
因为字符的编码是通过构建一棵的二叉树推导出来的，如下图所示：
哈夫曼树的特点：信息结点都是叶子结点。叶子结点具有权值。如上二叉树，结点权值为，结点权值为，结点权值为，结点权值为 。哈夫曼编码为不等长前缀编码（即要求一个字符的编码不能是另一个字符编码的前缀）。从开始，为左右分支分别编号和，然后顺序连接从根结点到叶结点所有分支上的编号得到字符的编码。
相信大家对哈夫曼树有了一个大概了解，至于如何通过构建哈夫曼树，咱们继续再聊。
3. 构建思路
在构建之前，先了解几个相关概念：路径和路径长度：在一棵树中，从一个结点往下可以达到的孩子或孙子结点之间的通路，称为。通路中分支的数目称为。若规定根结点的层数为，则从根结点到第层结点的路径长度为。 结点的权及带权路径长度：若将树中结点赋给一个有着某种含义的数值，则这个数值称为该结点的。结点的带权路径长度为：从根结点到该结点之间的路径长度与该结点的权的乘积。 树的带权路径长度：树的带权路径长度规定为所有叶子结点的带权路径长度之和，记为。
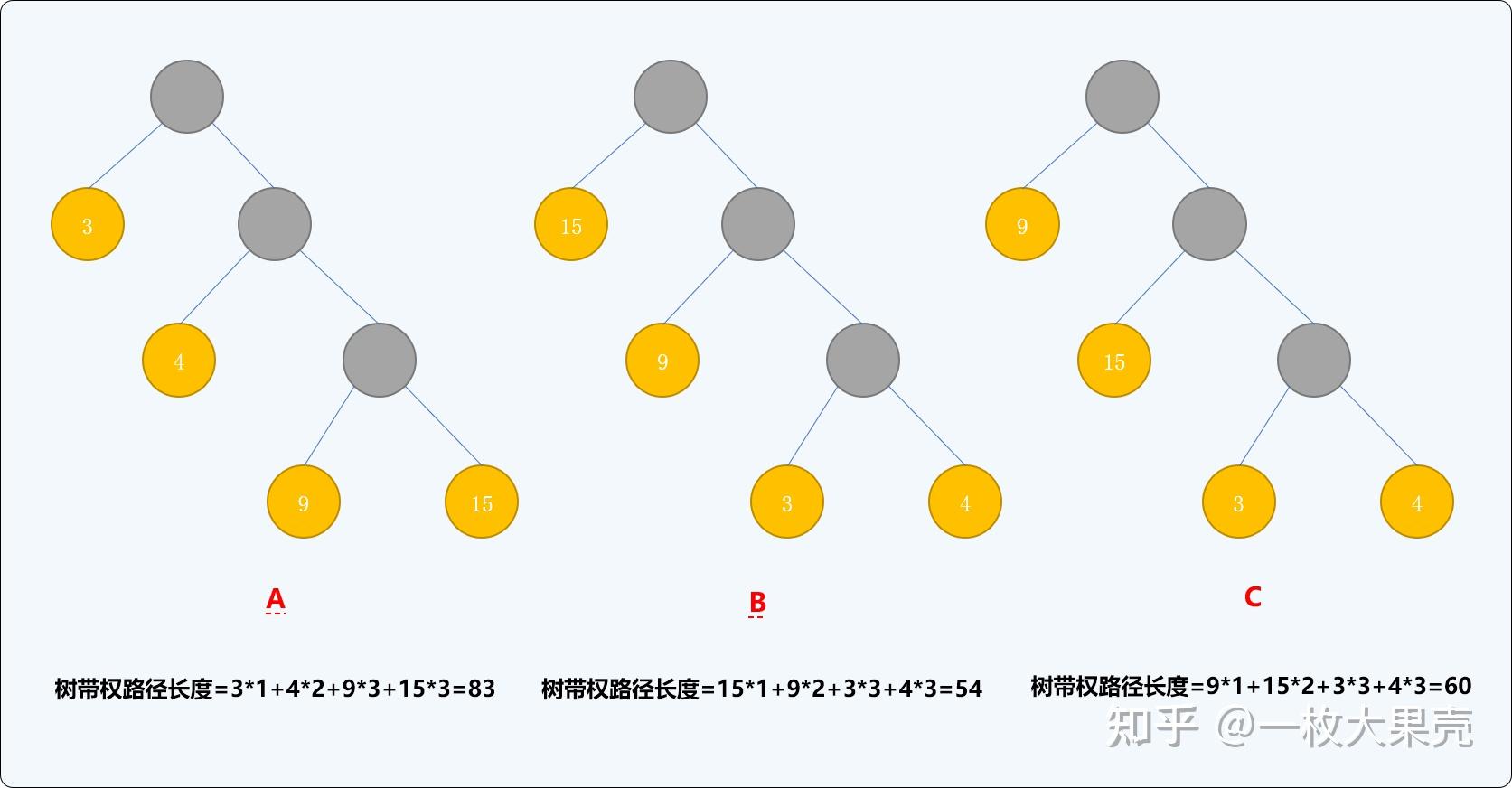
如有权值为的 个结点，则可构造出不同的二叉树，其带权路径长度也会不同。如下 种二叉树中，的树带权路径长度是最小的。
的构建过程就是要保证最小。
那么，如何构建二叉树，才能保证构建出来的二叉树的带权路径长度最小？
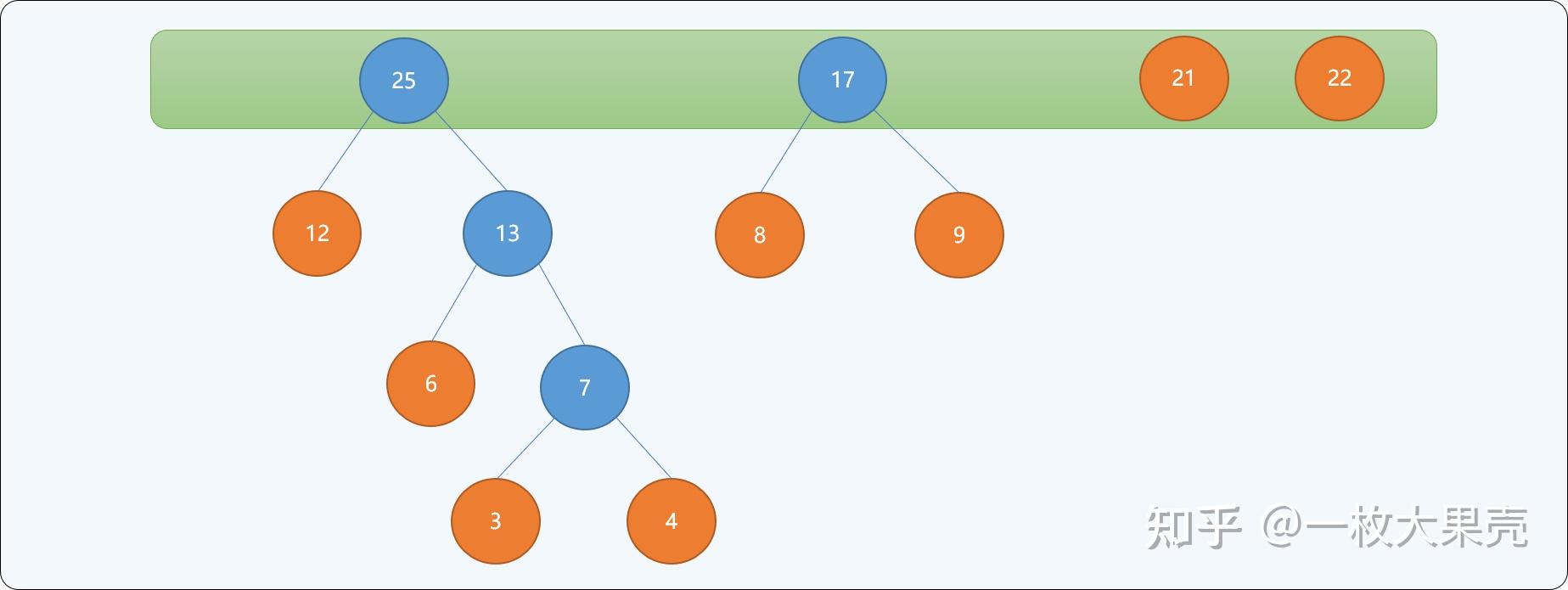
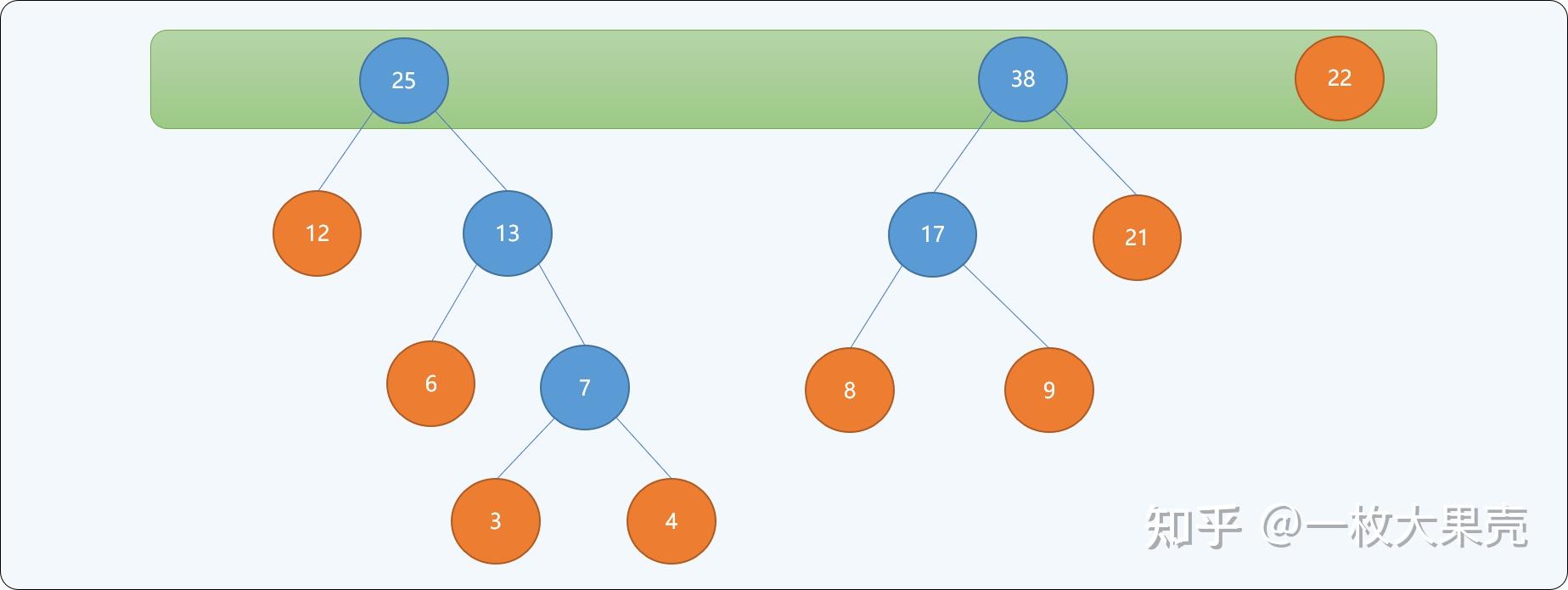
如有一信息由 个字符组成，每一个字符的分别为，构建最优哈夫曼树的流程：以每一个结点为根结点构建一个单根二叉树，二叉树的左右子结点为空，根结点的权值为每个结点的权值。并存储到一个树集合中。
从中选择根结点的权值最小的 个树。重新构建一棵新二叉树，让刚选择出来的 颗树的根结点成为这棵新树的左右子结点，新树的根结点的权值为 个左右子结点权值的和。构建完成后从树集合中删除原来 个结点，并把新二叉树放入树集合中。 如下图所示。权值为 和的结点为新二叉树的左右子结点，新树根结点的权值为。 
重复第二步，至到树集合中只有一个根结点为止。
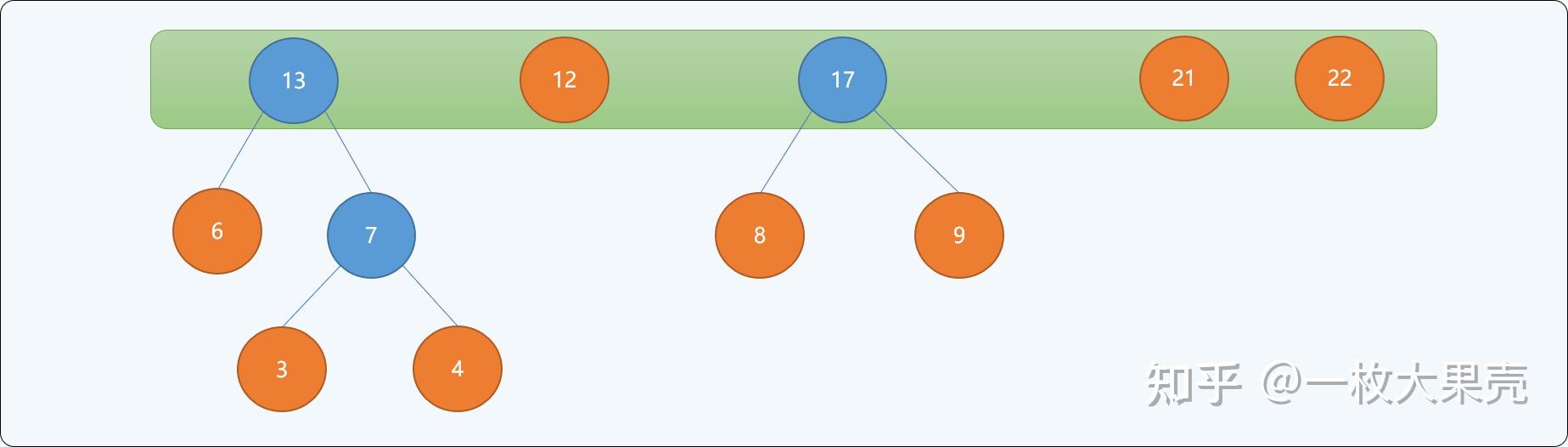
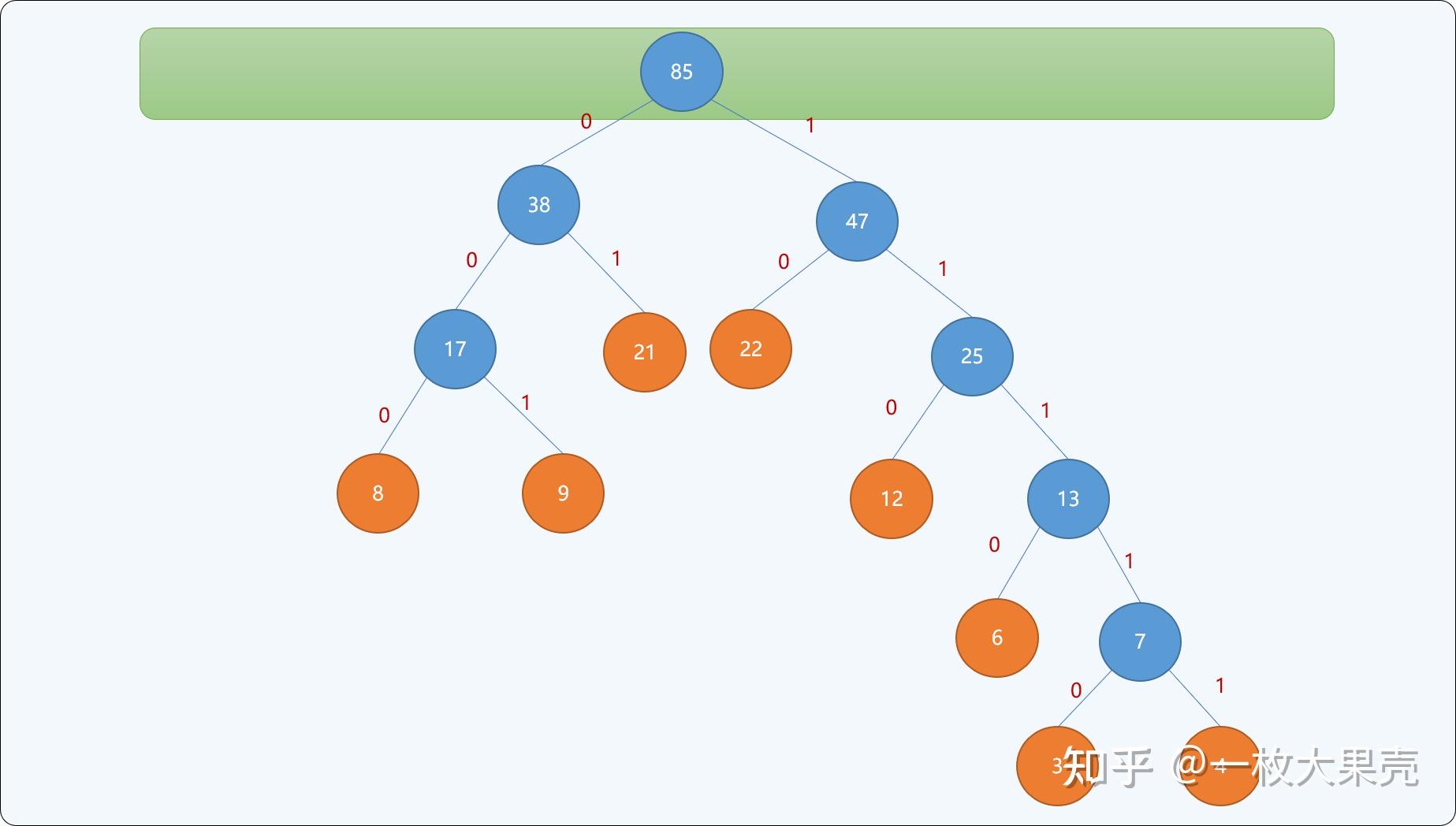
当最后集合中只存在一个根结点时，停止构建，并且为最后生成树的每一个非叶子结点的左结点分支标注，右结点分支标注。如下图所示：
通过上述从下向上的思想构建出来的二叉树，可以保证权值较小的结点离根结点较远，权值较大的结点离根结点较近。最终二叉树的带权路径长度： 。并且此树的带权路径长度是所有可能构建出来的二叉树中最小的。
上述的构建思想即为哈夫曼树设计思想，不同权值的字符编码就是结点路径上和的顺序组合。如下表所述，权值越大，其编码越小，权值越小，其编码越大。其编码长度即从根结点到此叶结点的路径长度。字符权值编码A311110B61110C12110D9001E411111F8000G2101H2210
4. 编码实现
4.1 使用优先队列
可以把不同的结点分别存储在中，并且给与权重较低的结点较高的。
具体实现哈夫曼树算法如下：把个结点存储到优先队列中，则个节点都有一个优先权。这里是权值越小，优先权越高。如果队列内的节点数>1，则：从队列中移除两个最小的结点。 产生一个新节点，此节点为队列中移除节点的父节点，且此节点的权重值为两节点之权值之和，把新结点加入队列中。 重复上述过程，最后留在优先队列里的结点为哈夫曼树的根节点（）。
完整代码：
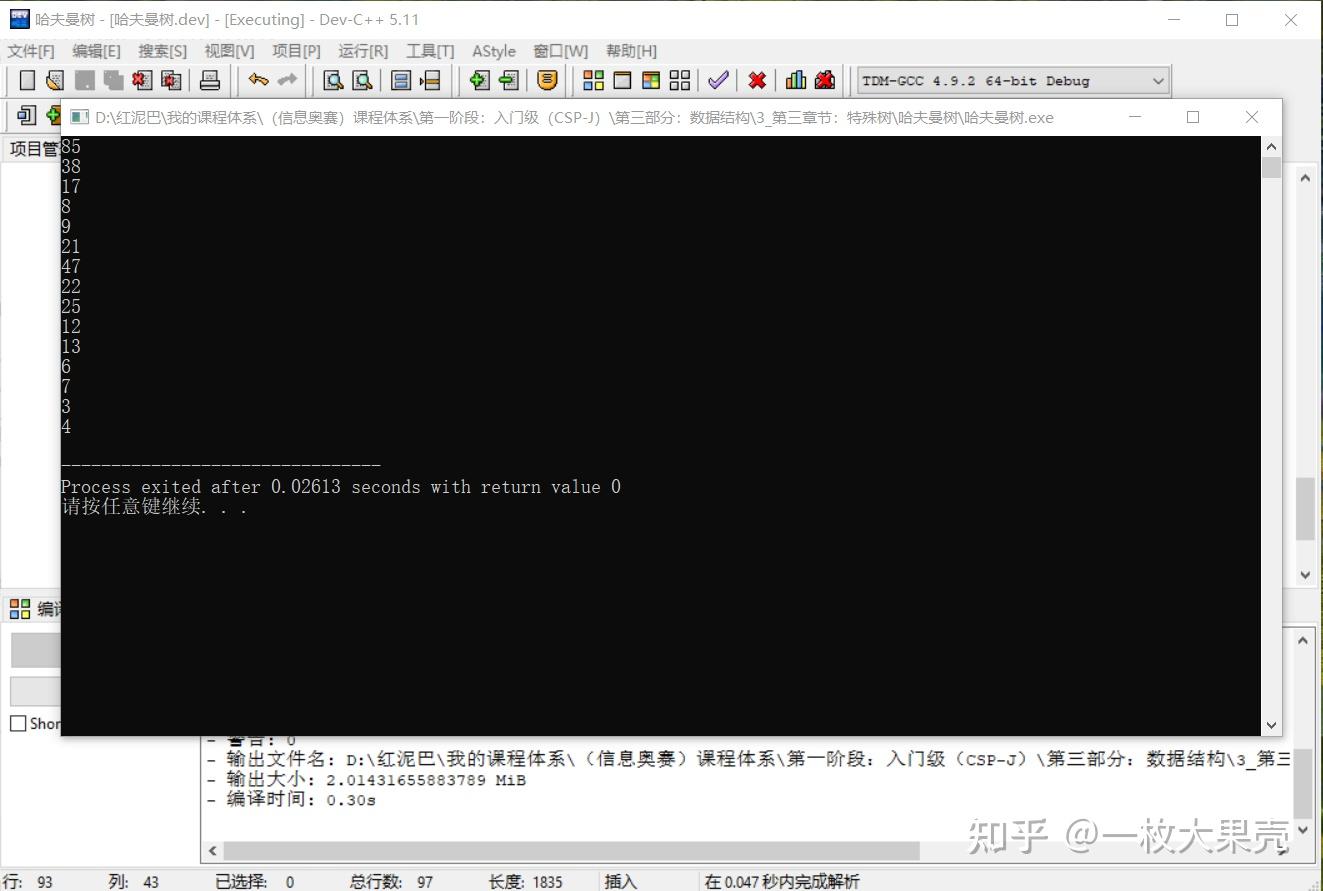
显示结果：
上述输出结果，和前文的演示结果是一样的。
此算法的时间复杂度为。因为有个结点，所以树总共有个节点，使用优先队列每个循环须。
4.2 使用一维数组
除了上文的使用优先队列之外，还可以使用一维数组的存储方式实现。
在哈夫曼树中，叶子结点有 个，非叶子结点有 个，使用数组保存哈夫曼树上所的结点需要 个存储空间 。其算法思路和前文使用队列的思路差不多。直接上代码：
测试结果：
5. 总结
哈夫曼树是二叉树的应用之一，掌握哈夫曼树的建立和编码方法对解决实际问题有很大帮助。
2024最新激活全家桶教程，稳定运行到2099年，请移步至置顶文章：https://sigusoft.com/99576.html
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请联系我们举报，一经查实，本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处：https://sigusoft.com/96404.html
![PyCharm激活2023.2.4([Python急救站课程]Python集成环境IDEA：Pycham专业版2023.2.3安装与激活成功教程方法)](https://sigusoft.com/wp-content/uploads/2024/06/aYly8PH-480x300.png "PyCharm激活2023.2.4([Python急救站课程]Python集成环境IDEA：Pycham专业版2023.2.3安装与激活成功教程方法)缩略图")
