第3章-正弦交流电路-3.4电阻、电感、电容元件的正弦交流电路
3.4电阻、电感、电容元件的正弦交流电路
电工学_中国大学MOOC(慕课)
知识点概述:
(第4讲 电阻、电感、电容元件的正弦交流电路)
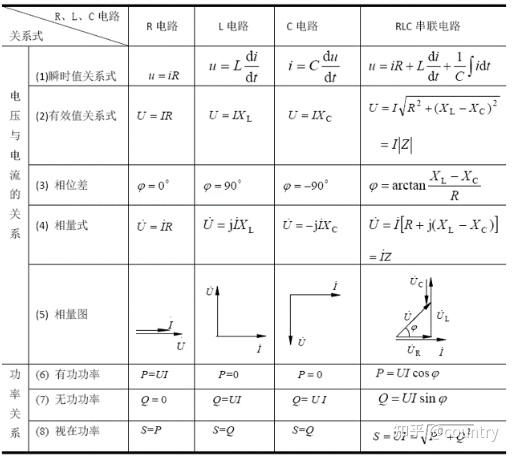
4.1电阻元件的正弦交流电路
1、在电阻元件的两端施加正弦交流电压 





设正弦电压初始相位为0,则 
则
(其中 


观察后可发现,
(1)电压 

(2)大小关系: 

(3)相位关系:相位差 


(4)相量式如下,称为电阻元件欧姆定律的向量形式。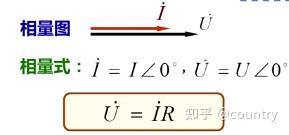
2、电阻元件正弦交流电路中的功率与能量的转换:
因为前面推导出,在正弦交流电路中,电压 

(1)瞬时功率 
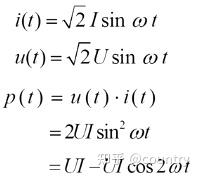
即 

电阻元件的瞬时功率是一个恒定量( 

结论:瞬时功率 
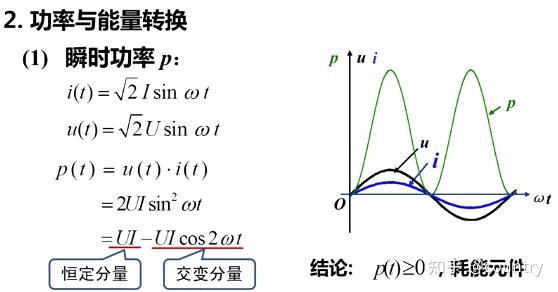
(2)为了说明电路实际消耗的功率,我们引入平均功率(有功功率) 
去一个周期的时间 




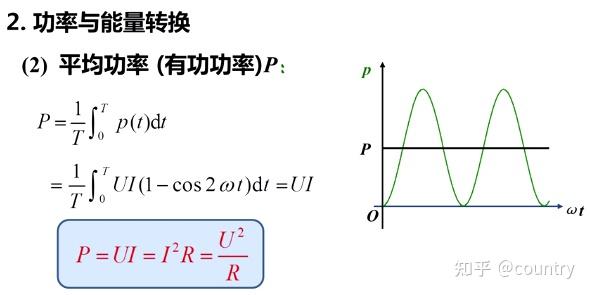
3、电阻元件无功功率
说明:理想电阻元件与电源之间没有能量交换。即从电源的全部能量,都转换为热能消耗掉了。
4.2电感元件的正弦交流电路
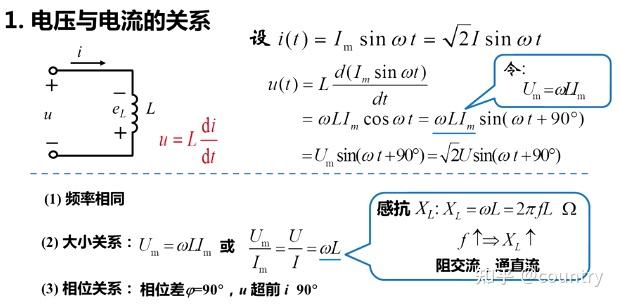
1、在电感元件上输入电流 




设 
微分后可得
令 
比较后可发现:
(1)电压 

(2)大小关系: 

电压与电流的比值具有与电阻相同的量纲,定义 

由 


频率 

因此电感有通直流,阻交流的特性。
(3)电感电路,电流与电压的相位差 
如果用相量表示电压与电流的关系,即电感元件欧姆定律的复数形式,由于 
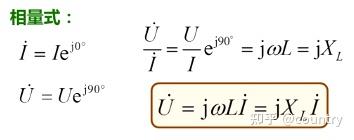
其中, 
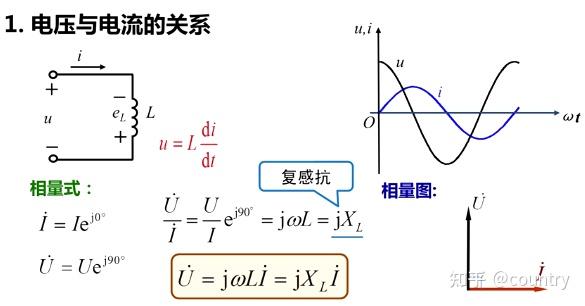
2、电感元件正弦交流电路中的功率与能量的转换:
设电感上流过的电流的初相位为0,有前面的分析可知,电感两端的电压超前于电流90°,
(1)瞬时功率 
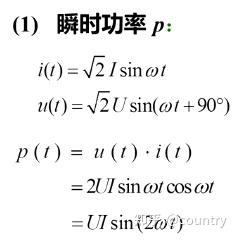
即 

瞬时功率是幅值为 
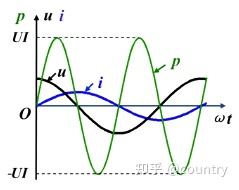
结论:瞬时值有时为正,有时为负,表明电感时而吸收能量,时而放出能量,与电源之间存在能量交换。故电感是储能元件。
(2)电感元件实际消耗的功率,即平均功率(有功功率) 

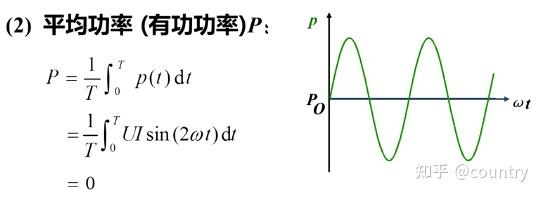
结论:理想的电感是非耗能元件。
(3)无功功率 
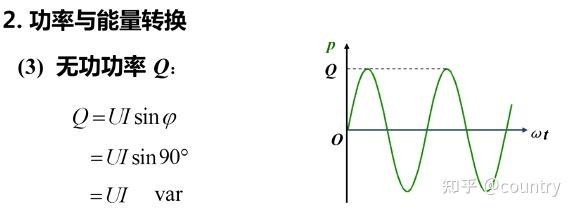
即
结论:理想电感元件从电源吸收的功率全部用来交换。
4.3电容元件的正弦交流电路
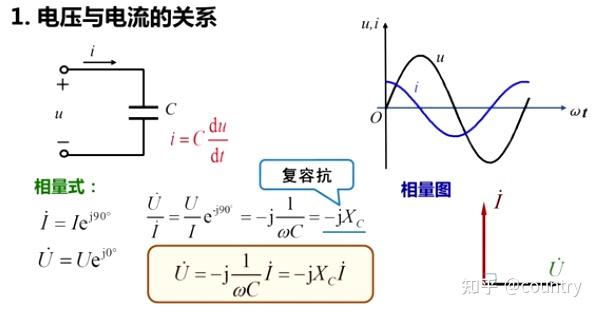
1、电容元件两端施加正弦交流电压 




设 

则电流
令
则
比较后发现:
(1)电压 

(2)大小关系: 

其中 

由 




(3)电容电路,电流与电压的相位差 
如果用相量表示电压与电流的关系,即电容元件欧姆定律的复数形式: 
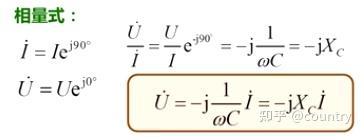
其中, 
2、电容元件正弦交流电路中的功率与能量的转换:
设电感上流过的电流 
(1)瞬时功率 

即 

瞬时功率 

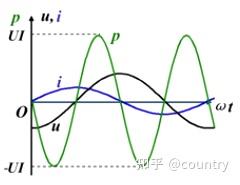
结论:瞬时值有时为正,有时为负,表明电容元件时而吸收能量,时而放出能量,与电源之间存在能量交换。故电容是储能元件。
注意:式中的负号是为了与电感元件相比较,在同一个电流的作用下,电容和电感的瞬时功率的极性是完全相反的,即一个在吸收能量,另一个在释放能量。
(2)电容元件实际消耗的功率,即平均功率(有功功率) 

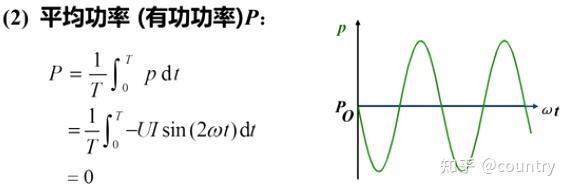
结论:理想的电容是非耗能元件。
(3)无功功率 
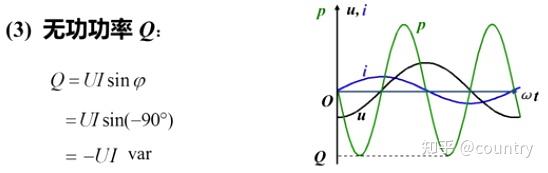
即
结论:理想电容元件从电源吸收的功率全部用来交换。
注意:电容元件无功功率 



2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/96324.html