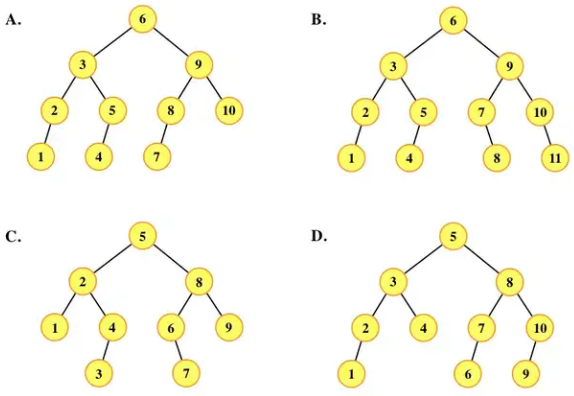
下列二叉树中,可能成为折半查找判定树(不含外部结点)的是()
折半查找判定树实际上是一棵二叉搜索树,它的中序遍历序列是一个单调序列。
折半查找即二分查找,假设搜索的有序数组为 A[1:n] ,目标元素为 target,二分查找伪代码如下:
向下取整:
向上取整:
方法一:构造
A选项二叉树10个结点。
B选项二叉树11个结点。
C选项二叉树9个结点。
D选项二叉树10个结点。
我们尝试构造一棵含10个元素的折半查找判定树,每个结点存储数组元素下标。
设有长度为10的升序序列 A[1:10] ,即满足 a1<a2<a3<a4<a5<a6<a7<a8<a9<a10 。为了方便讨论,考虑下标序列 {1,2,3,4,5,6,7,8,9,10} 。
折半查找规则要统一,要不全部折半向下取整,要不全部折半向上取整。下面分情况讨论。
折半向下取整:
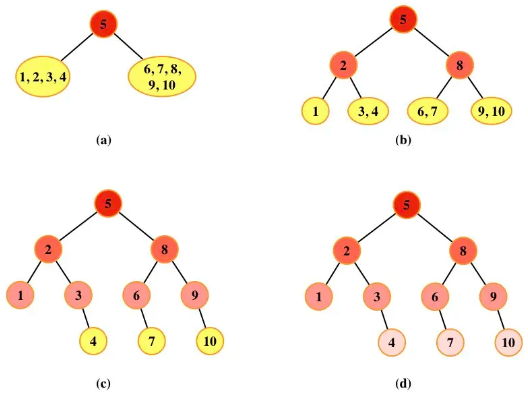
根结点元素下标为⌊(1 + 10) / 2⌋ = 5,下标序列 {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}分为{1, 2, 3, 4}, {5}, {6, 7, 8, 9, 10}。对于左子树,根结点元素下标为⌊(1 + 4) / 2⌋ = 2。{1, 2, 3, 4}可以分为{1}, {2}, {3, 4}。对于右子树,根结点元素下标为⌊(6 + 10) / 2⌋ = 8。{6, 7, 8, 9, 10}可以分为{6, 7}, {8}, {9, 10}。递归执行上述过程直到折半查找判定树构造完成。
折半向上取整:
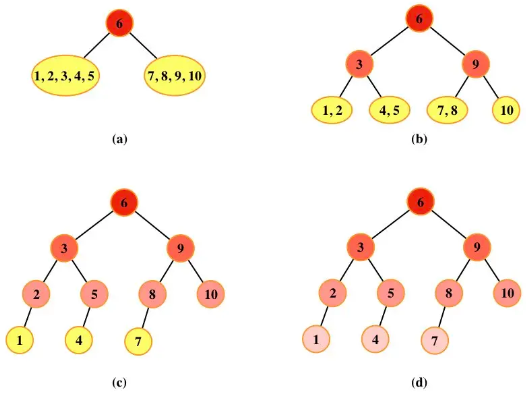
根结点元素下标为⌈(1 + 10) / 2⌉ = 6,下标序列{1, 2, 3, 4, 5, 6, 7, 8, 9, 10}分为{1, 2, 3, 4, 5}, {6}, {7, 8, 9, 10}。对于左子树,根结点元素下标为⌈(1 + 5) / 2⌉ = 3。{1, 2, 3, 4, 5}可以分为{1, 2}, {3}, {4, 5}。对于右子树,根结点元素下标为⌈(7 + 10) / 2⌉ = 9。{7, 8, 9, 10}可以分为{7, 8}, {9}, {10}。递归执行上述过程直到折半查找判定树构造完成。
此折半查找判定树与选项A中的二叉树一致。
本题选A。
方法二:代入选项
考虑升序序列 A[1:n] ,其中 n 为对应二叉搜索树的结点个数,可以在树结点上依次填上相应的元素下标,符合折半查找规则的二叉树树即为所求。
折半查找规则要统一,要不全部折半向下取整,要不全部折半向上取整。
B选项中,观察以元素下标 2 为根结点的子树,二分查找区间为 [1, 2],⌈(1 + 2) / 2⌉ = 2;观察以元素下标 7 为根结点的子树,二分查找区间为 [7, 8],⌊(7 + 8) / 2⌋ = 7,错误。
C选项,观察以元素下标 2 为根结点的子树,二分查找区间为 [1, 4],⌊(1 + 4) / 2⌋ = 2;观察以元素下标 8 为根结点的子树,二分查找区间为 [6, 9],⌈(6 + 9) / 2⌉ = 8,错误。
D选项,观察以元素下标 7 为根结点的子树,二分查找区间为 [6, 7],⌈(6 + 7) / 2⌉ = 7;观察以元素下标 5 为根结点的子树,二分查找区间为 [1, 10],⌊(1 + 10) / 2⌋ = 5,错误。
只有A选项符合折半查找规则,正确。
本题选A。
方法三:确定性
本题考察算法的确定性。
折半查找规则要统一,要不全部折半向下取整,要不全部折半向上取整。也就是只有一个孩子结点的子树孩子结点固定在一侧,可以断言:下面两个命题必然有一个为真。
对于任意一个结点,其左子树结点个数大于或等于其右子树结点个数。
对于任意一个结点,其左子树结点个数小于或等于其右子树结点个数。
命题1对应折半向上取整的情况,命题2对应折半向下取整的情况。
观察最下面一层子树,只有选项A和D符合要求,均满足命题1,继续扩大范围观察,观察根结点所在子树,即整棵树,发现D中出现了右子树结点比左子树结点多的情况,违反命题1,排除。只有A符合要求。
本题选A。
2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/96230.html