一文搞懂如何构造哈夫曼树?
上文介绍了哈夫曼树的基本概念:机器学习入坑者:程序员必备——哈夫曼树的基本概念
哈夫曼树要求所有叶子节点的带权路径最小,那么如何构造这样的树呢?
图说构造方式
首先,对将要使用的符号进行定义:节点数目为n;n个节点对应的权值为{w1,w2,…wn};n个节点构成的集合为T={T1,T2,…Tn};
其中,“n个节点”表示n个叶子节点,也表示根节点,这n个节点都没有左右子树。
构造的针对的是什么?
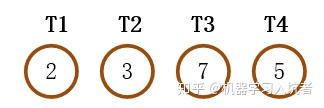
哈夫曼树的构造是针对带权的叶子节点进行的,下图的数字表示节点的权值:
构造哈夫曼树的步骤
(1)选择与合并
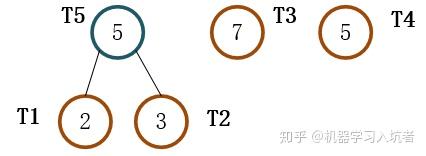
从集合T中选择权值最小的两个节点,即2和3。使用权值最小的两个节点作为左右子树(图中的T1和T2),构造新的树T5,新的树的权值为左右子树权值之和:
需要注意的是,使用权值最小的两个节点构建新的树时,应该将权值较小的节点T1作为左子树,权值较大的节点T2作为右子树。(如果T1和T2的权值相同,则将深度较小的作为左子树)
(2)增加与删除
从集合T中删除权值最小的两个节点(即T1和T2),然后将新创建的节点加入集合T(即T5)。此时,集合T={T3, T4, T5}。
经过一次合并以后,集合T的节点数目减一。减少两个节点,新增一个节点。
(3)重复操作
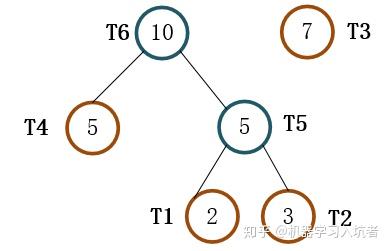
不断的重复上述两个步骤,直到集合T只剩下一个元素为止,即最后哈夫曼树的根节点。下面是第二次操作后的节点情况:
在第二次合并操作时,集合T删除了权值最小的两个节点(T4和T5),增加了节点T6(T6的权值为T4和T5的权值之和)。此时,集合T元素数目再次减一,T={T3, T6}。
接下来,是第三次合并操作后的节点情况:
在第三次合并以后,集合T仅剩一个元素T7,权值为17。此节点即为哈夫曼树的根节点。
总结:
构建哈夫曼树时,各个步骤涉及到了几个非常重要的概念:寻找集合T中权值最小的两个节点;使用两个权值最小的节点构建新的节点;
下一篇笔记将会记录哈夫曼树的代码实现,并给出实例进行分析。
2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/96028.html