哈夫曼树带权路径长度(WPL)计算
概念
路径：在一棵树中，从一个结点到另一个结点所经过的所有结点，被我们称为两个结点之间的路径路径长度：在一棵树中，从一个结点到另一个结点所经过的“边”的数量，被我们称为两个结点之间的路径长度。 结点的带权路径长度：树的根结点到该结点的路径长度和该结点权重的乘积 树的带权路径长度：在一棵树中，所有叶子结点的带权路径长度之和，被称为树的带权路径长度，也被简称为WPL。
计算方法
问题描述：给定树T，有n个叶结点，并且其权重值为{A1,A2,A3…An};如何计算树T的WPL
例如2021年408这道题
方法1
按照算法步骤画出哈夫曼树
具体算法如下：
举例说明首先对集合进行排序得到 我们找到权值最小的两个结点10和12合并；得到新的森林根结点为22。现在结点集合为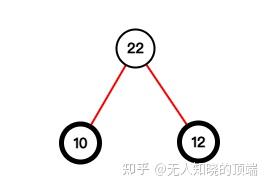 
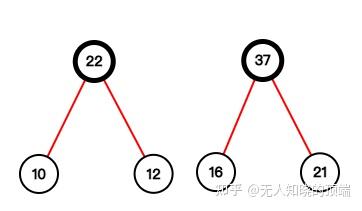
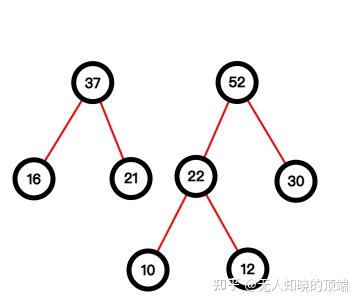
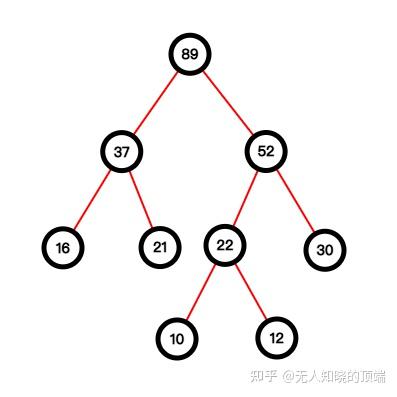
接着我们找到当前最小的结点16和21合并：得到新的森林根结点为37。现在结点集合为 
接着我们找到当前最小的结点22和30合并：得到新的森林根结点为53。现在结点集合为 
接着我们找到当前最小的结点37和53合并：得到新的森林根结点为90。现在结点集合为；由于结点个数只剩一个，所以算法结束、构造哈夫曼树完毕
可以看到哈夫曼树的构造堆左右子树的顺序是没有要求的，当然我们画哈夫曼树的可以按照一定规律来这样更明确思路更清晰，比如我这里是按照的原则来画的
2. 依次累加计算所有叶结点的带权路径长度
从上面构造的哈夫曼树可知所有结点的路径长度，例如结点”16“的路径长度为2。所以
方法2
按照算法步骤画出哈夫曼树：步骤同方法1将所有非根结点的权值累加起来：WPL=37+53+16+21+22+30+10+12=200
这里我简单证明下上述结论：1. 对于哈夫曼树T1中的两个兄弟叶结点N1、N2，假设N1、N2的父结点为P1、N1的路径长度为d
2. 删除结点N1、N2得到的哈夫曼树为T2
因为得到 所以；按照哈夫曼树构造过程，可知，即WPL为所有叶结点的权值之和
方法3
不画哈夫曼树直接计算WPL 按照方法2的过程，我们可以每次找到最小两个结点后，直接累加到WPL里递归计算WPL 即过程如下：首先对集合进行排序得到 一开始去掉最小的两个结点得到，去掉最小的两个结点得到，去掉最小的两个结点得到，只剩两个结点了，直接累加，
代码实现
JS实现
C语言实现
2024最新激活全家桶教程，稳定运行到2099年，请移步至置顶文章：https://sigusoft.com/99576.html
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请联系我们举报，一经查实，本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处：https://sigusoft.com/95985.html
