哈夫曼编码如何做? 这个题怎么做啊，为啥我做出来这么奇怪呢。拜托告诉孩子哪里错了，拜托大佬救救我啊，有偿也可以啊
简单介绍一下哈夫曼树、哈弗曼编码： 从树中一个结点到另一个结点之间的分支构成两个结点之间的路径，路径上的分支数目称做路径长度。 树的路径长度就是从树根到每一结点的路径长度之和。 如果考虑到带权的结点，结点的带权的路径长度为从该结点到树根之间的路径长度。与结点上权的乘积。树的带权路径长度为树中所有叶子结点的带权路径长度之和。 带权路径长度WPL最小的二叉树称做哈夫曼树[1]
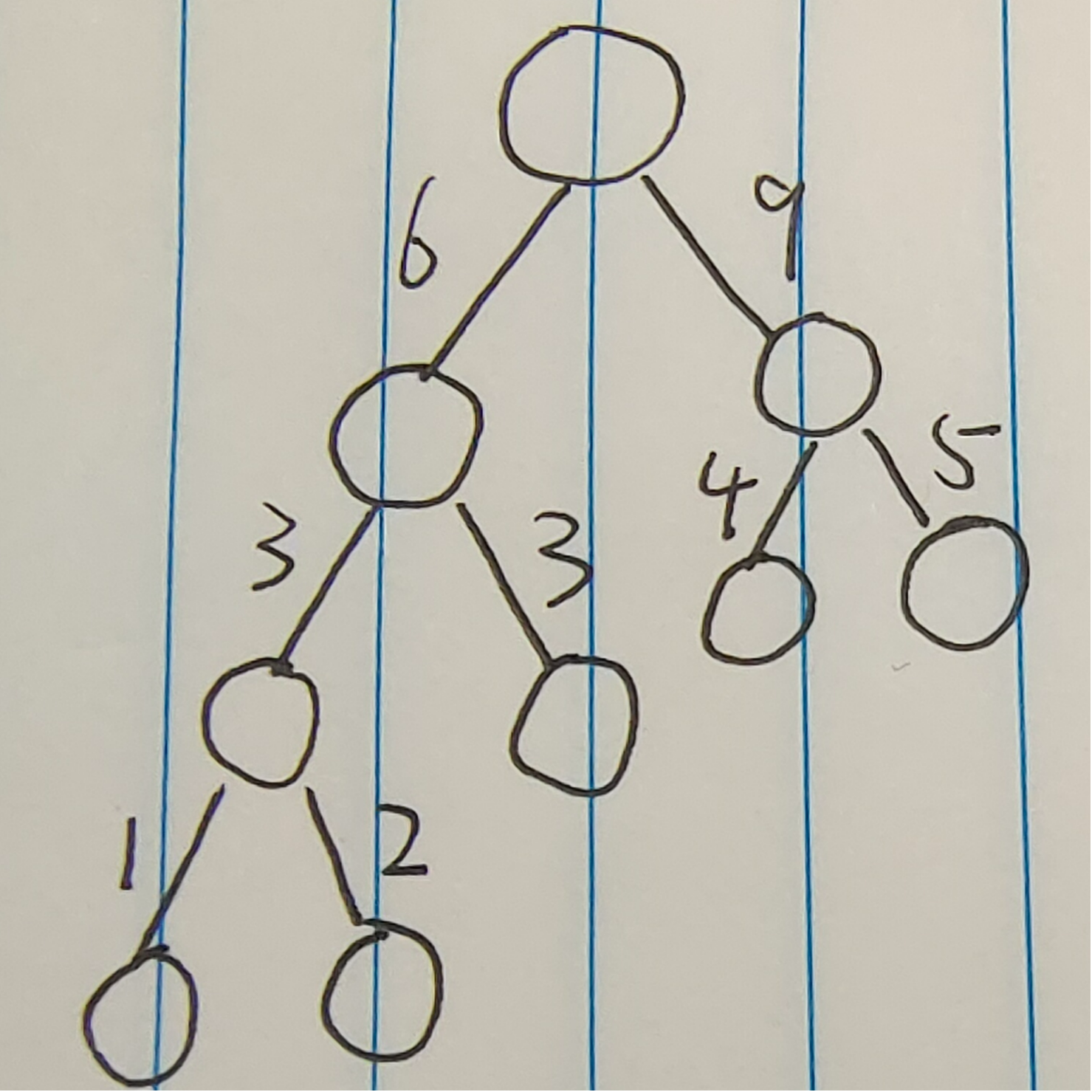
哈夫曼编码 哈夫曼树不一定是二叉树。 习题： 1.用5个权值{3, 2, 4, 5, 1}构造的哈夫曼（Huffman）树的带权路径长度是（ ） 解析：33；先构造哈夫曼树，得到各叶子的路径长度之后便可求出WPL。
题1哈夫曼树 2. 具有10个叶子结点的哈夫曼树，最大高度为（ ），最小高度为（ ）。 解析：10,5； n个叶子结点的哈夫曼树，最大高度为n，(除最上一层和最下一层每层一个叶子点)，最小高度为log2 n +1 3. 根据使用频率为5的字符设计的哈夫曼编码不可能是（ ） A．111，110，10，01，00 B、000，001，010，011，1 C．100，11，10，1，0 D、001，000，01，11，10 解析：选C；C中，100和10冲突（单独存在1、0和其它的也冲突），即一个结点既是叶子结点又是内部结点，哈夫曼树中不可能出现这种情况。 一个树可以看做由三种结点组成：根结点（唯一）、内部结点、叶结点
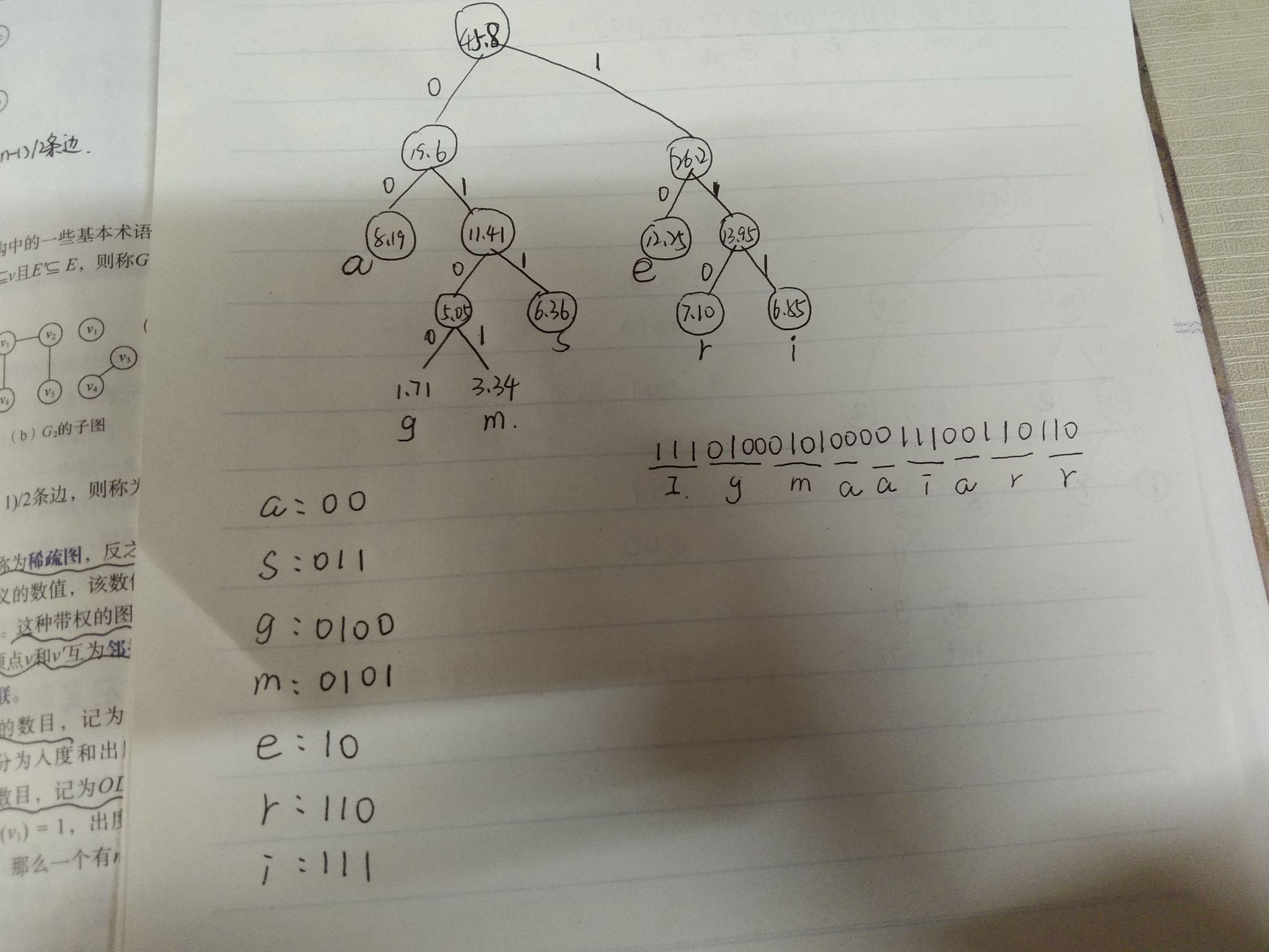
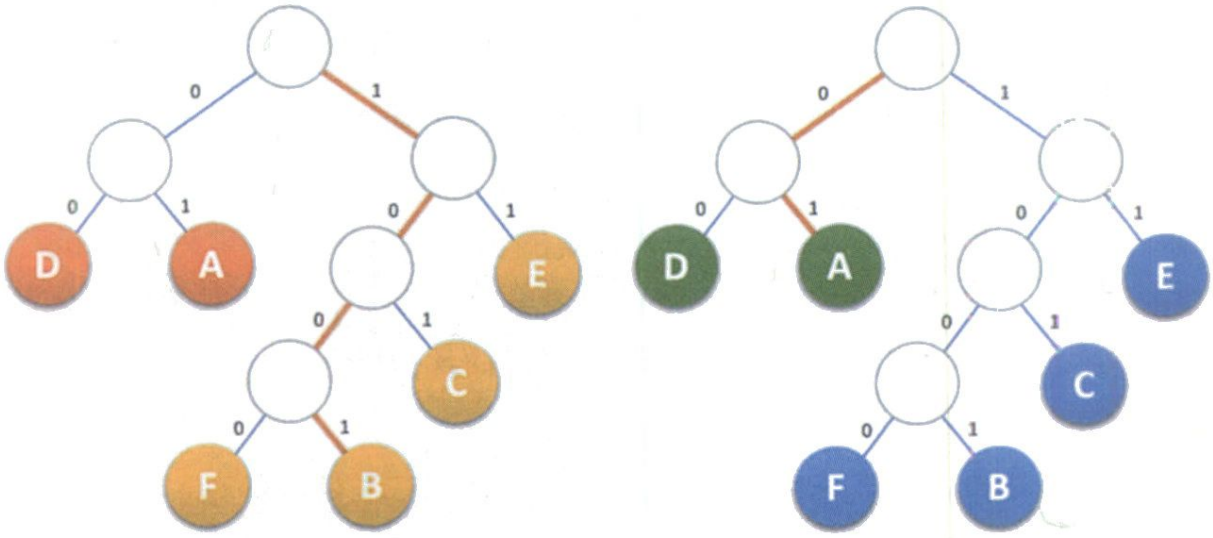
4. 根据使用频率为5的字符设计的哈夫曼编码不可能是（ ） A、000，001，010，011，1 B、0000，0001，001，01，1 C．000，001，01，10，11 D、00，100，101，110，111 解析：选D； 哈夫曼树的结点只能是0度或2度。 哈夫曼树的结点只能是0度或2度。 哈夫曼树的结点只能是0度或2度。 按照D的画法，00对应的父结点的度为1度，因为不存在01；该题规定了频率为5的字符设计，另外4叶结点已经被占用，所以只有00没有01，不符合哈夫曼编码的规定。 5. 假设用于通信的电文仅由8个字母组成，字母在电文中出现的频率分别为0.07，0.19，0.02，0.06，0.32，0.03，0.21，0.10。试为这8个字母设计哈夫曼编码。使用0～7的二进制表示形式是另一种编码方案。对于上述实例，比较两种方案的优缺点。 解析：方案一：哈夫曼编码 先将概率放大100倍，以方便构造哈夫曼树。w={7,19,2,6,32,3,21,10} 注意：哈夫曼树是不唯一的！哈夫曼树是不唯一的！哈夫曼树是不唯一的！因为没有限定左右子树,并且有权值重复时,可能树的高度都不唯一,唯一的只是带权路径长度之和最小。 方案1的WPL＝2(0.19+0.32+0.21)+4(0.07+0.06+0.10)+5(0.02+0.03)=1.44+0.92+0.25=2.61 方案2的WPL＝3(0.19+0.32+0.21+0.07+0.06+0.10+0.02+0.03)=3 结论：哈夫曼编码优于等长二进制编码
2024最新激活全家桶教程，稳定运行到2099年，请移步至置顶文章：https://sigusoft.com/99576.html
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请联系我们举报，一经查实，本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处：https://sigusoft.com/90020.html
