二叉排序树非递归遍历讲解_二叉树的定义

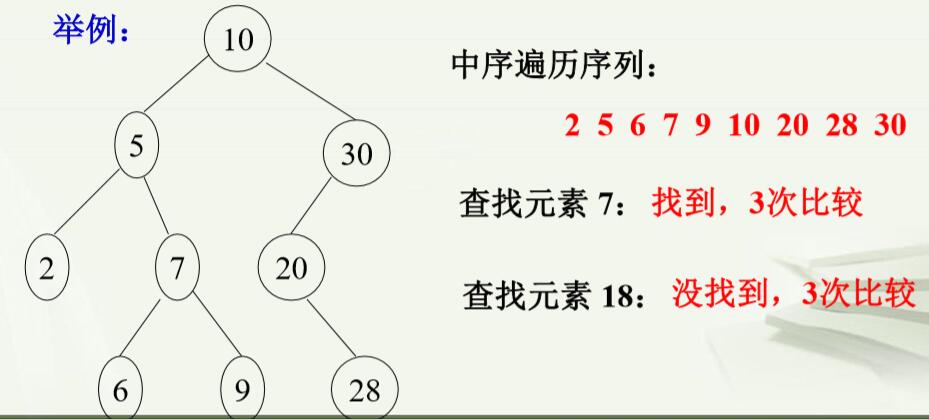
数据结构：树与二叉树（三） 特殊二叉树 　　这片博客讲一下二叉树中的几种特殊二叉树。 　　一、二叉排序树 　　1.定义 　　2.递归定义 　　3.特点 　　4.二叉排序树的构建（创造） 　　二、堆 　　1.定义 　　2.特点 　　3.堆的用途 　　4.堆的构造（创建） 　　三、最优二叉树 　　1.基本概念 　　2.最优二叉树（哈弗曼树,Huffman树）定义 　　3.最优二叉树的创造（构建） 　　4.最优二叉树的应用——Huffman编码 　　一、二叉排序树（Binary Sort Tree,BST） 　　1.定义：二叉树中，任何结点均满足条件：“大于其左子树上的所有结点，小于其右子树上的所有结点（若存在的话）”。又称为二叉查找树，或二叉搜索树。 　　2.递归定义：若二叉树是空，则是二叉排序树，否则：若左子树不空，它的结点均小于根结点；若右子树不空，它的结点均大于根结点；左右子树又都是二叉排序树。 　　3.特点： 　　（1）可以实现类似折半思想的查找，有较高的查找性能； 　　（2）中序遍历二叉排序树，可以得到一个有序序列。 　　
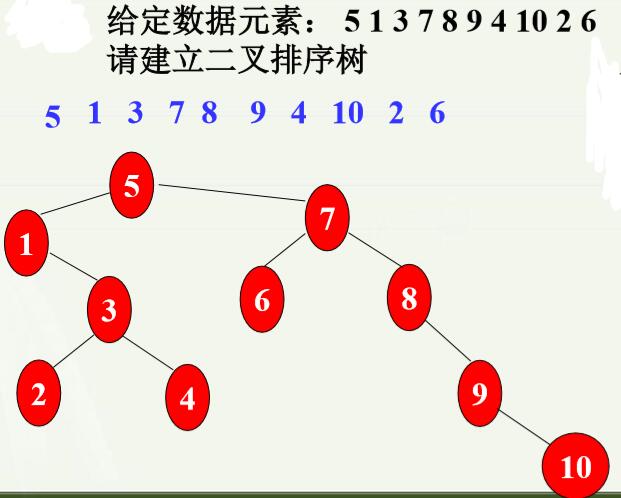
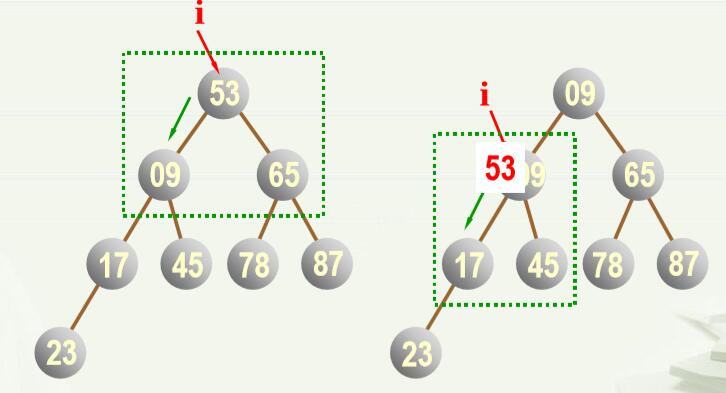
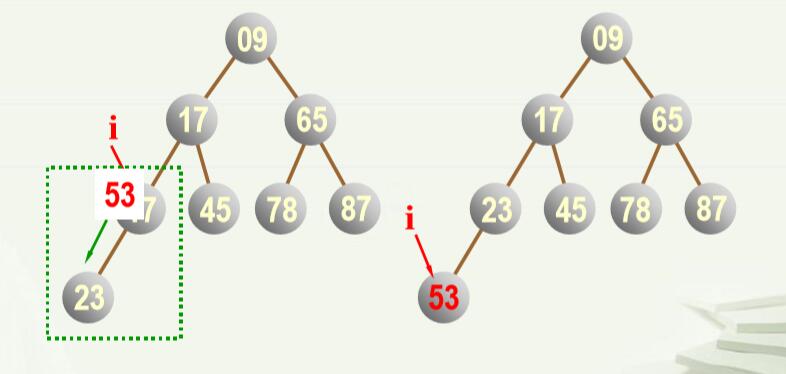
　　4.二叉排序树的构建（创造） 　　因为二叉排序树的特殊性质，所以其创建方法比较简单（左小右大）。 　　（1）基本思想：只需将数据素链到合适的位置（满足其特殊性质）。 　　（2）创建方法： 　　开始二叉树为空，然后重复在二叉树中插入素，即： 　　读入数据结点； 　　①若二叉树为空，则该结点为树的根结点；显然是二叉排序树； 　　②若二叉树不是空，则与根做比较，若比根大则在右子树中插入，否则在左子树中插入。 　　重复②中步骤，直到所插入结点成为树的叶子结点。 　　二叉排序树，最主要的操作就是创建和删除，对于创建，给定一个数据序列，要根据该序列创建二叉树，例如： 　　
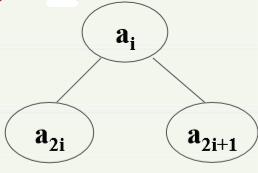
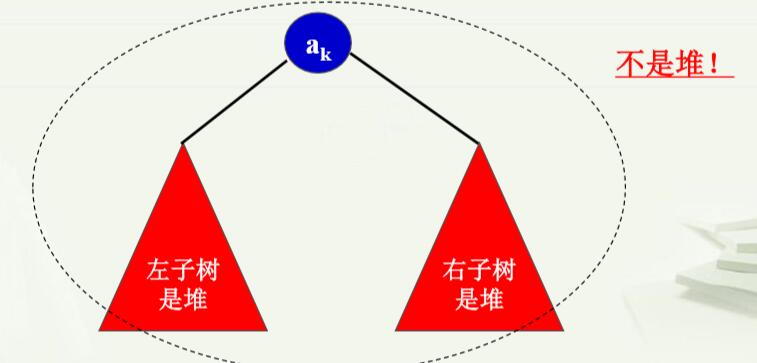
　　至于操作的具体实现，这里就不写了，很简单，有兴趣的童鞋可以问一下度娘。 　　二、堆（Heap） 　　在许多应用中（例如优先队列），需要从数据集中挑选具有最小或最大关键码的素。找最小或最大素的常用算法的思想就是“打擂台”（就是将数据素排队一个一个来，如果当前素比擂台上的素更大或更小，则将该素扶上擂台，原先在擂台上的素则舍弃），其时间复杂性为O(n)。那么有没有更好的算法呢？ 　　“堆”是一种特殊的二叉树数据结构，在它上面可以有高效的求最小（或最大）值操作。 　　1.定义：n个数据素的序列a1,a2,a3,…,an，当且仅当满足下列关系是为堆。又称为二叉堆，Binary Heap 　　ai<a(2*i)        ai<=a(2*i+1) ——最小堆   或者   ai>a(2*i)        ai>=a(2*i+1) ) ——最大堆 　　
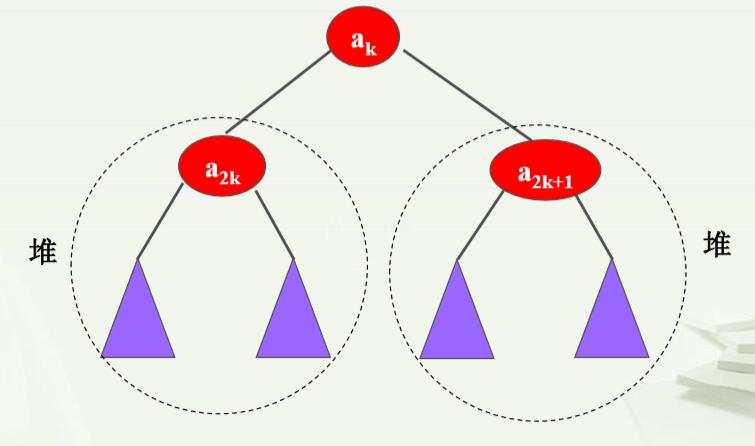
　　堆可以用一棵完全二叉树来表示，更直观。即以n个数据素的序列a1,a2,a3,…,an按照从第一层开始，每层从左向右构造出完全二叉树，如果任一结点的素值都不大于（或不小于）它的左右孩子的素值，则该完全二叉树就是最小堆（最大堆）。 　　2.特点： 　　（1）在最小堆中，最小的素一定是根结点素，最大素可能在最右结点素； 　　（2）在最大堆中，最大的素也一定是根结点素，最小素咋不一定在哪里。 　　
　　3.堆的用途： 　　（1）高效求最小（最大）值（在堆顶）。如果一个序列（完全二叉树）不是堆，则通过调整把它变成堆，于是就得到了最小（或最大）素。 　　（2）不断地重复求最小（或最大）值，可以实现排序。——堆排序 　　4.堆的构造（创建） 　　（1）假设a(k+1)…a(m)满足堆的性质，即它是堆，而a(k)a(k+1)…a(m)不是堆，那么如何将其调整为堆？ 　　
　　
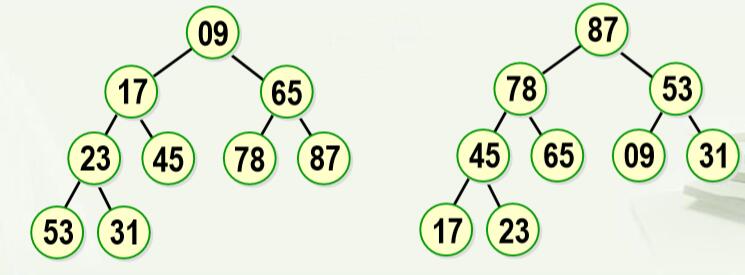
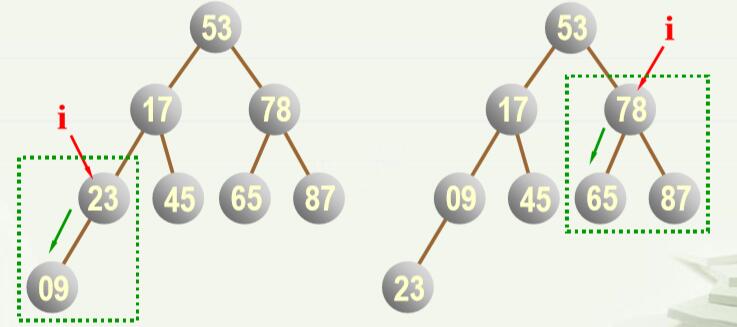
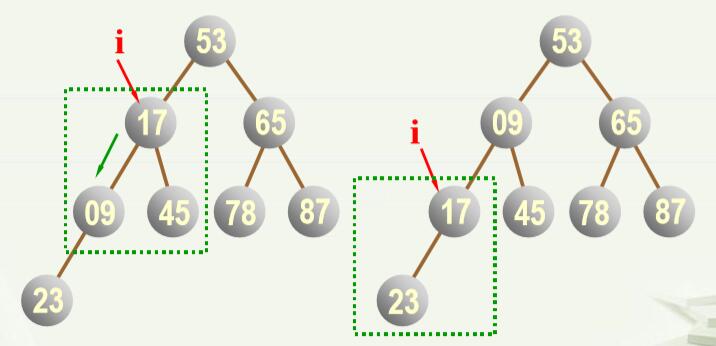
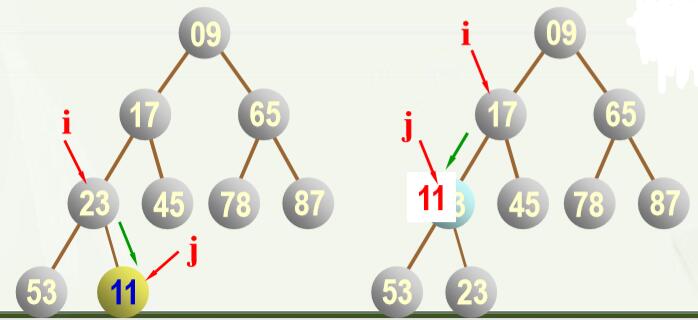
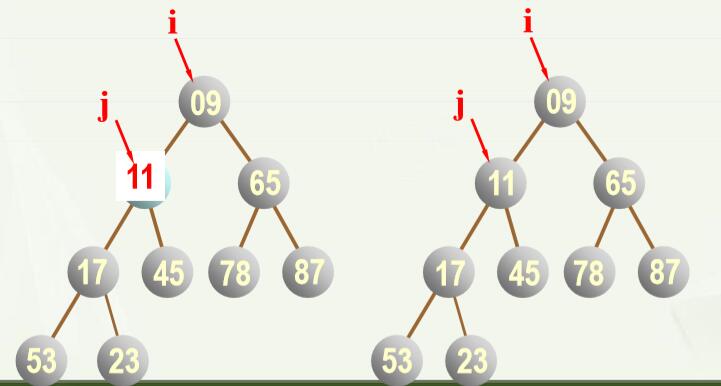
　　（2）具体的调整步骤为，按“自上而下”的顺序调整： 　　堆顶素a(k)与左右子树的根结点(a(2*k),a(2*k+1))比较（即只要与小根比较即可）： 　　①若a(k)比小根小，则是堆（最小堆），结束； 　　②否则，即a(k)比小根大，则与小根交换。但可能会导致小根所在的子树的堆性质被破坏，如果被破坏，就用同样的方式进行调整，知道调整的子树已经是堆或为叶子为止。 　　即循环执行①②步骤（一个while循环）。 　　（3）假设a1…a(n)是任意一个序列，如何调整为堆呢？ 　　老师PPT里讲的调整方法我反复看了，感觉有点问题，而且有点啰嗦，不过也可能是我没看明白，我就说一下自己的看法吧。 　　如果一个任意序列（任意一棵完全二叉树）要调整为堆，那么可以自下而上逐步调整，假设要调整为最小堆： 　　从叶子结点开始，将每个结点与其根结点作比较，如果值比根结点小，则将该结点与根结点互换，由此重复，直到换到根结点。然后再重复上述过程（即再从叶子结点开始比较），如果所有结点均与其根结点比较过后并未发生任何换位，则此堆调整完成。 　　放一组图，大家看了就明白了。 　　
　　
　　
　　
　　（4）堆的插入删除，与二叉排序树的思想大致相同，这里就不说了。当然，插入过后还是需要调整的。因为插入素后，可能会破坏堆，调整的方法，与（3）中相同，不过只需要调整插入的那个节点即可。给大家放一组图。 　　
　　
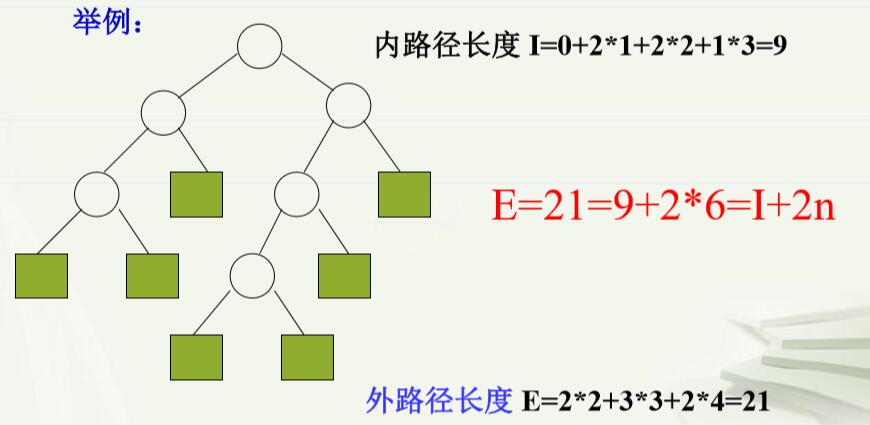
　　删除堆顶素，一般是用最后一个素来替换堆顶素。当然，替换过后，也可能会破坏堆，只需要按照（3）中的方法调整即可。 　　三、最优二叉树 　　1.基本概念 　　（1）路径：结点序列n1,n2,….nk满足n(i)是n(i+1)的双亲。 　　（2）路径长度：路径上的分支数。 　　（3）扩充二叉树：在一般二叉树中，将原来的每个空指针都指向一个特殊的结点——外结点（原来二叉树中的结点称为内结点），这样的二叉树称为扩充二叉树（真二叉树）。 　　特点：在扩充二叉树中没有度为1的结点。 　　外结点个数=内结点个数+1 　　（4）树的内路径长度：从根结点到各个内结点的路径长度之和。 　　
　　树的外路径长度：从根结点到各个外结点的路径长度之和。 　　
　　E = I + 2*n 　　举例： 　　
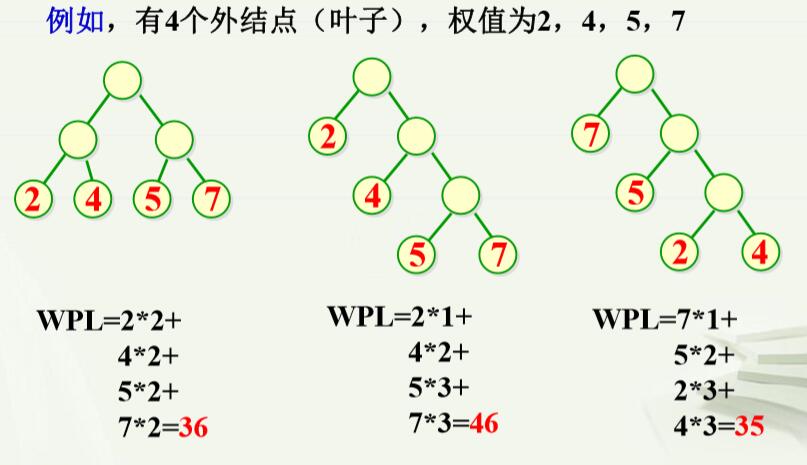
　　（5）结点的权：有时为了表示某种含义，赋予结点一个数值。 　　（6）结点加权路径长度：从根结点到该结点的路径长度与权值之积，即w(i)*l(i)。 　　（7）扩充二叉树的加权路径长度(Weighted Path Length, WPL)：假设给扩充二叉树的外结点（扩充后的叶子）赋予权值， 则二叉树中所有加权结点的加权路径长度之和称为扩充二 叉树的加权路径长度。 　　
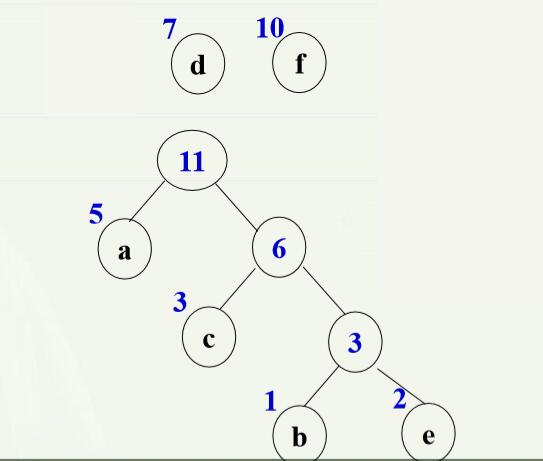
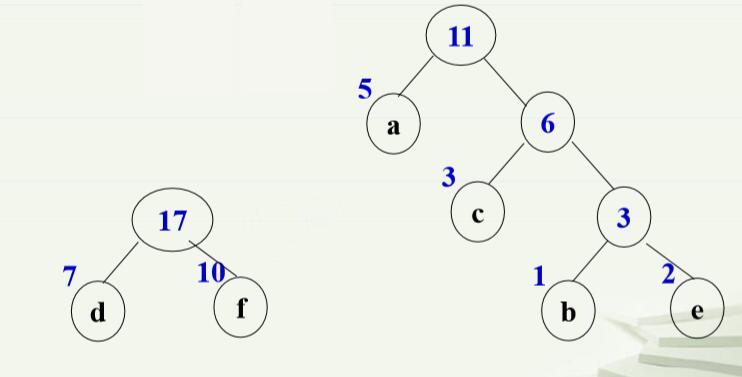
　　2.最优二叉树（哈弗曼树,Huffman树）定义：假设有n个数据素，他们的全是分别为w1,w2,…,w(n)，以它们为叶子构造具有n个叶子的（真）二叉树（可以构造很多棵）。加权路径最小的二叉树称为最优二叉树（哈弗曼树）。 　　特点：权值大的应该尽可能靠近根。 　　举例： 　　
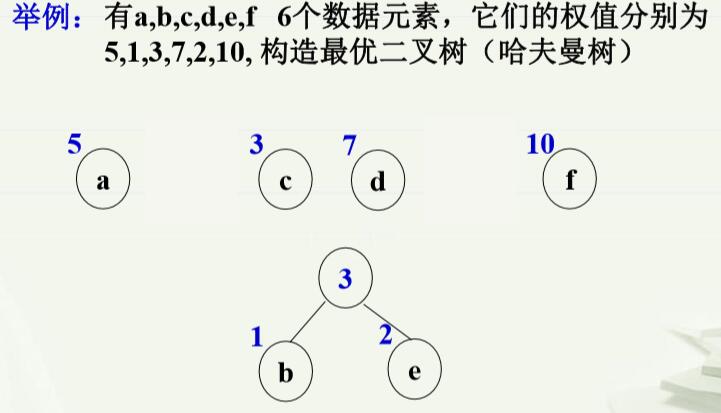
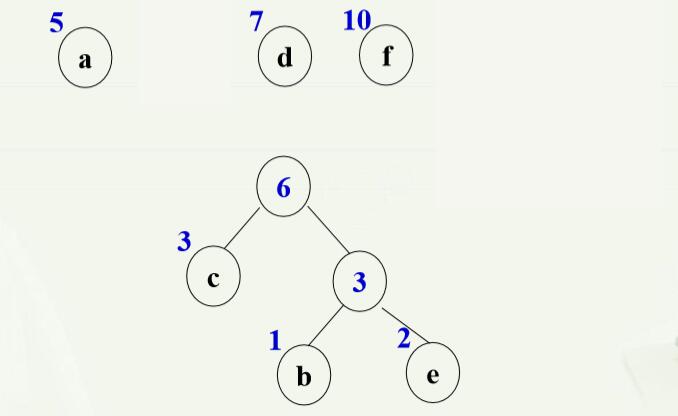
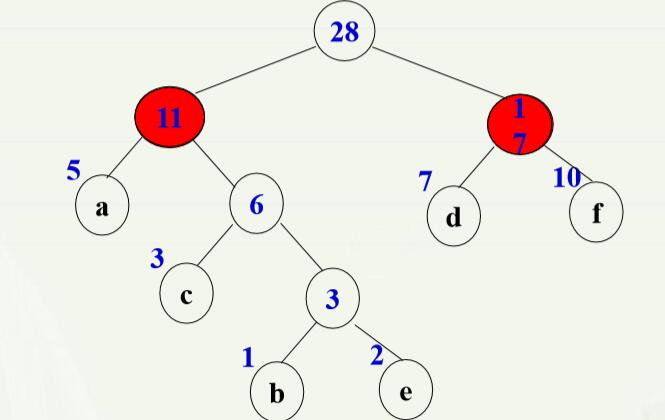
　　3.最优二叉树的创造（构建） 　　（1）基本思想：选择权值小的叶子，让它离根的距离尽可能远（贪心算法）。 　　（2）算法描述： 　　①由给定 n 个权值 {w0, w1, w2, …, w(n-1)}，构造具有 n 棵扩 充二叉树的森林 F = { T0, T1, T2, …, Tn-1 }，其中每棵扩 充二叉树 Ti 只有一个带权值 wi 的根结点, 其左、右子树 均为空; 　　②重复以下步骤，直到F中仅剩一棵树为止： 　　在 F 中选取两棵根结点的权值最小的扩充二叉树,    做 为左、右子树构造一棵新的二叉树。置新的二叉树的根结点的权值为其左、右子树上根结点的权值之和。 　　·在F中删去这两棵二叉树。 　　·把新的二叉树加入F。 　　说实话，这上面的描述是在太绕口了，我读了好几遍才明白，说白了，这个算法就是先将权值最小的两个结点作为叶子结点，其根结点的权值是这两个结点的权值相加，如果等待的结点中有与这个相加后的权值相等的结点，就作为这个根结点的兄弟结点，然后依次累加上去，知道最终的root结点。 　　举个例子： 　　
　　
　　
　　
　　
　　当然， 这种方法构造的最优二叉树不一定是唯一的，因为左右子树可以互换。 　　4.最优二叉树的应用——Huffman编码 　　早期，电报是进行快速、远距离通讯的重要手段。 　　
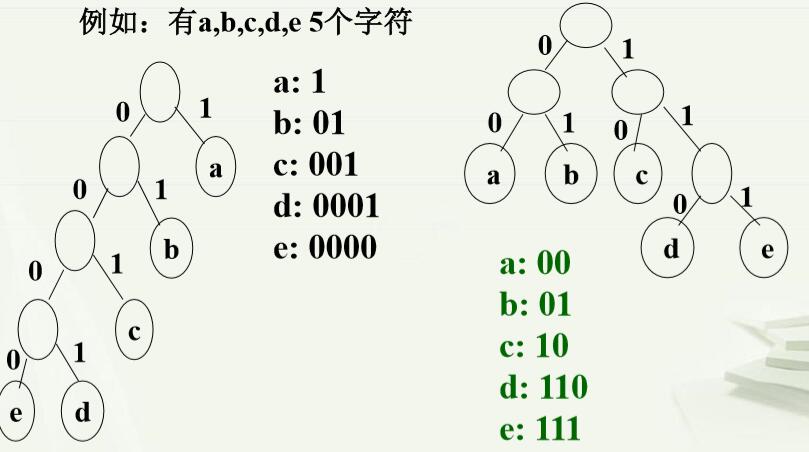
　　实现电报通讯的两个要素： 　　①一套编码，可以将电文编码为待发送的电文，还可以把收到的电文译码为原电文。 　　②发送的电文应尽可能短，节省占用线路费用。 　　编码的原则： 　　首先，译码要唯一，即对字符进行编码后，能够唯一地翻译成原来的字符；其次，各个字符的编码要尽可能短，只有这样才能使编码后最短。 　　编码的方法： 　　定长编码方法——特点：易达到译码唯一，但长度较大；ASCII编码是定长编码； 　　不定长编码方法——特点：长度较短，但达到译码唯一较难。 　　（1）哈夫曼编码的方法——不定长编码方式 　　前缀码：任何一个字符的编码都不是另外字符编码的前缀。 　　构造方法：用被编码的字符作为叶子，构造二叉树，然后在二叉树的做分支上标“0”，右分支标“1”（或反过来），每个字符的编码就是从根到该字符叶子所经过路径上的0、1序列。 　　这样构造出来的一套编码一定是前缀码，译码唯一。 　　（2）举例： 　　
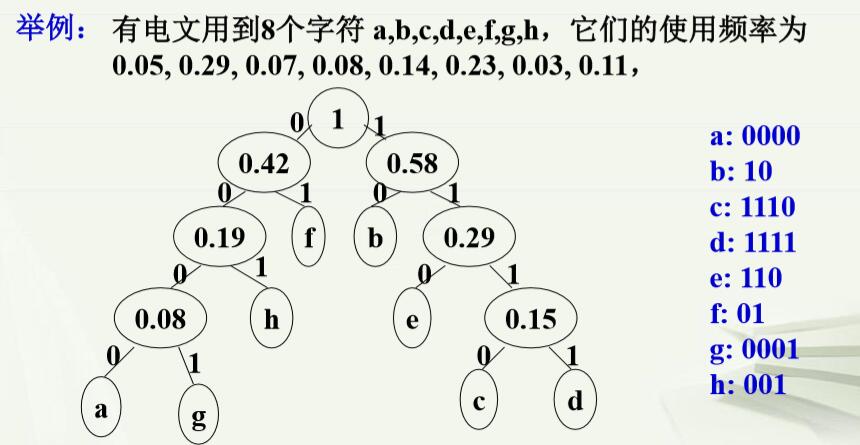
　　（3）使编码最短的方法——哈夫曼树 　　要是电文的编码长度最短，应该使用频率高的字符，编码应该短，可以使用频率作为权值，构造编码字符为叶子的哈夫曼树（二叉树），使用频率高的字符，离根近，编码短。从而，电文编码达到最短（而且是前缀码）。 　　因此，一棵最优二叉树就同时解决了译码唯一和编码长度最短 的问题，由Huffman树得到的这套编码称为Huffman编码。 　　举例：