【音频带背】数据结构考前必背简答题系列（二）：树与二叉树 抓码计算机考研将陆续推出数据结构、计网、计组、操作系统的必背文本及音频，文本由抓码专业团队的学长姐精心梳理，单篇推送后会推出PDF合集，帮助正在冲刺备考的你提高学习效率。 此外，抓码运营小组将根据你的需求制作音频或视频带背，方便大家利用碎片化时间随时随地回顾知识点，以更多形式帮助你更好地冲刺备考。 1.简述一棵度为2的有序树与一棵二叉树有何区别？ 一棵度为2的有序树与一棵二叉树的区别在于: 有序树的结点次序是相对于另一结点而言的，如果有序树中的子树只有一个孩子时，这个孩子结点就无须区分其左右次序。 而二叉树无论其孩子数是否为2，均需确定其左右次序，也就是说二叉树的结点次序不是相对于另一结点而言而是确定的。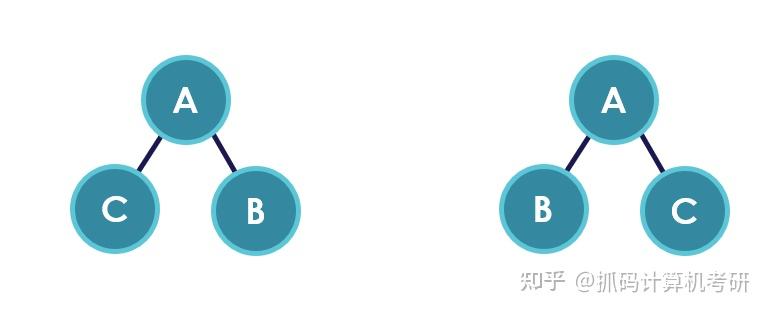
图 1 这是两棵不同的二叉树 2 简述满二叉树，完全二叉树，二叉排序树，平衡二叉树的特性 满二叉树： ❶高度为H，结点数为2H-1的二叉树为满二叉树。 ❷满二叉树一定是完全二叉树。
图 2 三层满二叉树 完全二叉树： ❶除最后一层外，其余各层的节点数量达到最大值，并且最后一层只能在右侧缺少节点。 ❷若有度为1的结点，则只可能有一个，且该结点只有左孩子而无右孩子。
图 3 具有6个结点的完全二叉树 二叉排序树： ❶左子树上所有的关键字均小于根结点，右子树上所有关键字均大于根结点。左子树和右子树又分别是一棵二叉排序树。 ❷构造二叉排序树时，用两组相同的数据，若数据的排列顺序不同，构造出的二叉排序树也不一样。 ❸二叉排序树的叶子结点到根结点的路径不一定是有序的。
图 4 一棵二叉排序树 平衡二叉树： 树中每一个结点的左子树，右子树高度之差的绝对值小于等于1。 3 3 树的存储结构有哪些? ❶双亲表示法：采用一组连续的存储空间存储每个结点，同时在每个结点后面增设一个伪指针指向其双亲节点。 ❷孩子表示法：将每个结点的孩子结点用单链表链接起来形成一个线性结构。 ❸孩子兄弟表示法：以二叉链表作为树的存储结构，其左指针指向第一个孩子结点，右指针指向其 ❹相邻的兄弟结点。可以方便地实现树转换为二叉树的操作，易于查 找结点的孩子等，但缺点是从当前结点查找其双亲结点比较麻烦。 4 一棵深度为的满叉树有如下性质:第层上的结点都是叶子结点，其余各层上 每个结点都有棵非空子树,如果按层次自上至下，从左到右顺序从1开始对全部结点编号， 回答下列问题: (1)各层的结点数目是多少? (2)编号为的结点的父结点如果存在，编号是多少? (3)编号为的结点的第i个孩子结点如果存在，编号是多少? (4)编号为的结点有右兄弟的条件是什么?其右兄弟的编号是多少? ❶第i层上的结点数目是mi-1。 ❷编号为n的结点的父结点如果存在，编号是((n-2)/m)+1。 ❸编号为n的结点的第i个孩子结点如果存在，编号是(n-1)*m+i+1。 ❹编号为n的结点有右兄弟的条件是(n-1)%m≠0。其右兄弟的编号是n+1。 5 二叉树结点的数量关系 ❶在二叉树的第 i 层上至多有2(i-1)个结点(i≥1) ❷深度为k的二叉树上至多含2k-1个结点（k≥1） ❸结点关系：n0=n2+1 (n0+n1+n2=1+n1+2n2) 6 二叉树的确定 ❶二叉树的前序+中序可以唯一的确定一棵二叉树 ❷二叉树的后序+中序可以唯一的确定一棵二叉树 ❸二叉树的层序+中序可以唯一的确定一棵二叉树 7 为什么会引入线索二叉树？它有什么优势？ 发明原因：含有n个结点的二叉链表中，含有n+1个空链域（n个结点有2n个链域，由于没有链域指向根结点，故含有n+1个空链域）。故用二叉链表构造二叉树会造成大量存储空间的浪费，所以利用空链域指向该结点在某种遍历下的前驱或后继结点可以有效利用空间。 优点：为了加快查找前驱和后继结点的速度 8 简述什么是哈夫曼树？ 权：树中的结点往往被赋予一个有意义的数值称为该结点的权。 结点的带权路径长度：从树的根到任意节点的路径长度与该结点的权值之积称为该结点的带权路径长度。 树的带权路径长度：树中所有叶结点的带权路径之和为该树的带权路径长度。 哈夫曼树：带权路径长度最小的树为哈夫曼树 9 简述构造哈夫曼树的算法 将树中的每个结点都看成一个独立的二叉树构成森林F，从F中选择根结点最小的两棵树构成一棵新的二叉树，二叉树的根结点为两个结点之和，并将这两个树从F中删除，将新构成的树并入F中，重复上述过程，直到F中只剩下一个树。 特点：哈夫曼树中不存在度为1的结点，权值越小的结点距离根结点的路径长度越大。 所有字符结点出现在叶子结点的位置，一般用0标记往左，1标记往右(这个标记可以自己选择，题目中没有标明时，自己注明)。 10 证明完全二叉树的每棵子树也都是完全二叉树。 证明:设T是一棵完全二叉树，S是它的一棵子树。由子树定义可知,S是由T中某个节点及其所有子孙构成的。由于T是完全二叉树，T的所有叶子节点都在两个相邻的层次上，因此，S的所有叶子节点都在两个相邻的层次上。类似的，如果在S中存在不位于底层上的节点层，那么，该层也不位于T的底层上，它必须在T中所有底层叶子节点的右边，因此它也必须在S中所有底层叶子节点的右边，从而得到S是完全二叉树。
2024最新激活全家桶教程，稳定运行到2099年，请移步至置顶文章：https://sigusoft.com/99576.html
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请联系我们举报，一经查实，本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处：https://sigusoft.com/80547.html
