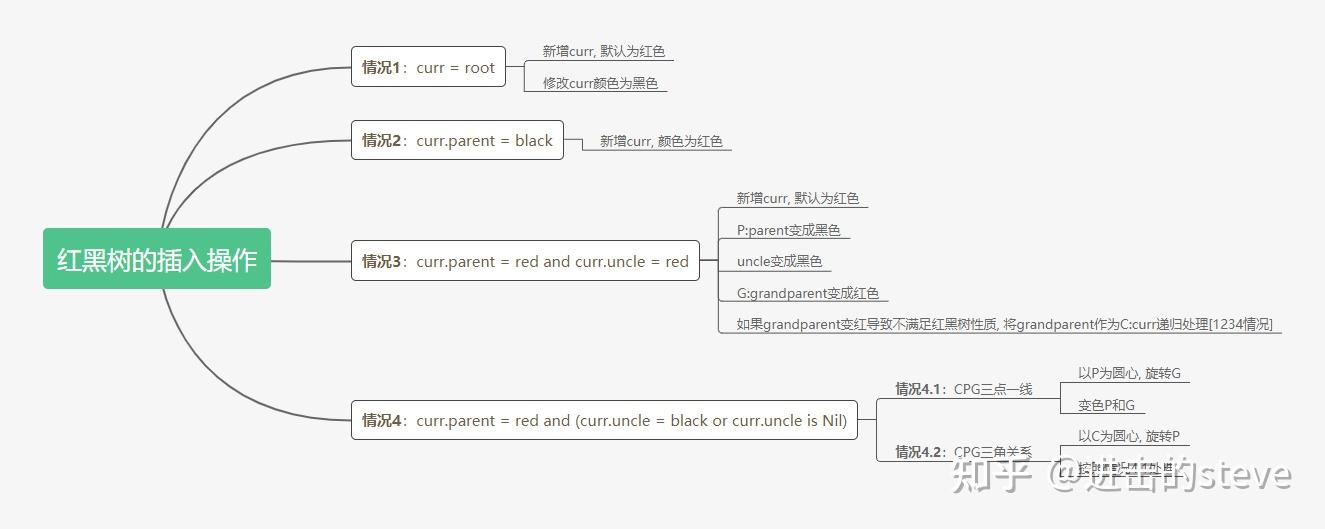
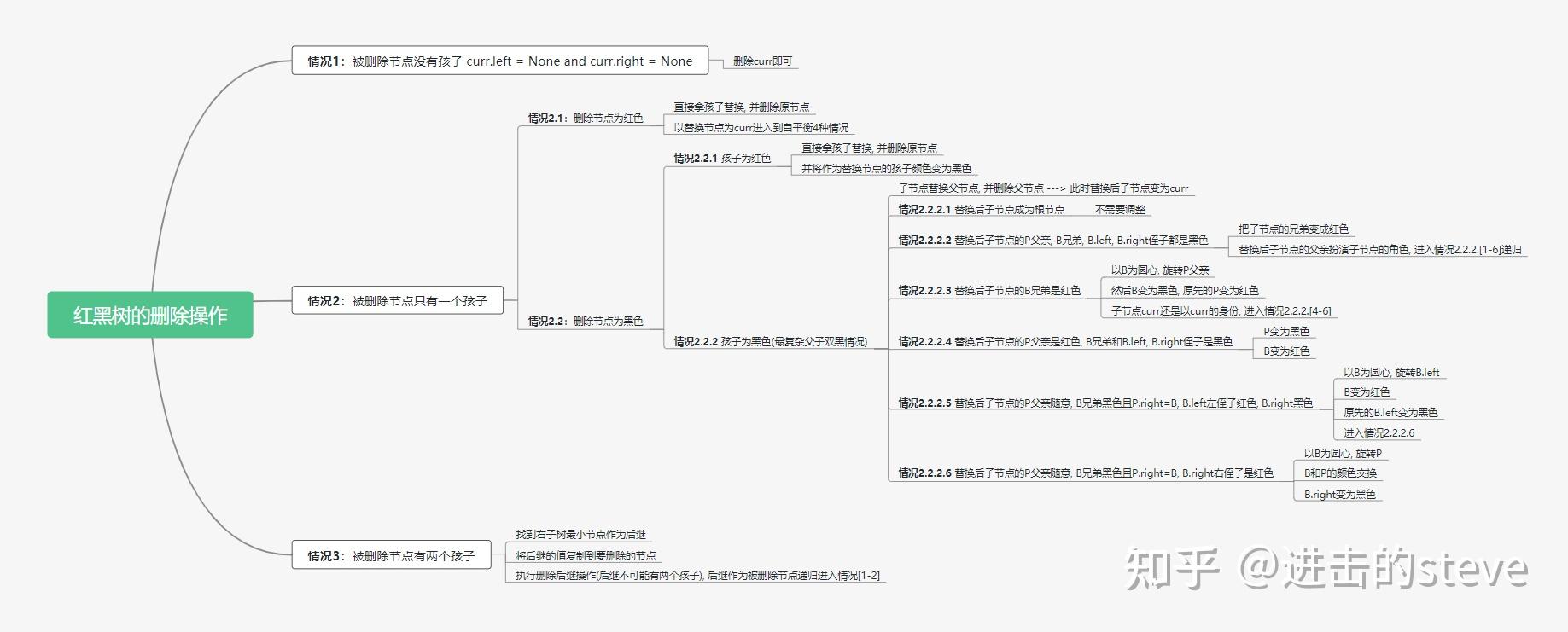
红黑树超全讲解纯干货带流程图方便收藏 红黑树的概念？什么是红黑树？ 红黑树是一种含有红黑节点并能自平衡的二叉查找树。区别于avl树, avl树是完美平衡二叉树, 红黑树是弱平衡二叉树。 红黑树的五大性质（最核心） 每个节点要么是黑色, 要么是红色。.根节点是黑色。 —> 硬性规定, 无法推导出这个结论每个叶子节点(Nil)是黑色。 —> 叶子节点都是黑色虚节点(color=black;value=None)每个红色节点的两个子节点一定都是黑色(父节点也是黑色)。任意一个节点到每个叶子节点的路径都包含相同数量的黑节点。 (红黑树不是完美平衡, 但是黑色完美平衡) 红黑树的规律（由五大性质推导出） 结论：性质4 5作为约束可以保证任意节点到每个叶子节点路径最长不会超过最短路径的2倍 原因：最极端情况下：出现最短路径时, 这条路径必然都是黑节点; 出现最长路径时, 这条路径必然是红黑节点相间构成, 此时路径上红节点数量=黑节点数量; 再结合性质5, 极端情况下最长路径也仅仅是最短路径的两倍。 红黑树的操作 红黑树自平衡的原子操作：变色, 旋转(圆心, 方向) 红黑树的插入操作 思路：每次插入之后要操作保持红黑树的性质。1. 查找插入的位置 2.插入后自平衡 自平衡的4种情况：(设curr为当前节点) 情况1：curr = root新增curr, 默认为红色修改curr颜色为黑色 情况2：curr.parent = black新增curr, 颜色为红色 情况3：curr.parent = red and curr.uncle = red新增curr, 默认为红色P:parent变成黑色uncle变成黑色G:grandparent变成红色如果grandparent变红导致不满足红黑树性质, 将grandparent作为C:curr递归处理[1234情况] 情况4：curr.parent = red and (curr.uncle = black or curr.uncle is Nil) — 情况4.1：CPG三点一线— 以P为圆心, 旋转G— 变色P和G — 情况4.2：CPG三角关系— 以C为圆心, 旋转P— 按照情况4.1处理
红黑树的插入操作 红黑树的删除操作 思路：如果被删除节点没有孩子，直接删除即可。如果删除节点只有一个孩子：1.删除节点为红色时, 直接拿孩子补位即可; 2.删除节点为黑色时, 2.1.孩子为红色, 直接拿孩子替换并将孩子染成黑色; 2.2.孩子为黑色则复杂得多。如有两个孩子, 则先要找到该节点前驱(左子树最大)或者后继(右子树最小), 习惯上一般选择后继, 这里我们用后继。然后前驱或后继的值复制到要删除的节点, 最后删除前驱或后继。由于前驱和后继不可能有两个孩子, 删除前驱后继=删除只有一个孩子或没有孩子的节点。 情况1：被删除节点没有孩子 curr.left = None and curr.right = None删除curr即可 情况2：被删除节点只有一个孩子 — 情况2.1：删除节点为红色— 直接拿孩子替换, 并删除原节点— 以替换节点为curr进入到自平衡4种情况 — 情况2.2：删除节点为黑色 ——- 情况2.2.1 孩子为红色——- 直接拿孩子替换, 并删除原节点——- 并将作为替换节点的孩子颜色变为黑色 ——- 情况2.2.2 孩子为黑色(最复杂父子双黑情况)——- 子节点替换父节点, 并删除父节点 —> 此时替换后子节点变为curr ———– 情况2.2.2.1 替换后子节点成为根节点———– 不需要调整 ———– 情况2.2.2.2 替换后子节点的P父亲, B兄弟, B.left, B.right侄子都是黑色———– 把子节点的兄弟变成红色———– 替换后子节点的父亲扮演子节点的角色, 进入情况2.2.2.[1-6]递归 ———– 情况2.2.2.3 替换后子节点的B兄弟是红色———– 以B为圆心, 旋转P父亲———– 然后B变为黑色, 原先的P变为红色———– 子节点curr还是以curr的身份, 进入情况2.2.2.[4-6] ———– 情况2.2.2.4 替换后子节点的P父亲是红色, B兄弟和B.left, B.right侄子是黑色———– P变为黑色———– B变为红色 ———– 情况2.2.2.5 替换后子节点的P父亲随意, B兄弟黑色且P.right=B, B.left左侄子红色, B.right黑色———– 以B为圆心, 旋转B.left———– B变为红色———– 原先的B.left变为黑色———– 进入情况2.2.2.6 ———– 情况2.2.2.6 替换后子节点的P父亲随意, B兄弟黑色且P.right=B, B.right右侄子是红色———– 以B为圆心, 旋转P———– B和P的颜色交换———– B.right变为黑色 (讨论：为何情况2.2.2.5和2.2.2.6都能保证P.right=B? —> 情况2.2.2.3的操作) 情况3：被删除节点有两个孩子找到右子树最小节点作为后继将后继的值复制到要删除的节点执行删除后继操作(后继不可能有两个孩子), 后继作为被删除节点递归进入情况[1-2]
红黑树的删除操作 复杂度分析 毫无疑问，红黑树和avl树没有理用额外空间，所以他们空间复杂度都为O(1) avl树和红黑树查询时间复杂度均为O(logn)平均查询时间红黑树稍微慢一点但是没慢多少。虽然对于插入和删除节点, avl树和红黑树最坏情况下时间复杂度均为O(logn), 但在自平衡的时候, 红黑树由于有黑色节点的存在(上文中自平衡的情况2), 每次parent为黑色时复杂度降为O(1)。根据性质4 5 得出红黑树的每条路径上黑节点数量 大于等于 红节点数量, 所以至少50%的概率parent为黑色。所以红黑树自平衡的平均时间复杂度 小于等于 avl树平均时间复杂度的一半。
2024最新激活全家桶教程，稳定运行到2099年，请移步至置顶文章：https://sigusoft.com/99576.html
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请联系我们举报，一经查实，本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处：https://sigusoft.com/78059.html
