fft 计算_FFT原理通俗易懂FFT原理史上最精炼解读本文主要复习一下FFT,虽然有很多博客书籍介绍FFT,但是个人认为还是介绍的稍微有一些复杂,本文将尽可能用最简单的方法来把其原理阐述清楚。首先给一个概念介绍:FFT是DFT的一种快速算法,DFT:离散傅里叶变换,这里假定
FFT原理史上最精炼解读 本文主要复习一下FFT, 虽然有很多博客书籍介绍FFT,但是个人认为还是介绍的稍微有一些复杂,本文将尽可能用最简单的方法来把其原理阐述清楚。 首先给一个概念介绍: FFT是DFT的一种快速算法,DFT:离散傅里叶变换,这里假定读者知道DFT。 先给出DFT公式:
![fft 计算_FFT原理通俗易懂插图1 X[k]=\sum_{n=0}^{N-1}x[n]e^{\frac{-j2\pi kn}{N}}](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) 其中k取值范围也是0到N-1的离散点,可见按照常规方法计算k=0到N-1的值,大约要计算N*N次乘法,算法复杂度为O(N^2),复杂度较高,FFT就被发明出来加速计算 下面我们来解释FFT算法,首先为了简化公式,我们记:
其中k取值范围也是0到N-1的离散点,可见按照常规方法计算k=0到N-1的值,大约要计算N*N次乘法,算法复杂度为O(N^2),复杂度较高,FFT就被发明出来加速计算 下面我们来解释FFT算法,首先为了简化公式,我们记:
 同时,我们只考虑N为2的次幂的情形(这也是一般的FFT考虑的情形,对于非2的指数次幂,有一些特殊处理方法,这里为了简化我们不考虑) 先给出
同时,我们只考虑N为2的次幂的情形(这也是一般的FFT考虑的情形,对于非2的指数次幂,有一些特殊处理方法,这里为了简化我们不考虑) 先给出
 的三个性质: 1,周期性
的三个性质: 1,周期性
 其中k,t是任意整数;证明 :据
其中k,t是任意整数;证明 :据
 即可得 2,
即可得 2,
 证明:根据
证明:根据
 即可得 3,
即可得 3,
 证明:显然成立 这三个性质,我们在后面会用到,后文中称为 “性质1”,“性质2”和“性质3” 那么,DFT公式简化为:
证明:显然成立 这三个性质,我们在后面会用到,后文中称为 “性质1”,“性质2”和“性质3” 那么,DFT公式简化为:
![fft 计算_FFT原理通俗易懂插图17 X[k]=\sum_{n=0}^{N-1}x[n]W_N^{kn}](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) 我们将n 按照偶数和奇数归类, 先把n为偶数的项求和,再把奇数项求和;令
我们将n 按照偶数和奇数归类, 先把n为偶数的项求和,再把奇数项求和;令
![fft 计算_FFT原理通俗易懂插图19 G[k]=\sum_{n=0}^{N-2}x[n]W_N^{kn}](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) n为偶数
n为偶数
![fft 计算_FFT原理通俗易懂插图21 H[k]=\sum_{n=1}^{N-1}x[n]W_N^{kn}](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) n为奇数 则,显然
n为奇数 则,显然
![fft 计算_FFT原理通俗易懂插图23 X[k]=H[k]+G[k]](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) 下面,我们考察 X[k+N/2] ,根据DFT公式,有
下面,我们考察 X[k+N/2] ,根据DFT公式,有
![fft 计算_FFT原理通俗易懂插图25 X[k+N/2]=\sum_{n=0}^{N-1}x[n]W_N^{n(k+N/2)}](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) 将等式右边的求和分为n为偶数项的和,与n为奇数项的和,有 偶数项:
将等式右边的求和分为n为偶数项的和,与n为奇数项的和,有 偶数项:
![fft 计算_FFT原理通俗易懂插图27 \sum_{n=0}^{N-2}x[n]W_N^{n(k+N/2)}=\sum_{n=0}^{N-2}x[n]W_N^{nk+n*N/2} (1)](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) 因为n是偶数,利用性质1,有
因为n是偶数,利用性质1,有
![fft 计算_FFT原理通俗易懂插图29 (1)=\sum_{n=0}^{N-2}x[n]W_N^{nk} = G[k]](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) 奇数项:
奇数项:
![fft 计算_FFT原理通俗易懂插图31 \sum_{n=1}^{N-1}x[n]W_N^{n(k+N/2)}=\sum_{n=1}^{N-1}x[n]W_N^{nk+(n-1)*N/2+N/2} (2)](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) 因为此时n为奇数,利用性质1,和性质2,有
因为此时n为奇数,利用性质1,和性质2,有
 =-H[k]](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) 综上,
综上,
![fft 计算_FFT原理通俗易懂插图19 G[k]=\sum_{n=0}^{N-2}x[n]W_N^{kn}](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) n取偶数
n取偶数
![fft 计算_FFT原理通俗易懂插图21 H[k]=\sum_{n=1}^{N-1}x[n]W_N^{kn}](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) n取奇数
n取奇数
![fft 计算_FFT原理通俗易懂插图23 X[k]=H[k]+G[k]](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E)
![fft 计算_FFT原理通俗易懂插图35 X[k+N/2]=G[k]-H[k]](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) 这就意味着,我们只需计算X[0],X[1],,,X[N/2-1] 对应的H[k]和G[k],之后这些计算结果可以复用到X[k+N/2]的计算,从而减小了计算量 进一步,我们来化简化一下G[k],H[k],利用性质3,有
这就意味着,我们只需计算X[0],X[1],,,X[N/2-1] 对应的H[k]和G[k],之后这些计算结果可以复用到X[k+N/2]的计算,从而减小了计算量 进一步,我们来化简化一下G[k],H[k],利用性质3,有
![fft 计算_FFT原理通俗易懂插图37 G[k]=\sum_{r=0}^{N/2-1}x[2r]W_N^{2kr} =\sum_{r=0}^{N/2-1}x[2r]W_{N/2}^{rk}](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E)
![fft 计算_FFT原理通俗易懂插图39 H[k]=\sum_{r=0}^{N/2-1}x[2r+1]W_N^{k(2r+1)} =W_N^k\sum_{r=0}^{N/2-1}x[2r+1]W_{N/2}^{rk}](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) 我们单独的看G[k]和H[k]的表达式,发现它们分别各是一个标准的DFT(其中H[k]是在DFT的结果上乘以了一个系数因子
我们单独的看G[k]和H[k]的表达式,发现它们分别各是一个标准的DFT(其中H[k]是在DFT的结果上乘以了一个系数因子
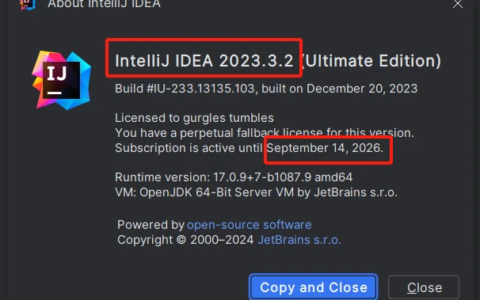
 ,其中k取值0到N/2-1) 这就意味着,我们通过FFT把一个阶为N的DFT分解为了两个阶为N/2的DFT,并在这个过程中减少了一半的计算量 显然,我们可以对分解后的两个DFT分别再继续分解下去(作图的话是一个标准的2叉树结构)如此,即得到FFT算法 虽然理论已经分析完毕,但是实际实现还是会有不少问题,首先,FFT是一个递归形式,由于递归涉及到入栈出栈,参数传递等,通常效率较低;最理想的自然是非递归实现;同时空间复杂度希望尽可能低。 笔者研究之后给出了如下比较理想的实现,测试已经通过,读者可以参考:https://github.com/wiltchamberian/FFT-Algorithm
,其中k取值0到N/2-1) 这就意味着,我们通过FFT把一个阶为N的DFT分解为了两个阶为N/2的DFT,并在这个过程中减少了一半的计算量 显然,我们可以对分解后的两个DFT分别再继续分解下去(作图的话是一个标准的2叉树结构)如此,即得到FFT算法 虽然理论已经分析完毕,但是实际实现还是会有不少问题,首先,FFT是一个递归形式,由于递归涉及到入栈出栈,参数传递等,通常效率较低;最理想的自然是非递归实现;同时空间复杂度希望尽可能低。 笔者研究之后给出了如下比较理想的实现,测试已经通过,读者可以参考:https://github.com/wiltchamberian/FFT-Algorithm
2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。
文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/75540.html
![fft 计算_FFT原理通俗易懂插图1 X[k]=\sum_{n=0}^{N-1}x[n]e^{\frac{-j2\pi kn}{N}}](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)







![fft 计算_FFT原理通俗易懂插图17 X[k]=\sum_{n=0}^{N-1}x[n]W_N^{kn}](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)
![fft 计算_FFT原理通俗易懂插图19 G[k]=\sum_{n=0}^{N-2}x[n]W_N^{kn}](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)
![fft 计算_FFT原理通俗易懂插图21 H[k]=\sum_{n=1}^{N-1}x[n]W_N^{kn}](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)
![fft 计算_FFT原理通俗易懂插图23 X[k]=H[k]+G[k]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)
![fft 计算_FFT原理通俗易懂插图25 X[k+N/2]=\sum_{n=0}^{N-1}x[n]W_N^{n(k+N/2)}](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)
![fft 计算_FFT原理通俗易懂插图27 \sum_{n=0}^{N-2}x[n]W_N^{n(k+N/2)}=\sum_{n=0}^{N-2}x[n]W_N^{nk+n*N/2} (1)](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)
![fft 计算_FFT原理通俗易懂插图29 (1)=\sum_{n=0}^{N-2}x[n]W_N^{nk} = G[k]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)
![fft 计算_FFT原理通俗易懂插图31 \sum_{n=1}^{N-1}x[n]W_N^{n(k+N/2)}=\sum_{n=1}^{N-1}x[n]W_N^{nk+(n-1)*N/2+N/2} (2)](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)
 =-H[k]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)
![fft 计算_FFT原理通俗易懂插图19 G[k]=\sum_{n=0}^{N-2}x[n]W_N^{kn}](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)
![fft 计算_FFT原理通俗易懂插图21 H[k]=\sum_{n=1}^{N-1}x[n]W_N^{kn}](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)
![fft 计算_FFT原理通俗易懂插图23 X[k]=H[k]+G[k]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)
![fft 计算_FFT原理通俗易懂插图35 X[k+N/2]=G[k]-H[k]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)
![fft 计算_FFT原理通俗易懂插图37 G[k]=\sum_{r=0}^{N/2-1}x[2r]W_N^{2kr} =\sum_{r=0}^{N/2-1}x[2r]W_{N/2}^{rk}](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)
![fft 计算_FFT原理通俗易懂插图39 H[k]=\sum_{r=0}^{N/2-1}x[2r+1]W_N^{k(2r+1)} =W_N^k\sum_{r=0}^{N/2-1}x[2r+1]W_{N/2}^{rk}](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)