用fft算法分析频谱_FFT频谱分析

MATLAB fft实现四大傅里叶分析　　〇、DFT离散傅里叶变换　　1. 介绍DFT 　　 DFT是一个完全与时间无关的纯粹数学运算，本身不具有任何物理意义，但它却是构成四种傅里叶分析的内核。并且由于DFT能够利用矩阵运算，并可借助FFT算法优化大大提升运算效率。　　
}X_ke^{jk\frac{2\pi}{N}n},n\in[0,N-1]\\ X_k=\sum_{n=}x[n]e^{-jk\frac{2\pi}{N}n},k\in[0,N-1]\\” eeimg=”1″> 　　
$\begin{bmatrix} X(0)\\ X(1)\\ \vdots\\ X(N-1) \end{bmatrix}= \begin{bmatrix} W_N^0 & W_N^0 & \dots & W_N^0\\ W_N^0 & W_N^{1\times1} & \dots & W_N^{(N-1)\times1}\\ \vdots & \vdots & \ddots & \vdots\\ W_N^0 & W_N^{1\times(N-1)} & \dots & W_N^{(N-1)\times(N-1)}\\ \end{bmatrix} \begin{bmatrix} x[0]\\ x[1]\\ \vdots\\ x[N-1] \end{bmatrix}$ 　　2. MATLAB内置的FFT函数　　输入长度为N的有限长序列x[n]，返回长度为n的象函数序列
$X(k\Omega),k=0,\dots,n-1$ 　　3. 四种傅里叶分析如何计算机实现？　　本文论述的基础是CTFT中时域与频域特征的对应关系：即时域采样间隔
T_s 对应于频域的频谱范围
f_s ；时域信号长度
对应于频域的谱线密度
$\omega$ ，两两互为倒数关系。用意是使用CTFT较清晰的物理意义来解释其他三种分析，为的是形成一种理解把握傅里叶分析的通俗的印象，因而从一开始就抛弃了严谨性，请读者注意。　　(一）DFS使用CTFT明确的物理意义来解释其他三种分析时域：离散周期（取主值），可以直接计算机处理；横坐标：
纵坐标：
$\bar{x}[n], n=1,...,N$ 频域：离散周期（取主值），便于在计算机中表示；横坐标：
$k\Omega_0=\frac{2k\pi}{N}\in[-\pi,\pi], k=1,... N$ 纵坐标：
实现：将DFT(FFT)获得的频谱密度除以信号周期N得到指数级数；　　（二）CFS时域：连续（致密的“采样”来近似“连续”）周期（取主值）；横坐标：
$t=nT_s, n=1,...,N=\frac{T_0}{T_s}\rightarrow\infty$ 纵坐标：
$\bar{x}(t), t\in[0,T_0]$ 频域：离散非周期（谱线密度/时域周期不变，谱线数增加，以刻画“非周期”）横坐标：
$k\omega_0 = \frac{2k\pi}{T_0}, k=0,1,2,...N\rightarrow\infty$ 纵坐标：
$c_k, k=0,1,2,...,N\rightarrow\infty$ 实现：在DFS基础上增大“采样频率”即可得到连续指数级数；　　（三）DTFT时域：离散非周期（增加有限长序列的长度刻画“非周期”）；横坐标：
$n=1,...,N\rightarrow\infty$ 纵坐标：
$x[n], n=1,...,N \rightarrow\infty$ 频域：连续（频域周期/时域采样频率不变，增加时域点数使频谱致密）周期（取主值）；横坐标：
$\Omega=\frac{2k\pi}{N}, k= -N/2,...,N/2-1$ 纵坐标：
$X(\Omega),\Omega\in [-\pi,\pi]$ 实现：DFT(FFT)可获得离散序列的频谱密度；　　（四）CTFT时域：连续非周期；致密“采样”来近似“连续”；增加时域离散点的个数刻画“非周期”;横坐标：
$t=nT_s, n=1,...,N=\frac{T}{T_s}\rightarrow\infty$ 纵坐标：
$\bar{x}(t), t\in[0,T\rightarrow\infty]$ 频域：连续非周期；增加时域点数使频谱致密，刻画“连续；”致密时域使频谱点数增加，刻画“非周期”；横坐标：
$\omega=\frac{2k\pi}{N}f_s,k=-N/2,\cdots,N/2-1$ 纵坐标：
$X(\omega), \omega\in[-f_s/2, f_s/2]$ 实现：在CFS获得的级数基础上乘以T，并对T取极限即可得到连续信号的频谱密度；　　小结　　 FFT是四种（傅里叶分析的内核运算，我们将变换理解为信息在时域和频域之间的交换，那么DFT/FFT则完成了这个过程中的数值计算，四种分析的差异则在于其输入输出的“接口”。　　一、DFS离散时间傅里叶级数　　
}X(k\Omega_0)e^{jk\Omega_0n},n\in[0,N-1]\\ X_k=\frac{1}{N}\sum_{n=}x[n]e^{-jk\Omega_0n},k\in[0,N-1]\\” eeimg=”1″>输入接口：对周期离散信号取主值从DFT到DFS：DFS公式在DFT公式基础上除以周期N
}x[n]e^{-jk\frac{2\pi}{N}n}\\ DFS:X(k\Omega_0)=\frac{1}{N}\sum_{n=}x[n]e^{-jk\Omega_0n}\\ 将转换后的指数形式频谱转换为三角形式\\ a_k=X_k+X_{-k}\sigusoftuad b_k=j(X_k-X_{-k})\quad 其中X_{-k}=X_k^*\\” eeimg=”1″>输出接口：将k转换为对应的
$k\Omega_0$ 需另外提供的参数：周期信号周期N 　　
$示例：x(t)=cos(2\pi t)+sin(6\pi t),采样周期f_{s2}=20Hz\\x[n]=cos(\frac{\pi n}{10})+sin(\frac{3\pi n}{10})时域间隔\frac{1}{f_{s2}},\ 时域周期T_0=1,\\如图周期频谱主值长度=对应样值周期N_0=f_{s2}T_0=20，k\Omega_0=\frac{\pi}{10}、\frac{3\pi}{10}\\$

图1. 离散周期序列、频谱幅度、频谱相角时域：离散周期序列频域（双边幅度谱）：离散周期序列（主值，长度为周期长度
N_0=20 ）　　二、CFS连续时间傅里叶级数　　
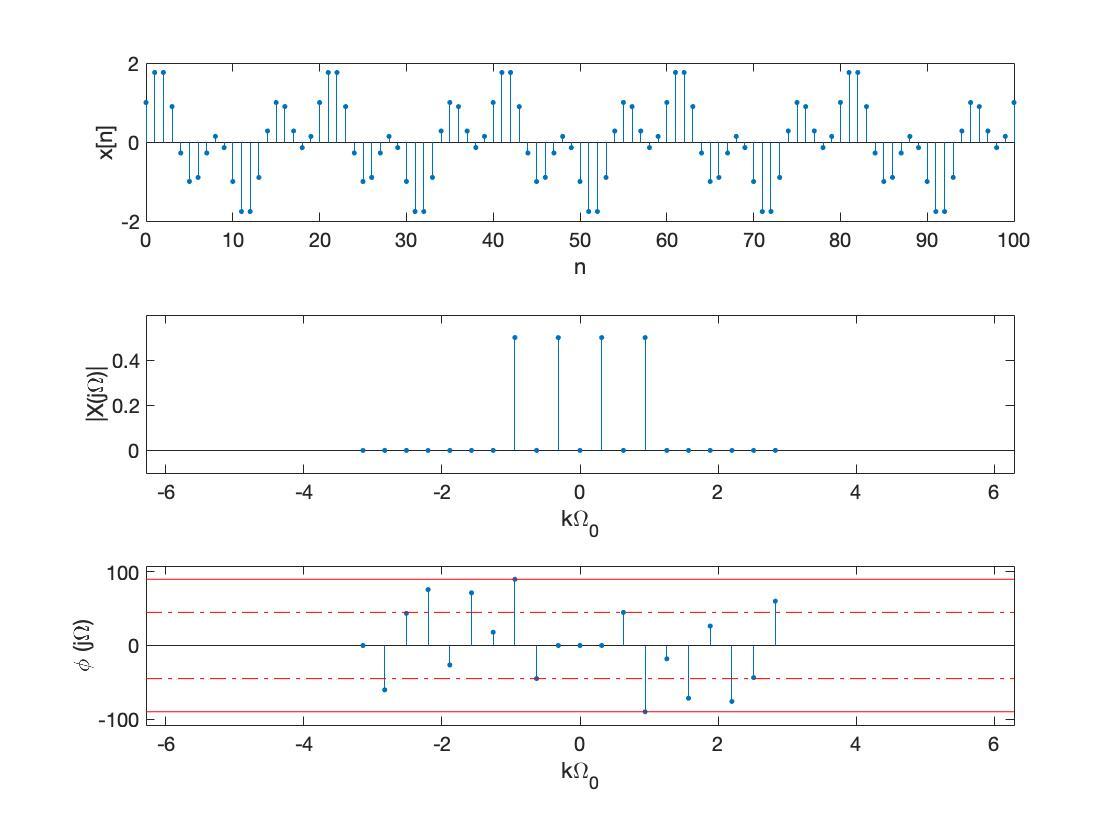
$指数频谱：c_k = \frac{1}{T}\int_T x(t)e^{-jk(\frac{2\pi}{T})t}dt,k\in(-\infty,\infty)\\ x(t)=\sum_{-\infty}^\infty c_k e^{jk(\frac{2\pi}{T})t},t\in[0,T]\\ 三角频谱：a_k = c_k+c_{-k}\sigusoftuad b_k = j(c_k-c_{-k})\\ x(t)=\sum_{N} a_kcos(k\omega t)+b_ksin(k\omega t)\\$ 输入接口：取周期函数主值从DFT到CFS：由上可得DFT到DFS的转换方法，令采样频率
$f_s\rightarrow\infty$ 时域：时间间隔
$\frac{1}{f_s}$ ，函数趋于连续频域：离散频谱周期
$2\pi f_s\rightarrow\infty$ ，刻画“非周期”输出接口：将转换后的指数双边频谱转换为三角单边频谱需另外提供的参数：周期信号周期
T_0 　　
$示例：x(t)=cos(2\pi t)+sin(6\pi t),时域周期T_0=1\\频谱离散、非周期,间隔为\frac{2\pi}{T_0}，如图分别对应\omega=2\pi、6\pi\\$

图2. 连续周期信号、双边频谱幅度、双边频谱相角、单边频谱级数时域：连续周期信号增大采样频率
f_s (连续性)，时域信号连续性增强，频谱长度增加(非周期性)频域（单边谱）：离散非周期序列　　三、DTFT离散时间傅里叶变换　　
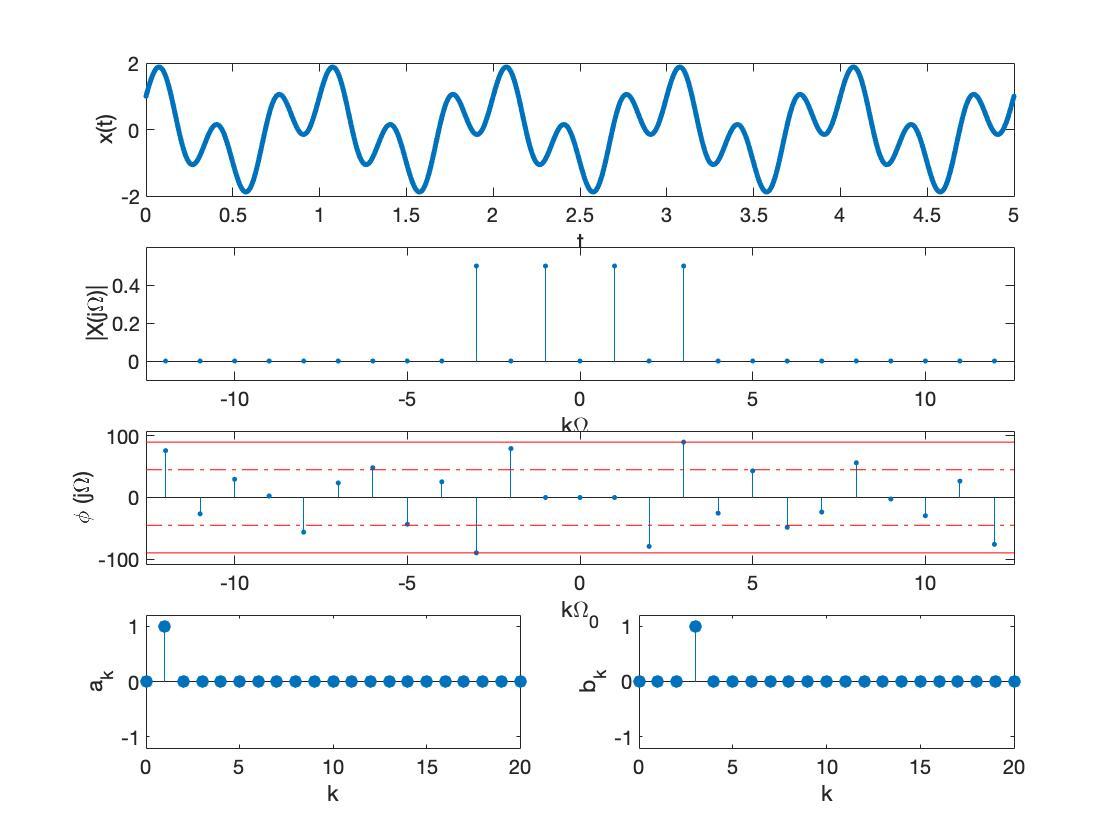
$x[n]=\frac{1}{2\pi}\int_{-\pi}^\pi X(\Omega)e^{j\Omega n}d\Omega,n\in(-\infty,\infty)\\ X(\Omega)=\sum_{n=-\infty}^{\infty}x[n]e^{-j\Omega n},\Omega\in[-\pi,\pi]\\$ 输入接口：无从DFT到DTFT：已知如何求周期函数的DFS 时域：周期 N取值远大于有限长信号长度 2N1(采样定理) 频域：
$F(k\Omega_0)=\lim_\limits{N\rightarrow\infty}Nc_k，c_k$ 为级数增加信号长度(非周期性)N可以使
$(-\pi,+\pi)$ 范围内频谱更密集(连续性)输出接口：将k转换为对应的
$\Omega=k\Omega_0=\frac{2\pi k}{N}$ ，其中
$N\rightarrow\infty$ 　　
N_1\end{cases}\rightarrow X(e^{j\Omega})=\frac{sin\Omega(N_1+1/2)}{sin(\Omega/2)}\\” eeimg=”1″>

图3. 离散非周期信号、实际测量频谱幅度、理论频谱幅度时域：离散非周期序列（有限长度）减小采样频率
f_s (离散性)，频谱主值长度减小(周期性) 增加时域长度(非周期性)，频谱密度增大（连续性）频域：连续周期信号（主值，长度为”采样频率”
$\Omega=2\pi$ ）　　四、CTFT连续时间傅里叶变换　　
$F(\omega)=\int_{-\infty}^\infty f(t)e^{-j\omega t}dt,\omega\in(-\infty,\infty)\\ f(t)=\int_{-\infty}^\infty F(\omega)e^{j\omega t}d\omega,t\in(-\infty,\infty)\\$ 输入接口：直接处理“致密采样”的时域信号从DFT到CTFT：已知如何求周期函数的CFS，时域：”周期”
T_0 取值远大于有限长信号长度
2T_1 ，即
$T_0\rightarrow\infty$ 频域:
$F(j\omega_k)=\lim_\limits{T\rightarrow\infty}Tc_k，c_k为级数$ 输出接口：为转换后的指数形式频谱提供一个频率的横坐标所需另外提供的参数：足够大的采样频率
f_s (时间信号的点距)：将t转换成为n=1，2，3 足够长的信号周期
T_0 (时间信号的持续时间)：以保证频带足够密集　　
$示例：x(t)=1(|t|<|T_1|)\rightarrow\frac{2sin(\omega T_1)}{\omega}\\$

图4. 连续非周期信号、实际测量频谱幅度、理论频谱幅度时域：连续非周期信号增大采样频率
f_s (连续性)，时域信号连续性增强，频谱长度增加(非周期性)增加时域长度(非周期性)，频谱密度增大（连续性）频域：连续非周期频谱，带宽
$B_f=\frac{2\pi}{T_1}=2\pi$ 　　个人实验，欢迎批评指正

用fft算法分析频谱_FFT频谱分析

相关推荐