二叉排序树构造唯一吗_二叉排序树时间复杂度

一文带你搞定【二叉树】 　　1. 树的名词与概念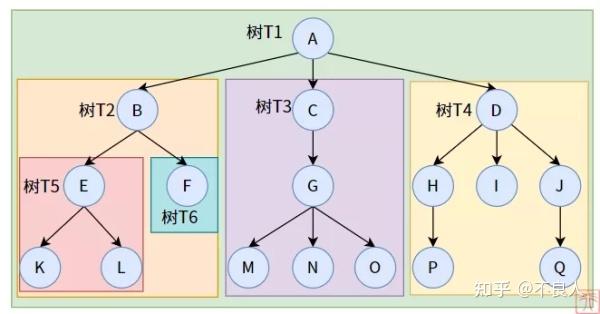 　　

子树：树是一个有限集合，子树则是该集合的子集。就像套娃一样，一棵树下面还包含着其子树。比如，树T1 的子树为 树T2、T3、T4，树T2的子树为 T5、T6 。 上图中还有许多子树没有标记出来 。结点(Node)：一个结点包括一个数据素和若干指向其子树分支。比如，在树T1 中，结点A 包括一个数据素A 和 三个指向其子树的分支。上图中共有 17 个结点 。根结点(Root)：一颗树只有一个树根，这是常识。在数据结构中,“树根”即根节点。比如，结点A 是树 T1 的根结点; 结点C 是树T1 的子结点，是树 T3 的根结点。度(Degree)：一个结点拥有的子树数。比如，结点A 的度为 3，结点G 的度为 3，结点H 的度为 1。叶子(Leaf)/ 终端结点：度为 0 的结点被称为叶子结点，很形象吧。比如，对于树 T1来说，结点F、I、K、L、M、N、O、P、Q 均为叶子节点。分支结点 / 非终端结点：和叶子结点相对，即度不为 0 的结点。内部结点：顾名思义，在树内部的结点，即不是根结点和叶子结点的结点。双亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点； 如上图：A是B的父节点孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点； 如上图：B是A的孩子节点兄弟节点：具有相同父节点的节点互称为兄弟节点； 如上图：B、C是兄弟节点堂兄弟节点：双亲在同一层的节点互为堂兄弟节点；如上图：E、G、H互为堂兄弟节点节点的祖先：从根到该节点所经分支上的所有节点；如上图：A是所有节点的祖先子孙：以某节点为根的子树中任一节点都称为该节点的子孙。如上图：所有节点都是A的子孙层次(Level)：从根结点开始，根为第一层，根的孩子为第二层，依次往下。比如，结点K 在树 T1 中的层次为 4。深度(Depth)/ 高度：指树的最大层次。比如，树 T1 的高度为 4 。有序树: 树中任意节点的子结点之间有顺序关系，这种树称为有序树 。无序树 : 树中任意节点的子结点之间没有顺序关系，这种树称为无序树,也称为自由树 。森林：由m（m≥0）棵互不相交的树构成一片森林。如果把一棵非空的树的根节点删除，则该树就变成了一片森林，森林中的树由原来根节点的各棵子树构成 。 　　2. 什么是二叉树 　　满足以下两个条件的树称之为二叉树：本质上为有序树；每个结点的度不能超过2，即结点的度仅能为0，1，2。 　　3. 二叉树的性质 　　二叉树中，第 i 层最多有
个结点。如果二叉树的深度为 K，那么此二叉树最多有
-1 个结点。二叉树中，终端结点数（叶子结点数）为 n0，度为 2 的结点数为 n2，则 n0=n2+1。具有n个节点的满二叉树深为
。性质 3 的计算方法为：对于一个二叉树来说，除了度为 0 的叶子结点和度为 2 的结点，剩下的就是度为 1 的结点（设节点数为 n1），那么总结点数 n=n0+n1+n2。同时，对于每一个结点来说都是由其父结点分支表示的，假设树中分枝数为 B，那么总结点数 n=B+1。而分枝数是可以通过 n1和 n2表示的，即 B=n1+2*n2。所以，n 用另外一种方式表示为 n=n1+2*n2+1。两种方式得到的 n 值组成一个方程组，就可以得出 n0=n2+1。 　　4. 二叉树的分类 　　4.1 满二叉树 　　如果二叉树中除了叶子结点，每个结点的度都为 2，则此二叉树称为满二叉树。

满二叉树示意图 　　满二叉树除了满足普通二叉树的性质，还具有以下性质：满二叉树中第 i 层的节点数为
个。深度为 k 的满二叉树必有
-1 个节点 ，叶子节点数为
。满二叉树中不存在度为 1 的节点，每一个分支点中都两棵深度相同的子树，且叶子节点都在最底层。具有 n 个节点的满二叉树的深度为
。 　　4.2 完全二叉树 　　如果二叉树中除去最后一层节点为满二叉树，且最后一层的结点依次从左到右分布，则此二叉树被称为完全二叉树。

　　完全二叉树除了满足普通二叉树的性质外，还满足以下性质： n个结点的完全二叉树的深度为⌊log2n⌋+1; （注：⌊ ⌋表示向下取整） 对于任意一个完全二叉树来说，如果将含有的结点按照层次从左到右依次标号，对于任意一个结点 i ，完全二叉树还有以下几个结论成立： 　　1). 当 i >1 时，父结点为结点 ⌊i/2⌋ 。（i=1 时，表示的是根结点，无父结点） 　　2). 如果 2*i>n（总结点的个数） ，则结点 i 肯定没有左孩子（左叶子结点）；否则其左孩子是结点 2*i 。 　　3). 如果 2*i+1>n ，则结点 i 肯定没有右孩子；否则右孩子是结点 2*i+1 。 　　4.3 二叉搜索树（又称: 二叉排序树、二叉查找树） 　　

　　二叉搜索树：可以为空树，或者是具备如下性质： 　　A. 若任意节点的左子树不空，则左子树上所有节点的值均小于它的根节点的值； 　　B. 若任意节点的右子树不空，则右子树上所有节点的值均大于它的根节点的值； 　　C. 任意节点的左、右子树也分别为二叉搜索树; 　　还有一种特殊情况：

　　这种情况下，二叉搜索树已经变更为链表，搜索一个素的时间复杂度从O(
)退化为O(n), 出现这种情况的原因是二叉搜索树没有自平衡的机制，所以就有了平衡二叉树。 　　4.4 平衡二叉树 　　

　　平衡二叉树是一种二叉排序树，其中每个结点的左子树和右子树的高度差至多等于1。它是二叉排序树的一个进化体，它有几种实现方式：、 平衡因子：平衡二叉树是在二叉查找树的基础上进行构建，为了维持平衡二叉树的平衡，那么就需要一种机制来判断平衡二叉树是否是平衡的。这种机制就叫做平衡因子。平衡二叉树上某个结点的左子树深度减去右子树深度的值，就称为此结点的平衡因子。最小不平衡树：距离插入结点最近的，且平衡因子的绝对值大于1的结点为根的子树，称为最小不平衡树。 　　平衡二叉树特点:平衡二叉树是一种二叉查找树每个结点的左子树的高度减去右子树的高度的绝对值不超过1空树和左右子树都是平衡二叉树相比红黑树，平衡二叉树比较适用于没有删除的情况 　　什么是左旋？ 　　左旋：指将根节点的右侧往左拉，原先的右子节点变成新的父节点，并把多余的左子节点出让，给已经降级的根节点当右子节点

　　什么是右旋？ 　　右旋：指将根节点的左侧往右拉，原先的左子节点变成新的父节点，并把多余的右子节点出让，给已经降级的根节点当左子节点

　　失衡 ：当我们在一个平衡二叉树上插入一个结点时，有可能会导致失衡，即出现平衡因子绝对值大于 1 的结点，如下图，当插入结点后，其中key为53的结点失去了平衡，我们称该结点为失衡结点，我们必须重新调整树的结构，使之恢复平衡

　　不一定只有一个结点失去平衡，有可能插入一个结点会让多个结点失衡。这时候找最小的失衡子树的根节点作为失衡结点。 　　恢复平衡 ： 那如何去恢复平衡，使得二叉搜索树依然成立为一棵平衡树？先来看平衡调整的四种类型：

　　举个例子：如第一个，当平衡二叉树为AB时，插入一个C结点，使得失衡了，失衡结点为A，此时因为C结点插入的位置为失衡结点的左孩子的左孩子，所以是LL型，以此类推。 　　为了恢复平衡，针对每一种都不一样，但目的都是调整为平衡的，且不能违背二叉搜索树的性质：如下图是每种失衡类型的解决方法，每个都不太一样，目的都是一样的，把key的值为中等的变为树的根，最小的放在左孩子，做大的放右孩子，通过这一目的，降低树的高度，也不用死记硬背。

　　这一操作被称为树的旋转，如LL型被称为右旋，RR型称为左旋，LR型是先左旋，再右旋，RL型先右旋再左旋。 　　4.5 AVL树 　　AVL树是根据它的发明者G.M.Adelson-Velsky和E.M.Landis命名的。它是最先发明的自平衡二叉查找树，也被称为高度平衡树。

　　AVL树本质上还是一棵二叉搜索树，它的特点是：本身首先是一棵二叉搜索树。带有平衡条件：每个结点的左右子树的高度之差的绝对值（平衡因子）最多为1。也就是说，AVL树，本质上是带了平衡功能的二叉查找树（二叉排序树，二叉搜索树）。 　　如果在AVL树中插入或删除节点后，使得高度之差大于1。此时，AVL树的平衡状态就被破坏，它就不再是一棵二叉树；为了让它重新维持在一个平衡状态，就需要对其进行旋转处理。实现平衡的关键在于旋转操作。 　　4.6 红黑树 　　红黑树，是一种二叉搜索树，但在每个结点上增加一个存储位表示结点的颜色，可以是Red或Black。 通过任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径会比其他路径长出俩倍，因而是接近平衡的。因而，红黑树是相对接近平衡的二叉树，并不是一个完美平衡二叉查找树

　　红黑树的性质：结点不是红色就是黑色根节点是黑色的每个红色结点的两个子结点都是黑色。（从每个叶子到根的所有路径上不能有两个连续的红色结点）从任一结点到其每个叶子的所有路径都包含相同数目的黑色结点每个叶子结点都是黑色的(叶结点即指树尾端NIL指针或NULL结点) 　　红黑树与AVL树的比较 ： 　　红黑树和AVL树都是高效的平衡二叉树，增删改查的时间复杂度都是O(
)，红黑树不追求绝对平衡，只需保证最长路径不超过最短路径的2倍，相对而言，降低了插入和旋转的次数，所以在经常进行增删的结构中性能比AVL树更优，而且红黑树实现比较简单，所以实际运用中红黑树更多。 　　5. 二叉树的存储结构 　　二叉树一般可以使用两种结构存储，一种顺序结构，一种链式结构。 　　5.1 顺序存储 　　顺序结构存储就是使用数组来存储，一般使用数组只适合表示完全二叉树，因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储 。 　　对于完全二叉树的存储，仅需对其从根节点开始仅需编号，使用数组存储编号即可。取出式依据完全二叉树由左到右分布的性质恢复即可。

　　5.2 链式存储 　　二叉树的链式存储结构是指，用链表来表示一棵二叉树，即用链来指示素的逻辑关系。 通常的方法是链表中每个结点由三个域组成，数据域和左右指针域，左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。





　　6. 二叉树的构建 　　在进行前序，中序和后序遍历代码编写之前，我们需要先构建出一颗二叉树，不妨我们就以下面的二叉树为例，把其构建出来，在下图中已给出三种遍历结果。如果我们利用中序遍历去构建的话，构建完C B节点后就去构建E节点就找不到关系了，所以行不通，如果我们利用后序遍历去构建的话，构建完C节点，再去构建E结点就找不到关系了 ，所以也行不通，最后我们把希望寄托在了前序遍历上。(不懂前序，中序，后序遍历的可以先去看下后面的遍历部分的相关概念)

　　利用前序遍历去构建这颗二叉树，构建完A节点，A的左孩子不为null，再构建B节点，B的左孩子不为null，再构建C节点，C的左孩子为null，然后去构建其右孩子，右孩子也为null，此时以C节点为根节点的子树构建完毕，再去构建B的右孩子D结点… 　　所以我们可以根据前序遍历的结果给出这样一个数组 ABC##DE##F##G#H##（null用#表示，当遇到#时返回null）。 　　首先给出一个节点类： 　　利用数组创建二叉树： 　　测试： 　　7. 二叉树的遍历 　　所谓遍历(Traversal)是指沿着某条搜索路线，依次对树中每个结点均做一次且仅做一次访问。二叉树是一种重要的数据结构，其遍历方式分为：深度遍历和广度遍历，深度遍历有前序、中序以及后序三种遍历方法，广度遍历即层序遍历。 　　7.1 前序遍历(又称 : 先根遍历) 　　前序遍历的思想是：（根左右） 　　二叉树的前序遍历的枚举规则为：根结点 —> 左子树 —> 右子树，也就是给定一棵树，输出操作当前节点，然后枚举左子树(左子树依然按照根左右的顺序进行)，最后枚举右子树(右子树也按照根左右的顺序进行)，这样得到的一个枚举序列就是二叉树的前序遍历序列(也叫先序 , 先根)。 　　前序遍历在二叉树树的顺序可以看下图(红色箭头指向的表示需要访问的，可以看出从父节点枚举下来第一次就要被访问)。

　　在具体实现的方式上，有递归方式和非递归方式两种实现方式。 　　首先我们先把上面的树创建出来： 　　递归实现 : 　　非递归实现 : 　　算法思想：将遍历树的指针指向根节点，并将根节点入栈，判断栈是否为空，如果不为空，将栈顶素出栈，并判断该节点的右子树是否为空，如果不为空，入栈，再判断其左子树是否为空，若不为空，入栈，循环以上步骤，直至栈为空。 　　7.2 中序遍历(又称: 中根遍历) 　　中序遍历的思路是：（左根右） 　　遇到一个节点，先缓存，看其是否有左子节点，若有，则输出左节点，再输出原节点，最后输出右节点。中序遍历在二叉树的顺序可以看下图(红色箭头指向的表示需要访问的，可以看出如果子树为null，那肯定要访问，否则就是从左子树回来的时候才访问这个节点)。

　　递归实现 : 　　非递归实现 : 　　算法思想：将二叉树的根节点赋值给要进行遍历的指针，用该指针进行遍历，若当前节点非空，则将该节点进行入栈操作并访问其左子树，循环执行，直到当前节点为空时，让栈顶的素出栈，然后访问其右子树，再重复如上操作，直到指针指向空并且栈为null时退出循环。 　　7.3 后序遍历(后根遍历) 　　后序遍历的思路是：（左右根） 　　遇到一个节点，先缓存，看它是否存在左子节点，有则输出，接着看其是否有右子结点，最后输出原节点。后序遍历在二叉树的顺序可以看下图(红色箭头指向的表示需要访问的，可以看出如果子树为null，那肯定要访问，否则就是从右子树回来的时候才访问这个节点)。

　　递归实现 ： 　　非递归实现 : 　　算法思想：将二叉树的根节点赋值给要进行遍历的指针ptr，用该指针进行遍历，若当前节点非空，则将该节点进行入栈操作并访问其左子树，循环执行，直到当前节点为空时，让栈顶的素出栈，判断其右子树是否为空且是否遍历，如果非空且未遍历该右子树，再将其压入栈中并遍历其右子树；如果为空或已遍历则访问该节点并弹出栈，同时设置标记指针pre记录该节点（用于判断节点的右子树是否已经遍历），再将遍历的指针ptr置为空，下次遍历直接取出栈顶素，直至遍历的指针为空且栈为空时退出循环。 　　7.4 层序遍历 　　按照二叉树的层次从上至下从左至右进行遍历。 　　算法思想：准备一个队列：将根节点入队，访问其队头素，判断该节点的左右孩子是否为空，不为空则入队，循环直至队列为空结束。

　　代码实现： 　　7.5 S形层序遍历 　　除了这个直接层序遍历，二叉树还有很高频的就是S形遍历

　　算法思想 : 观察S形遍历的结果我们发现，
，所以我们准备两个栈进行操作，首先将根节点入栈1，然后判断栈1是否为空，显然不为空，那么将栈顶素出栈，判断其左孩子是否未空，不为空如栈2，其右孩子是否为空，不为空如栈2，当栈1为空时，退出此循环操作；再判断栈2是否为空，不为空，将栈顶素出栈，判断其右孩子是否为空，不为空如栈1，判断左孩子是否为空，不为空如栈1，当栈2为空时，退出此循环操作；当栈1和栈2同时为空时，退出程序。 　　代码实现：