相机也成双——直观理解对极几何中的四个重要矩阵（外参矩阵、内参矩阵、基本矩阵、本质矩阵） 本文最早发表于CSDN平台：CSDN@祁医生不是一只好程序猿 引言 在奔逸不羁的童年，笔者对理科知识的好奇无际无边。某天曾在外婆家的煤棚子里一通乱翻，缴获了大舅学生时代的几何光学课本，不料遭遇开幕雷击： “人的眼球好比照相机，我们要为革命而保护视力！” 对于一个孩童干瘪的脑袋来说，实在是难以领悟眼球和相机有何关联，也就更别提它们如何跟革命扯到一起了。时隔多年，笔者当物理学家的童年梦想未果，而是成为了一名脑外科医生。有了医学专业背景再回想，觉得书上这话讲得还算不孬——两只眼球属实如同两枚相机，乖巧而警觉地伏于眶窝内，可调光轴（眼外肌），可调焦距（睫状体）、可调光圈（瞳孔），既有底片（视网膜），又有电缆（视神经），最后把照片发给主机（大脑）。大脑整合双眼图像，分析差异，计算出物体到眼球的距离与深度。这些信息加上日积月累的视觉经验，便造就了双目立体视觉，使人看到立体的世界。 归纳逻辑推理告诉我们：欲谋取对事物的完整理解，要把问题一般化，还要把问题特殊化。上一段文字从眼球与相机的关系中抽象出了双目立体视觉的概念，是问题一般化。而问题特殊化是反向过程，即从双目立体视觉的概念反观眼球与相机的比喻，便可总结事物的关键部分和次要部分，专注于分析与科学问题关联最大的因素。 场景的简化版显而易见——空间中有一物体，双眼正注视着这个物体，产生两幅图像。大脑分析处理两幅图像，造就了双目立体视觉。前人正是通过双眼看世间万物这个模型，抽象出了对极几何的数学概念。本文从眼球-相机的比喻出发，聊聊笔者对对极几何中的四个重要矩阵，即外参矩阵、内参矩阵、基本矩阵和本质矩阵的直观理解。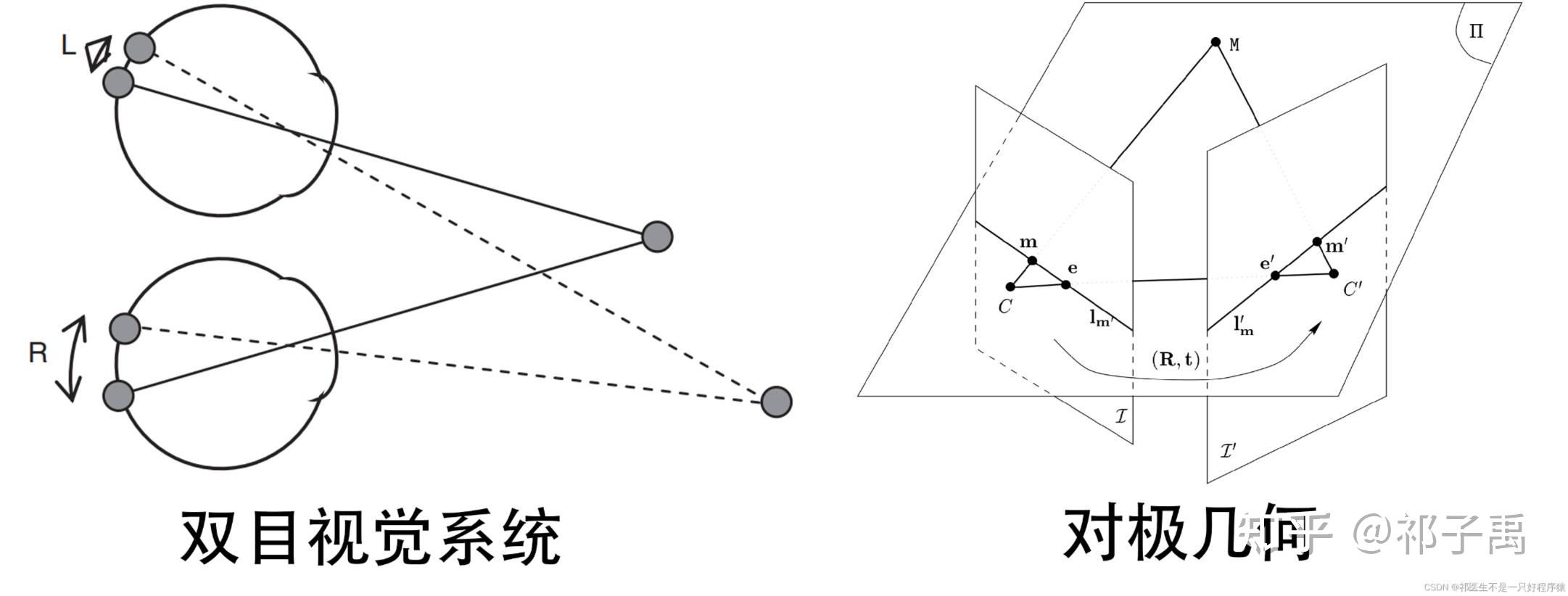 
注：左图引自Read, J. C. (2015). Stereo vision and strabismus. Eye, 29(2), 214-224. 右图引自Zhang, Z. (1998). Determining the epipolar geometry and its uncertainty: A review. International journal of computer vision, 27, 161-195. 1. 外参矩阵（Extrinsic Matrix） 在真实世界中，物体有它的绝对位置和朝向——它的经纬度坐标，是面朝南还是面朝北。而在人眼中，该物体也有它的相对位置和朝向——它距离眼球多远，是面向人还是背朝人，正如诗所云“横看成岭侧成峰”。 物体的位姿从人的单眼变换到世界，就是外参矩阵所代表的变换。因此，左眼有左眼的外参矩阵，右眼有右眼的外参矩阵。 当物体相对于人眼发生线性变换时，外参矩阵随之改变。线性变换可以是平移（行驶的汽车），可以是旋转（转动的陀螺），可以是放缩（萎泄的皮球），也可以是仿射（斜阳之下的树影）。 术语总结：外参矩阵定义了相机坐标系和世界坐标系的关系，它是从相机坐标系转换到世界坐标系的变换矩阵。 2. 内参矩阵（Intrinsic Matrix） 外参矩阵描述了从世界到眼球的变换，内参矩阵则描述了从眼球到视网膜的变换。 眼球坐标系中的物体是三维的，而视网膜上的（实）像是二维的，因此，内参矩阵是一种从三维到二维的投影变换。投影变换的基本原理是：光在均匀透明的介质中沿直线传播。这也是几何光学体系的基本假设。因此，只要同时控制光源的位置、光的方向及其传播介质恒定不变，那么光路一定是确定的，实像的位置和大小将仅仅取决于光屏的位置和方向。 返回眼球的举例上来，只要使物体的位姿恒定，使人眼的位姿也恒定，那么这只眼球所看到的画面将永远是同一张画面。换言之，一个物体在一只眼球中有且只有一个确定的实像。 所以，每只眼球都必然存在唯一确定的变换矩阵，它使得物体与实像能够一一对应。这个矩阵就是内参矩阵，它反映了眼球的固有折光参数，因此又称“固有参数矩阵” 然而，不同人眼球不同，有人近视，有人远视，有人散光，有人斜视。所以，即便让他们的眼球都在同一位置观察同一物体，所看到的画面也很可能不同——正常人看到的清晰的物体，近视和远视的人说模糊，散光的人说有变形，斜视的人觉得歪曲，晶体被摘除的人说呜呜呜你们在说什么我怎么听不懂啊？换言之，不同眼球的内参矩阵不尽相同，内参矩阵取决于眼球的视轴、折光率、前后径等固有参数。 术语总结：内参矩阵定义了相机的内部参数，它记录了焦距、主点偏移等参数。对于定焦相机而言，内参矩阵是恒定的，在相机标定过程中需要求出。 3. 基本矩阵（Fundamental Matrix） 外参矩阵和内参矩阵概念，都以单只眼球举例，最初也都来源于位于单目视觉的范畴。前文提到双目立体视觉的基础是：大脑可以分析左右眼看到同一物体有何差异。而描述左目图像和右目图像之间变换关系的，就是基本矩阵。 这种变换关系是线性的吗？答案是肯定的。从物体到左目图像发生了线性变换，从物体到右目图像也发生了线性变换，那么，物体、左目图像与右目图像必然能在同一线性空间中描述，从左像到右像的变换也显然是线性变换。 变换是线性的，也就意味着点在左右图片中是一对一的映射，绝不会存在左图中有一个点对应着右图中的两个点。否则就会出现荒谬至极的情况——一个土豆摆在一个视力正常的人面前，他左眼看到一个土豆，右眼却看到了两个土豆。 因此，基本矩阵反映了左右视网膜上图像中的点的对应关系，这种关系可以通过几组对应点的位置，构成线性方程组来求解。 与内参矩阵的情形相似，不同人双眼的基本矩阵也不同，双目的距离（瞳距）就是一个典型的影响因素。精于推理的读者朋友可能马上会有以下疑问：是不是瞳距越大的人，感受视差的能力越强，立体感越好？笔者作为脑外科医生并不清楚，实难回答。那么，拥有眼科专业背景的读者朋友们，你们怎么看？欢迎在下方评论区留言赐教！ 术语总结：基本矩阵关系了左目图像和右目图像中对应点的关系，可以用于确定双目相机系统的几何结构，以及确定视差。 4. 本质矩阵（Essential Matrix） 除瞳距外，人们在双眼焦距、光轴、折光性上的差异也会影像左目图像与右目图像的差异。凝练来说，基本矩阵除了受到双眼几何关系制约，还受到眼球固有参数的影响。本质矩阵是在基本矩阵的基础上，排除眼球固有参数的影响，而仅仅保留双眼的几何关系。正是基于这个推理，本质矩阵可以通过基本矩阵和内参矩阵求得。 如果说基本矩阵反映的是左目图像与右目图像的变换，那么本质矩阵反映的则是左眼球与右眼球的变换。将眼球位置和姿态简化为一个有朝向的质点，那么从左质点到右质点位姿的变换，正是本质矩阵所表征的。 前文多次提到斜视，那么什么是斜视呢？如果视力正常者的双眼去追踪一个运动物体，那么他两只眼球的联合转动理应协调一致。假如一些病理性因素（如眼肌损伤、眼球畸形、眶内炎症、颌面骨折等）会破坏这种联合运动的协调性，就会形成视觉障碍，斜视患者不得不通过歪斜的眼位来补偿这种不一致。在临床上，眼科医师们为斜视患者实施的矫正手术，也正是修复了患者左右眼之间的“本质矩阵”，从而使这个矩阵在追踪物体时总是协调一致，流转自如。 术语总结：本质矩阵是基本矩阵和内参矩阵的函数，它记录了两个相机坐标系的相对关系。本质矩阵可以用于计算相机的位姿，以及三维点的深度。 总而言之，外参矩阵、内参矩阵、基本矩阵、本质矩阵总是相互关联的，无论是在单目系统还是在双目系统，无论是从物体到眼球，还是从眼球到视觉图像。 写在最后 基础科学如数学，常常从抽象走向另一个抽象，而应用科学如工学，却是于抽象与具体间“其中往来种作”。众多科普文章则是通过创造性的诠释与表现，将科学知识呈现得更加生动、直观、有趣，避免理论被复杂的抽象所架空，最终疏远大众与科学的距离。本文乃笔者一己之思，全文无一公式，仅供读者朋友们参考，若能抛砖引玉，甚至使“黄发垂髫并怡然自乐”，实乃笔者之幸！ ———————————————— 版权声明：本文为CSDN博主「祁医生不是一只好程序猿」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。 原文链接：【情人节特辑】相机也成双–直观理解对极几何中的四个重要矩阵（外参矩阵、内参矩阵、基本矩阵、本质矩阵）_内参矩阵是什么_祁医生不是一只好程序猿的博客-CSDN博客
2024最新激活全家桶教程，稳定运行到2099年，请移步至置顶文章：https://sigusoft.com/99576.html
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请联系我们举报，一经查实，本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处：https://sigusoft.com/65291.html
