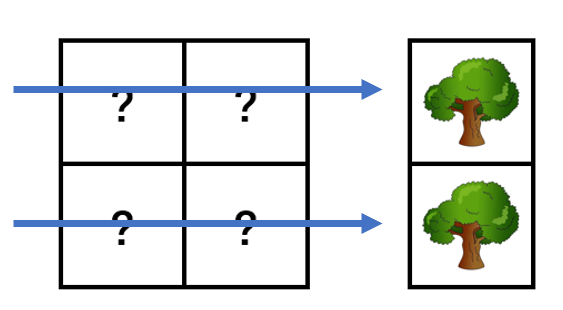
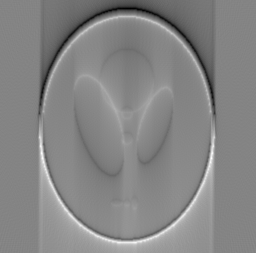
医学图像重建算法综述（CT） 医学图像重建算法综述 写在前面： 2020年上半年疫情期间，于家中闭关修炼，功力大涨，此乃一项。为广大初学者分享. 知乎上传word不能自动转换公式，想要原稿的私聊我，加我好友，发你原稿 摘要： 随着计算机技术的不断发展，医学成像技术越发成熟，图像重建算法在临床及产业应用中的地位越发突出。本文围绕医学断层成像重建算法，从断层成像的基本概念讲起，一直到平行束反投影重建算法和迭代重建算法，包括直接反投影算法、滤波反投影算法、卷积反投影算法、微分-希尔伯特反投影算法、梯度下降算法、ML-EM迭代重建算法等常见方法。系统论述并推导了多种基础的断层成像算法，通过深入浅出的方式解释这些算法的原理，并配有许多生动的图像辅以说明。为增强实践性，几乎对每一种算法都编写了基于MATLAB平台的演示程序，成果复现性强。本文还涵盖了更深一步的图像重建技术，如使用截断数据进行ROI重建。 关键词：医学重建算法;平行束反投影成像;迭代算法;医学成像技术 断层成像的基本概念 1.1 断层成像 一谈到医学成像，断层成像是其中相当重要的部分。所谓断层成像，就是要得到一个物体内部的截面图像。 如果你想知道一个西瓜的内部构造，比较方便的做法是：用刀将西瓜切开（图1.1）。但若将这个办法用在病人身上绝非明智之举。人们绞尽脑汁，希望找到一种不用把物体切开，便能其内部截面信息的方法，这种方法就是断层成像。 
图1.1：把西瓜切开，截面清清楚楚 断层成像实质上就是一种分析数据的手段。现在，几乎所有自然科学的工作都绕不开数据分析（Data Analysis）。通常来讲，数据分析包含两个目的：1. 从实际的物理现象当中通过某种技术手段，一系列参数；2. 确保这些参数可以较好地重建现实中的物理现象。这里使用了“较好地”而非“完整地”来修饰人们希望达到的重建程度，是因为现实世界客观存在着种种环境限制，不可避免地为测量引入噪音。同时，由于人类电子产业发展的局限性，所有连续的自然现象在计算机中都是以“插值”的方式进行存储与处理的。插值的存在势必会带来非测量误差，在之后的内容中本文将阐述历史上的学者们为了征服“插值”带来的影响做了哪些努力。 总之，想要在不切开西瓜的前提下完美重建内部影像是一件几乎不可能的工作。但通过算法可以将诸般影响降到最低。本文所罗列出的图像重建算法是经典与基础的，并不涉及现代机器学习技术。 下面通过一个简单的小案例来引入断层成像技术的基本概念。 案例1：公园里的树 假设一日冷空淡碧，天色绝好，A同学到人民公园游玩。可惜公园正值修缮，不得入内，郁郁不得的A只好在公园外拍摄几张照片返回。回到家之后，A同学整理照片时心念一动：可不可以通过照片归纳出人民公园里树木的位置呢？他当即开始了尝试。我们假设公园为一个2×2的方阵，方阵的每一个素表示坐标，每一个坐标至多只有一棵树（图1.2）。 
图1.2：公园轮廓 现在有两幅照片，分别从公园的南侧与东侧拍摄，它们是这样的（图1.3，图1.4）： 
图1.3：从东侧拍公园 图1.4：从南侧拍公园 现在，我们再假定一个条件：这个公园中，每一行与每一列最多只有一棵树。那么，综合上述条件，能否复原出现实世界中公园里树的分布呢？ A同学列了四个方程：
尝试解方程后，他认为不行，因为他发现有两种分布符合上述条件（图1.5，图1.6）。 
图1.5：分布一 图1.6：分布二 那么，A同学现在如何确定公园中树的分布呢？答案很简单：再拍一张照片，就能将两种可能的分布缩减为一种。它的拍摄角度是这样的（图1.7）： 
图1.7：新的拍摄角度 CT的成像过程与上述过程相似，都是将平面信息投影在多个投影面上，再通过归纳与计算这些投影面的信息，反推出人体中真实的物质分布，两者最大的区别就是：CT成像中每一个单格没有规定最多只有一棵树，而是表示一个“衰减系数”。就像刚刚解方程的过程一样，有时候方程组是解不出来唯一解的，或者说方程矩阵是非满秩的。这是因为我们收集到的数据不够多，因此CT需要切换多个角度，多个投影面的信息，就像A同学后来做的工作一样。巧妇难为无米之炊，如果的数据不够多，再强大的算法也无法复原出原始图像。 在这里要提出的是，现实情况下，即使手上有足够多的数据（方程），通常也解不出来这个方程组。这是因为X光照射过程不可避免地引入噪声干扰，方程矩阵往往是“不相容的”。我们只能获得近似解而不是精确解。同时，解方程的过程实在太慢了，尤其是拍摄角度多起来后，将极大地影响成像速度。现在多使用反投影的手段重建CT影像。 1.2投影 对二维平面(x-y)密度函数的投影实际上是一个求线积分的过程。该过程被人们称作“拉东变换（Radon Transform）”。它的数学表述如下：
（1-1） 这里引入了一个狄拉克函数，该函数用来限制投影过程必须按照一条投影线与一定的投影角度进行。狄拉克函数是一个广义函数，亦可理解为一种分布，在这里简单说明狄拉克函数的性质：
相信根据这两条定义，不难想象出一个在非零处处处为零，在零处具有无限高度的函数。因此，狄拉克函数非常适用于筛选某一条件的数值。 投影首先要找到一个旋转中心，接着基于这个中心，使用旋转角度θ与投影线距旋转中心距离s建立投影函数。（图1.8） 
图1.8：对x-y平面上的均匀圆盘函数的投影。曾更生，《医学图像处理》 下面的一个例子考虑y轴上的一个点源，请留意探测器上点源留下的足迹s的位置，该点源在探测器s的位置产生了一个脉冲，该脉冲的位置可以表示为。
位置s是探测器旋转角度θ的正弦函数。这也是为什么我们获得的投影图像往往是多个正弦函数的叠加（图1.9）。 
图1.9：投影位置s是探测器旋转角度θ的正弦函数 下面一个例子让我们回到之前的2×2矩阵。探测器是离散的，它由四个离散的探测单组成，这个2×2矩阵是个连续的图像，每个矩阵素代表一个均匀的像素。像素的数值 (=1, 2, 3, 4) 为第个像素的线密度数值。这个矩阵图像的投影数据是图像线积分数值，为探测器旋转角（图1.10）。这个线积分的“线” 在每个像素内的线段长度记为，下标是探测的编号，下标是像素的编号。如果第条线与第个像素不相交，则=0。这样一来，投影值可用如下表达式给出：
图1.10：投影值实际上是像素值的加权和，权函数是“线”在像素内的线段长度 二、平行束重建算法 2.1中心切片定理 中心切片定理是断层成像的理论基础，它给予人们信心：从数学上证明了，根据投影值是完全可以重建原始图像的。 二维图像的中心切片定理表述为：密度函数
的投影函数 的傅里叶变换 等于函数 的傅里叶变换 沿探测器平行方向过原点的片段。（图2.1，图2.2） 
图2.1：二维中心切片定理的直观形象 
图2.2：二维中心切片定理的说明图 如果探测器围绕物体旋转至少180度，那么物体的二维傅里叶变换 就可以通过探测器探测到的 覆盖整个空间。接下来只需进行简单的二维逆傅里叶变换即可将 恢复为 。 下面是基于matlab环境下的一个进行二维中心切片定理的应用。所处理的图片是matlab自带的一个名为“phantom（幻影）”的图片（图2.3），人们常常用它来测试自己的重建算法。 
图2.3：phantom 在这个例子中将展示我们是如何将phantom转换到二维频域的，又如何从频域重建的。（图2.4） 
图2.4：左：重建后的图像 右：根据中心切片定理拼凑出的频率域 该程序将投影角度从0°到179°均分为180份，即构建了180个拉东变换向量，再将这些向量分别进行傅里叶变换变换到频率域去，最后将180个这样的切片在原函数频率域上叠加，就完成了二维的中心切片定理应用。 下面从数学角度证明中心切片定理： 中心切片定理可表述为： （2-1） 证明： 首先给出一维傅里叶变换公式：
（2-2） 将式1-1
代入
交换积分次序，得
(2-3) 根据狄拉克函数性质，可以再作如下变换
(2-4) 将（2-4）代入式（2-3）中，便可得到
（2-5） 式（2-5）等号右边恰恰就是密度函数 的二维傅里叶变换。至此，二维中心切片定理证明完毕。最后，用二维傅里叶变换定理可得到 （2-6） 中心切片定理一般不用于投影重建，因为人们发现，当往 平面一条一条地添加“中心片段”时，中心片段在 平面的原点密度高于远离原点区域的密度（图2.5）。这就意味着高频区域的大片面积是没有中心片段覆盖的，但这些没被覆盖的地方我们不能就这么平白地放着不管，不然就相当于主动丢弃了图像的高频分量，图像质量会大打折扣。怎么办？只好插值了。凡是进行插值，一定会引入大量误差，因此用中心切片定理重建图像时，往往图像的质量不好。 
图2.5：低频区域的片段密度比高频区域高 2.2 直接反投影算法 反投影的定义取决于投影是如何定义的。应当注意一点：反投影绝不是投影的逆运算，反投影算子不是投影算子的逆算子。对图像作原始反投影是无法重建图像的，我们将用一个2×2矩阵说明这一点（图2.5）。 
图2.6：对一个2×2矩阵的投影 红色的数字代表这条投影路径上所有数值的总和。搞图像重建就是将红色的数字重新分配到相应的位置上。怎么分配呢？没别的办法，我们也不知道怎么分，那就均匀地分吧，这条路径上每一个点都分配上这个数值（图2.7）。 
图2.7：按照均匀分配原则重建的矩阵 上述过程被称作“直接反投影算法”。直观上，直接反投影算法是存在很大误差的。其一，单一点位上多个投影值的多次相加使得矩阵每一点总体数值大幅上升。其二，即使每一点数值除以投影线数进行平均化，新数值仍与原矩阵有差距。通过Matlab上的一个小程序演示，我们可以很形象地看到直接投影算法带来的问题（图2.8，图2.9）。 
图2.8：原图像与直接反投影图像对比 
图2.9：原图像与直接反投影之对比 人们将直接反投影算法产生的误差称作“星状尾迹”。星状尾迹产生的根本原因在于：反投影重建的本质是把取自有限物体空间的射线投影均匀地抹回到射线所及的无限空间的各点上，包括原先像素值为零的点。 为了研究直接反投影算法缺陷的解决方案，我们从数学上对直接反投影方法进行一个过程分析。 如果按照信号与系统的思路，将原始密度函数 看作一个输入，将重建密度函数 看作一个输出，那么只要找到了这个系统的冲激响应，就可以设计一个逆系统来恢复原始的 。 假设 ，也就是说系统的输入是位于原点的一个狄拉克 函数，这时的输出就是系统的传输函数。则我们可以推得此输入情况下的投影函数：
（2-8） 如果用极坐标形式表示密度函数 ，将其转换为 ，则
（2-9） 则将 带入式2-9可得
(2-10) 如果密度函数是位于原点的 函数，则投影函数就是位于s=0处的 函数。 那么经过直接反投影重建的密度分布，或者说系统的冲激响应可表示为：
（2-11） 接下来我们还需引入一个关于狄拉克函数的特殊性质才能继续的推导，这个性质可以被描述为（图2.10）： 
图2.10：一个狄拉克函数的性质 将之应用于式2-11
（2-12） 由式2-12可知，从输入 到输出 ，实际上是一个这样的响应过程：
（2-13） 其中， 符号代表二维卷积。 由此观来，直接反投影算法确实会造成图像模糊，而且我们找到了造成模糊的原因。整个反投影系统的冲激响应是 。如果输入一个狄拉克函数，应用直接反投影法，会得到一个带长尾巴的形式的 图像（图2.11）。 
图2.11：长尾巴 形式的图像 我们知道，时域中卷积等于频域中乘积，将变换到频域中得到 （2-14） 所以 （2-15） 根据式2-15可知，在傅里叶变换空间 中把所得到的傅里叶“图像”乘以 ，这个乘积就是 ，对 作二维傅里叶反变换即可得到原函数 。 除此之外，还存在着第二种解决方案，即把投影数据 的一维傅里叶变换 乘上 ，然后，对乘积 作一维傅里叶反变换。这种方法通常被人们称为“滤波反投影（FBP, Filtered Backprojection）”，这种方法相较于前一种先反投影再滤波的算法，应用面要广得多。当然，我们必须证明FBP算法与先反投影再滤波的算法在数学上是严格等价的： 我们首先给出二维傅里叶变换在极坐标形式下的表达式
(2-16) 根据中心切片定理 (2-17)
(2-18) 根据二维傅里叶变换域的对称性，可作如下改写
(2-19) 记 ，同时记 的反变换为
（2-20）
（2-21） 至此，证明完毕。 2.3 滤波反投影算法.方法一 经过上面的推导，我们可以通过在频域对投影函数乘上一个高通滤波器 的方式来抵消直接反投影算法带来的误差。这种先对投影函数进行滤波处理然后进行反投影重建的算法被称作“滤波反投影（FBP, Filtered Backprojection）”。具体过程如下： 求投影函数 的针对变量s的一维傅里叶变换，得到 对 施以高通滤波器 ，得到 对 进行一维傅里叶反变换，得到 ④ 应用 进行反投影，重建图像 此过程可概括为图2.12 
图2.12：典型的滤波反投影过程 同样的，我编写了一个程序，来验证滤波反投影算法。这个程序包括三个部分：第一部分是将图像进行拉东变换，也就是投影；第二部分是对投影函数进行滤波处理；第三部分是进行反拉东变换重建图像。滤波反投影算法取得了不错的效果（图2.13）。 
图2.13：滤波反投影（FBP）算法效果 为深入观察这一过程，我们选取 的投影切片进行观察（图2.14） 
图2.14：θ=0投影值及相应的傅里叶变换 从图2.14中可以清楚地看到，投影函数的低频成分确确实实要比高频成分多得多，相比于低频成分近10^7的数量级，高频成分则低的几乎看不见。顺便一提，通过上图我们也能够看出matlab执行fft操作后实际上输出的是一个严格对称的傅里叶谱（毕竟图像灰度值是实数），以信号长度N为周期，这是其中一个周期的图像，当然matlab也只会提供一个周期的图像。 我们之前的推导全部是基于连续函数的，无论是密度函数还是投影函数都认为是连续的。而在计算机中这些东西无一例外都是离散的。我们应用的FFT（快速傅里叶变换），在计算机中也是离散的，这就是数字信号处理。连续的傅里叶变换与离散形式的傅里叶变换（实际上在本例中应该是DFT，即时域频域全都离散的傅里叶变换）在结果上有一个很大的不同，那便是频率 的意义不同。在离散环境下，傅里叶频谱（Fourier Spectrum）的横坐标，实际上表示的是一个名为“归一化角频率”的东西。这个“归一化角频率” 在matlab中的取值范围是 。也就是说matlab不管原信号实际频率成分如何，在执行了fft操作后它都默认频率范围是 。 所以，如果要乘上个高通滤波器 ，怎么取的值就得仔细考量一下了。我是这样做的（图2.15）： 
图2.15：滤波过程 在频率添加了形如的高通滤波器 后，投影函数的频谱变成了这种形式。我们可以直观地看到各个频率成分都大致相同了，低频成分得到了抑制，高频成分得到了增强（图2.16）。 
图2.16：经过滤波后的投影函数 FPB算法最大的优越性就是省去了一个插值步骤，同时在投影函数上动手脚也比在密度函数上动手脚要省时省力得多。严格来说，插值是不可避免的，反投影过程也涉及到插值，但matlab有着强大的反拉东变换自动插值算法，所以在应用FPB时可以省去插值这一步。 基于上述算法，我们再来做一个实验，看看重建效果与投影角度分辨率之间的关系。所谓角度分辨率，就是 的大小。若我们将 分成20份，那么 就等于9°。根据之前举得公园里的树的例子， 越小，重建效果就越好。我们使用之前滤波反投影的程序，在保证其余部分不变的基础上，仅改变 ，测试下重建效果（图2.17）。 
图2.17：角度数对FPB算法的影响 2.4 滤波反投影算法.方法二 滤波算法不单只有一种实现途径，根据卷积定理，在频域中卷积等于在时域中积分，因此我们不用非得将投影函数 变换到频域再乘上个高通滤波器 了。 这里就涉及到有限长离散变换算法的问题。我们知道，根据信号在频域中的分布，可以通过叠加正弦波的手段在时域中复现这一信号。在本例中，则是知道了 域的分布反求 域的信号。但问题是：正弦波叠加在 域中可是覆盖了 的范围，如果要作卷积运算的话，我们当然希望卷积核能有多短就有多短。应该截取 中的哪一段作为卷积核呢？ 不如这样想一下，我们现在手上已经获得了 ，我们将 看作一个输入序列，将其输入一个系统，这个系统的作用就是高通滤波，最后将得到的输出序列 反投影。滤波系统是一个线性系统，可想而知也是一个时不变系统。对于线性时不变系统，系统的输入输出关系可以完全由其冲激响应 完全描述。首先来看系统是不是因果系统，所谓因果系统，即对于第 个输出样本，其值 仅由 的输入样本 决定。 我认为， 域不同于时域，它是处于空间维度的而不是时间维度的，对于第 个输出样本，其值 仅由 的输入样本 决定是不太现实的，因此这个系统极有可能是非因果的。我们先来看一下高通滤波器 对应 在 域上的分布，MATLAB采用有限长变换IFFT算法，如果原 域序列长度为N，似乎只会列出 的 域序列。既然之前都分析过了系统是非因果的，那么 的时候 便不会满足 这个条件。所以MATLAB返回的 域序列是不可靠的，没办法作为卷积核。在实际实验中亦验证了这一点（图2.18）。 
图2.18：左：原图像；右：重建图像。可以看出MATLAB自带的IFFT算法不能得到正确的卷积核 为了得到能用的卷积核，我编写了一个自创的IFFT算法，这个算法将重建后的s域范围变成了 。重建后的域信号如下（图2.19）： 
图2.19：卷积核 应用该卷积核对 进行卷积，得到的重建图像如下（图2.20）：
图2.20：应用卷积运算重建效果 卷积反投影算法流程描述如下（图2.21） 
图2.21：卷积反投影重建算法 可想而知，卷积核将极大程度上影响最终重建图像的效果。理论上，选取的卷积核长度越长，精度越高，重建效果越好。这个卷积核也被叫做“Ramachandran-Lakshminarayanan”卷积核，假若限制窗函数的截止频率为 ，则根据逆傅里叶变换定理可得：
上面是连续的情况，我们将其离散化，令 ，则有：
绘制出图像如下： 
应用该卷积核重建效果如下： 
2.5 滤波反投影算法.方法三 这里介绍实现高通滤波的第三个方法。我们考虑将高通滤波函数 拆成两部分。
(2-22) 当时，；当时，；当时，. 我们需要用到傅里叶变换的两个性质： 性质1：在傅里叶域（域）中乘以相当于在空间域（域）求微分。 性质2：函数对应的逆傅里叶变换是。与作卷积叫做希尔伯特变换。 希尔伯特变换实际上就是一个90°的移相器，它的作用就是将信号中各个频率成分都移动的相位（图2.22）。 
图2.22：希尔伯特变换对正弦函数的影响 利用式2-22给出的关系，高通滤波器可以这样实现 （2-23） 它是由求导数与希尔伯特变换来完成任务的。 同样的，我编写了一个程序来说明这一点（图2.23） 
图2.23：利用希尔伯特变换重建图像，左为原图像，中为经过一阶求导后的图像，右为进行希尔伯特变换后的图像。 该重建算法的步骤如下（图2.24）： 
图2.24：求导+希尔伯特变化滤波反投影重建算法 我们所做的大部分工作都是在反复更改高通滤波器的实现步骤，有时候在频域实现它，有时候在空间域实现它，有时候现在频域后在空间域，有时候先在空间域后在频域后又在空间域，理论上可以尝试所有的排列组合，根据卷积的交换律可知这并不影响最终结果。 2.6 高通滤波对图像质量的影响 我们对投影函数作了高通滤波，使其能够重建出原始图像。但问题是：噪声信号往往也是高频的。如果一味地增强高频信号，最导致图像的噪声被放大，这显然是不希望看到的。 向图像中加入符合高斯分布的白噪声，可以看到经过高通滤波后，在重建图像中噪点十分密集（图2.25）。 
图2.25：经过高通滤波后噪声被放大 如果想要解决这一问题，必需保证高频成分不要放大地这么高倍。比如使用窗函数来限制高频成分的放大倍数。 
图2.26：余弦滤波与Hann滤波对高频噪声的抑制 2.7 ROI重建法 如果我们只对图像中的一小部分感兴趣，该部分被称作ROI（Region-of-interest, 感兴趣的区域）。在一些情况下，完全可以用不完整的投影数据做出准确的ROI重建，图2.27就举出了这样的情形，因为探测器不够大，不能够把整个物体摄入其内，但可以完整覆盖ROI区域。在断层成像理论中，这个问题叫做内部重建问题。一般而言，内部重建问题只能获得近似解，而在某些情况下可以得到精确解。 
图2.27：在某些情况下不完整的数据亦可重建完整ROI 探测器的视野是个圆形区域，而ROI是其中更小的黄色部分。我们使用DBH运算重建图像。求导运算和反投影运算都是局部运算，也就是说，运算结果只与近邻的数据有关。对于被截断的数据，在求导与反投影后，所得的中间结果在视野内仍可认为是一致准确的。 重建算法的下一步是沿着探测器方向作希尔伯特变换。根据之前的结论，希尔伯特变换实际上就是一个卷积积分，它的卷积核为。所以我们需要知道整条积分线上的数值。对于不完整的投影数据，这个要求无法达成。 好在存在一个有限的希尔伯特变换，我们可以用有限区间内的数据来求精确的希尔伯特反变换。设函数只在区间上非零，的希尔伯特变换为，那么有限的希尔伯特反变换公式只需用到在区间上的值来恢复出原本的来。 另一种解析开拓的方法可能更好用一些，假如在视野内有一个小小的已知区域，原本的图像在这个小区域内是已知的。我们可以使用迭代的方式重建。解析开拓是复变函数中的一个分支，复变函数是数学中的一个分支，它研究的函数是以复数为变量的。（图2.28） 
图2.28：利用迭代解析开拓重建ROI 三、迭代重建 3.1 解线性方程组 开头提到过一种不用反投影而是通过解线性方程组的方法来求得密度函数中每一个点的数值。解方程的方法并不是万能的，即使选取足够多的角度去作投影，往往最后得到的方程组是不相容的，因为常常会混进去许多噪声干扰，影响重建质量。 比如我们可以假设处这样一种情况：用一个3×3的矩阵表示密度函数，存在三个投影方向，存在三个探测器，则我们可以列出9个方程（图3.1，图3.2）。 
图3.1：用3×3的矩阵表示密度函数 
图3.2：3×3矩阵对应的方程组 这个方程组也可以用矩阵的方式给出： (3-1) 如果矩阵A可逆的话，也就是存在一个逆矩阵，重建的图像就可以这样得到： （3-2） 在通常的医学成像应用中，方程的系数矩阵A十分庞大，无法同时储存在计算机内部。处理时只能提取某一行或者某一列来读取，处理结果也不能完整保存，而是以中间值到最终结果的形式进行保存。当我们对该矩阵进行转置或者其他操作时就会显得非常麻烦。因此解系数方程的方法并不适用于通常意义上的医学图像重建。 3.2 代数重建算法（ART） ART（Algebraic Reconstruction Technique）算法有时候也被称作Kaczmarz算法，它的思路是：让当前的图像在一次更新中满足系数方程组其中的一个方程。如（图3.3）图中的三条直线代表着三个方程组，存在两个未知数，可以构建出一个二维空间。 
图3.3：系数矩阵空间 其中，是设定的一个初始值。将朝L1上投影，就得到了，以此类推，可以证明最终会收敛到多条直线的交点，也就是该系数矩阵的最终解。 如果这个方程组是不相容的，这个算法会导致方程组的“解“来回跳动而不会收敛，我们需要设定一个迭代阈值来限制该种情况的发生（图3.4）。 
图3.4：不相容的方程组 3.3 梯度下降算法 为了评价迭代算法的性能，首先构造一个评价函数： （3-3） 显然，这个目标函数值越小，最终的重建效果就越好，由于噪声的影响，这个方程组是不相容的，目标函数的极小值是一个非零的正值。 梯度下降算法的策略是：对于当前的图像求其目标函数的梯度，根据梯度把估算的图像往目标函数极小值方向推。在一维情况，梯度就是函数的导数，梯度方向是函数上升方向，与梯度方向相反的方向是函数下降的方向。梯度下降算法则是选取与梯度相反的方向对函数进行更新，每一次更新步长要取得很小，以保证算法可以收敛到极小值。 如果图像是欠定的，那么这个最小二乘问题解不唯一，目标函数存在一个长长的峡谷。在这种情况下，算法收敛所得到的解取决于给定的初始条件（初始图象）。如果初始图像是零，即，那么这个算法将得到最小范数解。 由于噪声的影响，方程组是不相容的，当迭代数很大时，所得的图像可能会被噪声淹没。当迭代数很小时，图像主要含有低频分量；当迭代书逐渐增大时，高频分量逐渐侵入，噪声也逐渐加入。 对于实际问题，梯度方向是很容易利用投影和反投影计算的，其计算式为。但是，负的梯度方向未必就是寻找极小值的最佳方向。一个最佳的例子来自于梯度等高线图，这些等高线是一些椭圆。在任一点的梯度方向与在那一点的椭圆的切线方向是垂直的。这样梯度下降过程弯曲而又曲折，既费时又费力（图3.5）。 
图3.5：负的梯度方向不一定是寻找函数极小值的最佳方向 而改用共轭梯度方向来搜索要比用梯度方向搜索有效得多。所谓和是这样定义的：. 目标函数的形状特征是包含在方阵中的。当我们运用共轭方向的时候，我们实际上是先把等高线进行变换，把它们变成同心圆，然后再找正交方向。利用共轭梯度方向可以使算法收敛的更快一些（图3.6）。 
图3.6：使用共轭梯度法比梯度方向更为有效一点 3.4 ML-EM（最大期望值最大似然函数）算法 除了使用最小二乘法创建评价函数外，还可以通过其他途径来创建它。如果我们使用泊松噪声模型或仅仅使用非负值约束，我们就可以得到一个特别的目标函数，对这个目标函数求极小值，可得到一个用乘法来更新图像的算法，叫ML-EM算法。这个算法可以写作： （3-4） 其中是个素全为1的向量，其素个数与投影数据向量素个数相同。这个算法的特点是使用除法而不是加减法来更新图像。它还有一个很重要的特性：如果给定的初始图像没有负值的话，迭代后的结果永远不会出现负值。 这个算法的目标函数可以设置成一个似然函数，它就是泊松随机变量的联合概率密度函数。我们希望找到一个解来使这个似然函数取得极大值，因此，这个算法叫ML（Maximum Likelihood最大似然）算法。 通常，在求一个函数的极大值或极小值时，我们总是对其所有的变量求偏导，令这些偏导数等于零，并解出这些未知数。对于泊松似然函数而言，利用偏导求解其未知数有些困难。为了简化方程式，我们把方程式中的一些随机变量用其期望值来代替，接下来就是求其最大值，这就是最大期望值的来历（Expectation Maximization）。 这个ML-EM算法亦被称作Richardson-Lucy算法，因为Richardson和Lucy分别在1972年和1974年作图像去模糊研究时提出了这个算法。在不同行业有不同的EM算法。 四、总结 上述图像重建算法是比较基础的算法，可以说各有利弊。例如滤波反投影重建算法，让投影函数通过高通滤波器必然会导致高频噪声部分受到放大，影响了图像质量；又比如根据中心切片定理重建图像，需要解决插值问题。 总的来说，这些方法的实际意义都非常强，比如介绍过的截断数据ROI成像技术，本文提到了可用解析开拓的手段复现截断数据，这意味着图像中必须存在一块区域，我们提前已知这块区域的密度信息，这不禁让人联想能否在人体中植入某种规则形状的材料，来帮助我们重建ROI区域图像。 除了平时束投影外，临床上常用扇形束扫描技术、三维螺旋扫描技术进行造影。除了CT外，还有MRI、PET、SPECT等技术用于医学成像。MRI、PET、SPECT等技术与CT成像的意义不同，CT反映的是人体组织对X射线的吸收程度，而PET、SPECT则是统计某一位置处辐射出的γ光子的数量。因此相同的算法在处理不同的问题时还需要更新与修正。 五、参考文献 [1] 曾更生.《医学图像重建入门》.高等教育出版社.2009 [2] 高上凯.《医学成像系统》.清华大学出版社.2010
2024最新激活全家桶教程，稳定运行到2099年，请移步至置顶文章：https://sigusoft.com/99576.html
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请联系我们举报，一经查实，本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处：https://sigusoft.com/64734.html
