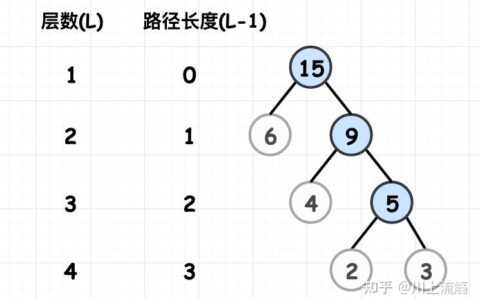
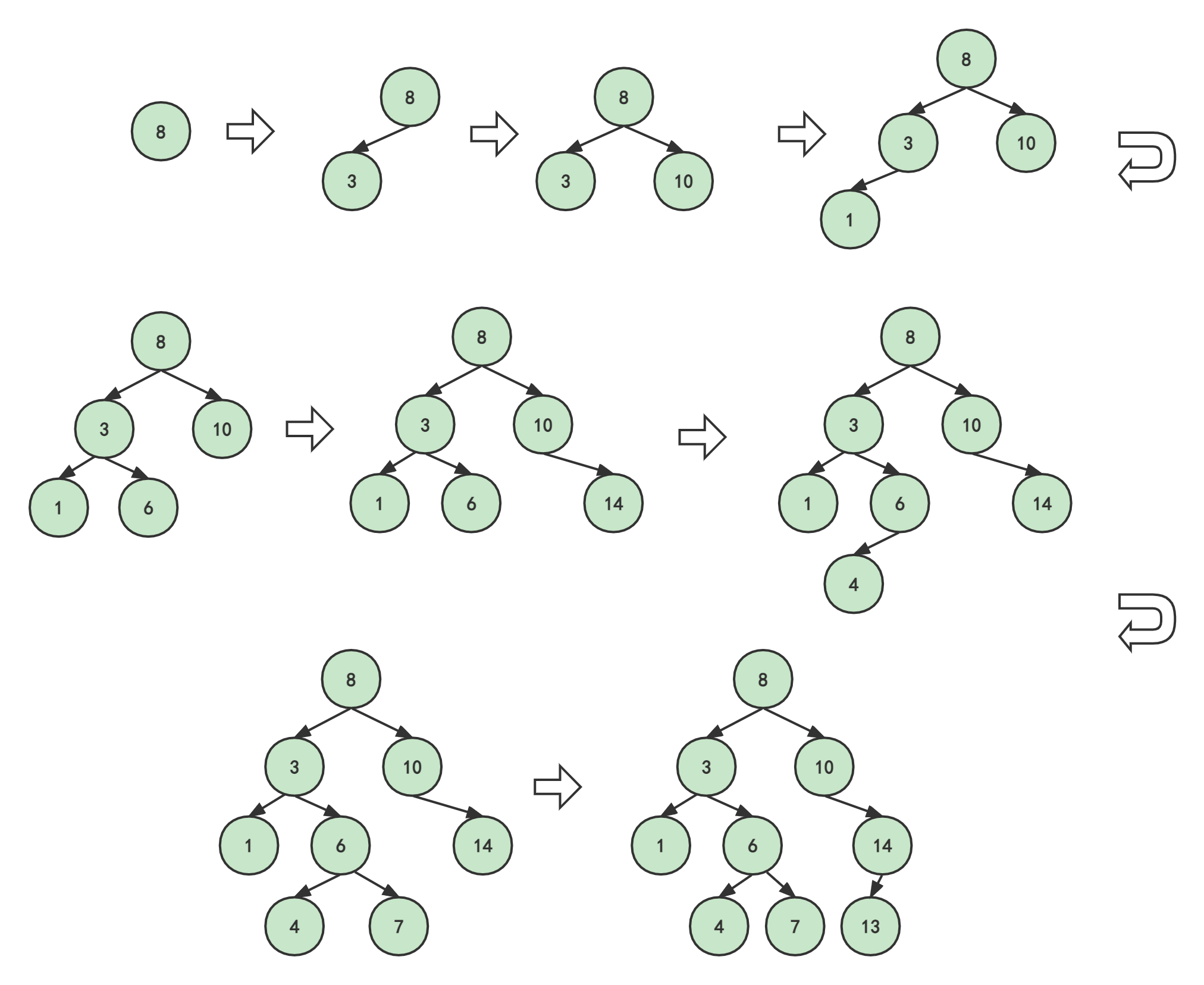
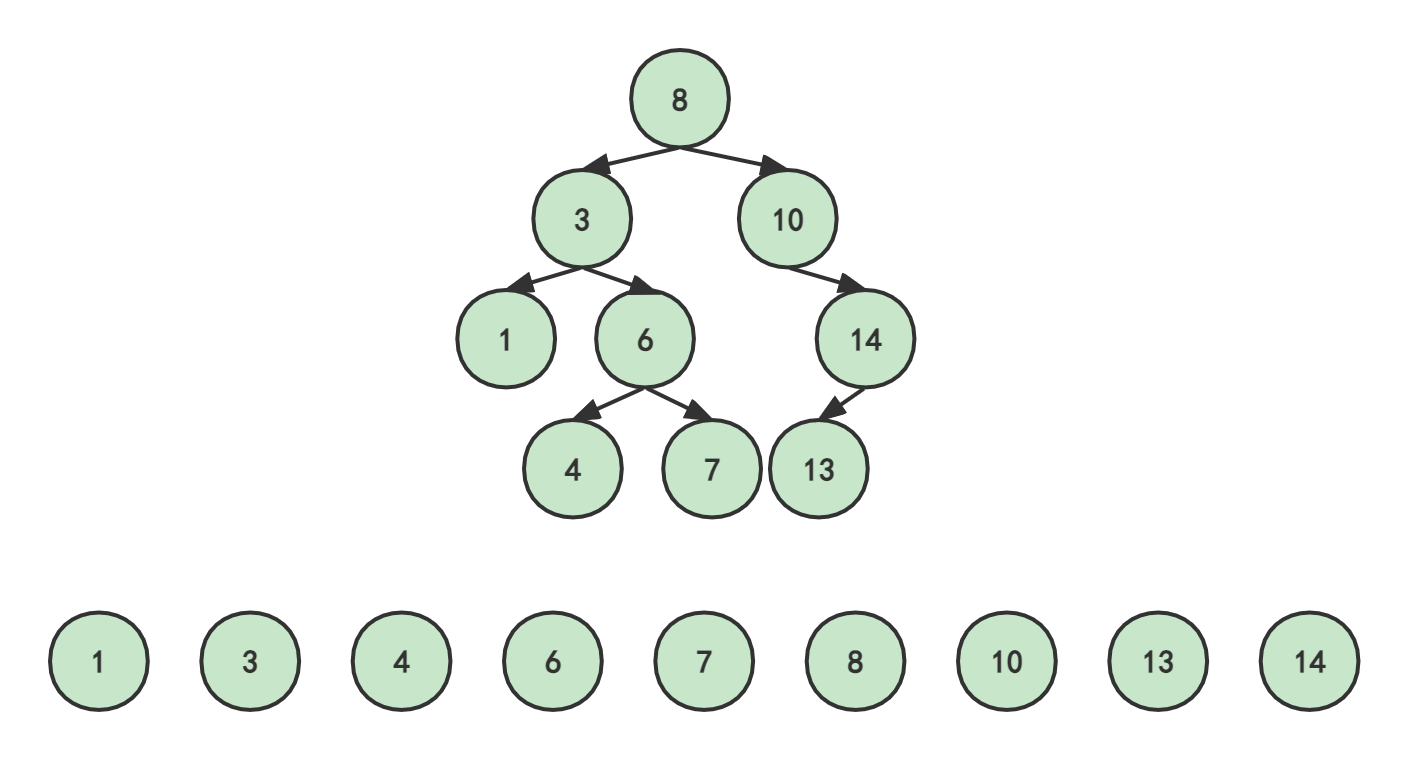
二叉排序树（二叉查找树、二叉搜索树）（图解+完整代码） 目录 ⚽1.什么是二叉排序树 🏐2.构建二叉排序树 🏀3.二叉排序树的查找操作 🥎4.二叉排序树的删除 🎱5.完整代码 ⚽1.什么是二叉排序树 我们直接看它的性质： 若它的左子树不空，则左子树上所有结点的值均小于它根结点的值。若它的右子树不空，则右子树上所有结点的值均大于它根结点的值。它的左、右树又分为⼆叉排序树 显然，二叉排序树与二叉树一样，也是通过递归的形式定义的。因此，它的操作也都是基于递归的方式。 二叉排序树也叫二叉查找树、二叉搜索树，既然名字都不一般，那它显然和普通的二叉树不同。那到底有什么不同，它的特点或者优点在哪里呢？不妨，我们来构建一棵二叉树。 🏐2.构建二叉排序树 假设我们有以下数据，我们按从左到右的顺序来构建二叉排序树： 
首先，将8作为根节点插入3，由于3小于8，作为8的左子树插入10，由于10大于8，作为8的右子树插入1，由于1小于8，进入左子树3，1又小于3，则1为3的左子树插入6，由于6小于8，进入左子树3，6又大于3，则6为3的右子树插入14，由于14大于8，进入右子树10，14又大于10，则14为10的右子树插入4，由于4小于8，进入左子树3，4又大于3，进入右子树6，4还小于6，则4为6的左子树插入7，由于7小于8，进入左子树3，7又大于3，进入右子树6，7还大于于6，则7为6的右子树插入13，由于13大于8，进入右子树10，又13大于10，进入右子树14,13小于14，则13为14的左子树 经过以上的逻辑，这棵二叉排序树构建完成。 
我们可以看出： 只要左子树为空，就把小于父节点的数插入作为左子树只要右子树为空，就把大于父节点的数插入作为右子树如果不为空，就一直往下去搜索，直到找到合适的插入位置 了解了如何构建后，我们不禁要问，这有啥用呀？感觉没啥特别的地方呢？别急！我们马上揭晓！ 我们对这棵二叉树进行中序遍历，看看会发生什么？你自己试一试！ 没错，这棵二叉树中序遍历结果为： 
根据以上思路，我们其实就可以写出代码了，构建的过程其实就是插入的过程： 🏀3.二叉排序树的查找操作 它既然也叫二叉查找树，那想必会非常方便我们查找吧！它的操作并不是把中序遍历的结果存入数组，然后在有序数组里查找，而是直接在树上查找。其操作与二分查找非常相似，我们来查找7试一试？（这里要说明以下：在正常的数据结构中，由于数据量很大，所以我们也不知道我们想要的素在不在里面；同时也不知道每个素具体是多少，只知道他们的大小关系。我们是在此基础上进行查找） 首先，访问根节点8根据性质，7比8小，所以如果7存在，那应该在8的左子树那边，访问8的左子树访问到了3，根据第2步的思想，访问3的右子树访问到了6，继续访问6的右子树访问到了7，刚好找到啦！ 
显然，它的效率会比在无序数组中挨着查找快多了吧！我们直接上代码。 🥎4.二叉排序树的删除 那么删除就稍微比查找与插入复杂一点，因为需要分类讨论了。 1.被删除结点为叶子结点 直接从二叉排序中删除即可，不会影响到其他结点。例如删去7： 
2.被删除结点D仅有一个孩子 如果只有左孩子，没有右孩子，那么只需要把要删除结点的左孩子连接到要删除结点的父亲结点，然后删除D结点；如果只有右孩子，没有左孩子，那么只要将要删除结点D的右孩子连接到要删除结点D的父亲结点，然后删除D结点。 以D=14为例：它没有右孩子，只有左孩子。（先把10指向14的右指针移动，去指向13，然后再删除14） 
再以D=10为例，它没有左孩子，只有右孩子。（先把8指向10的右指针移动，去指向14，然后再删除10） 
3.被删除结点左右孩子都在 这种情况就要复杂很多了。但没有关系，依然会讲的很清楚。 我们先假设删除根节点8，看看会发生什么？ 
我们的目标依然是要保证删除结点8后，再次中序遍历它，仍不改变其升序的排列方式。 那么我们只有用7或者10来替换8原来的位置。 我们先看7来顶替位置 
此时7从叶子结点“升迁”到了根节点（只是刚好要删除的结点为根节点，如果删除3，就替换3的位置） 我们再看10来顶替位置 
这时候我们就应该会产生两个问题： 为什么是7或者10来替换8的位置？ 显然，7与10是挨着8的，如果用其他素替换则会打扰其顺序。 那7和10怎么在二叉排序树中找到呢？ 显然，7在8左子树的“最右边”，10在8右子树的“最左边”。根据二叉排序树的插入方式，比8小的素一定在左子树，而我们又要找到比8小的最大的数，这样才能保证他们俩在顺序上是挨着的，所以它又会在8的左子树的最右边。同理也可以找到10. 根据此方法，我们可以直接给出代码 🎱5.完整代码 本结就到这里啦，感谢你的支持！
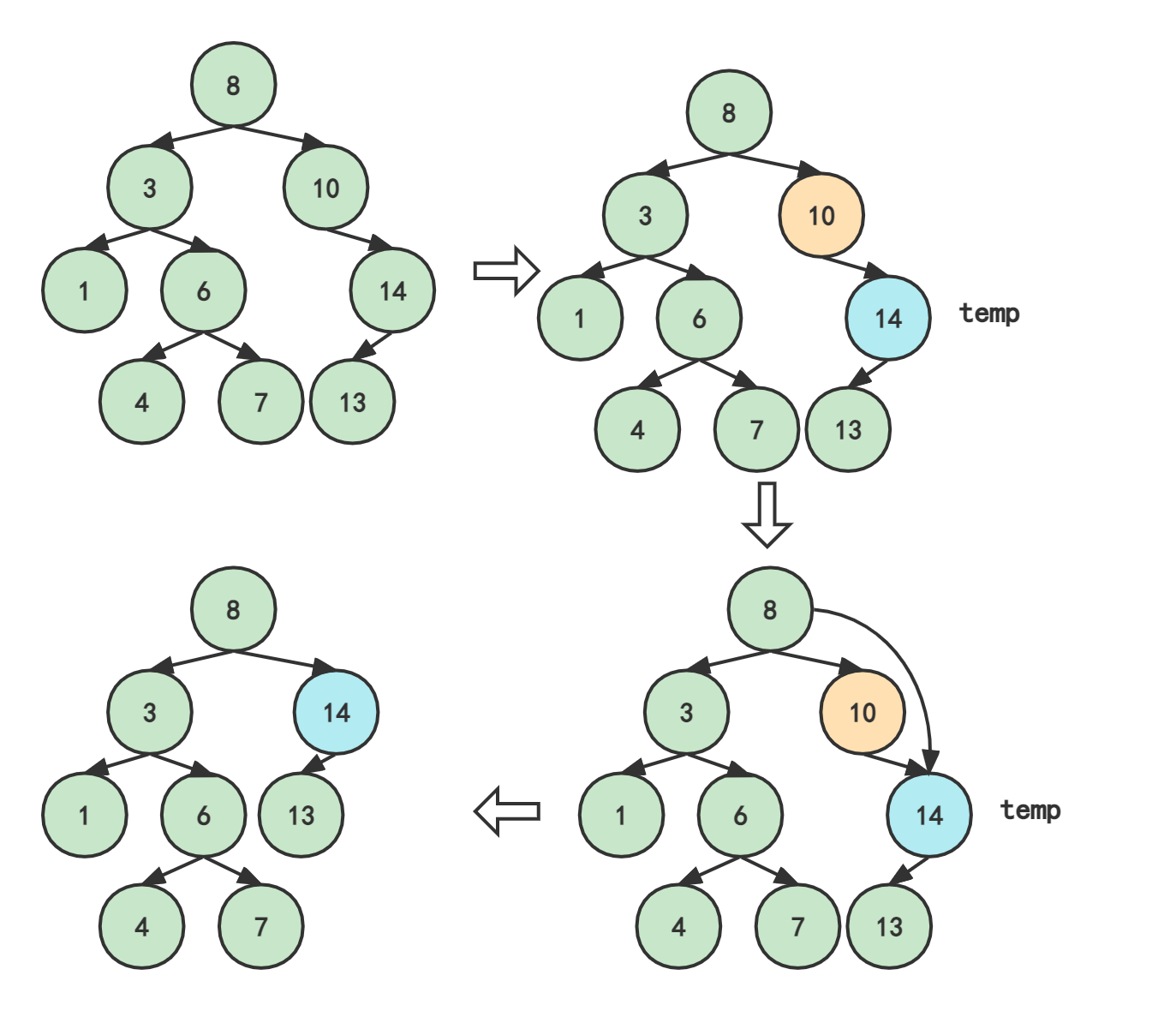
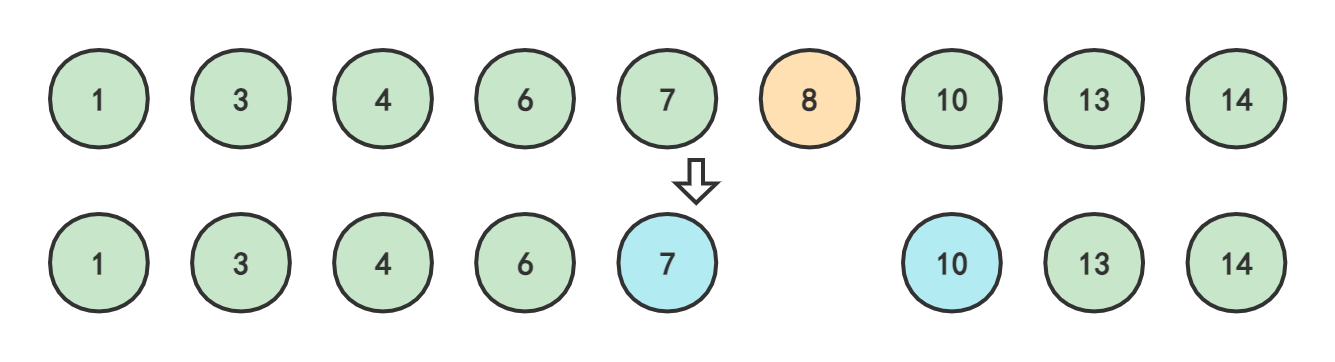
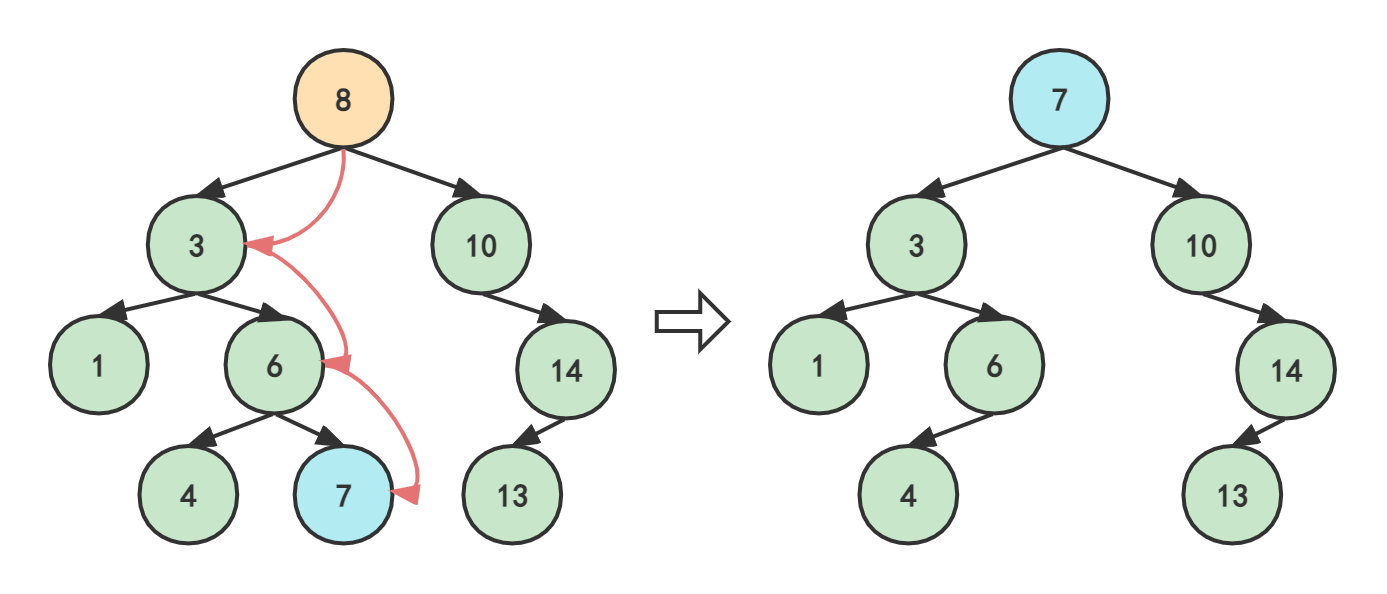
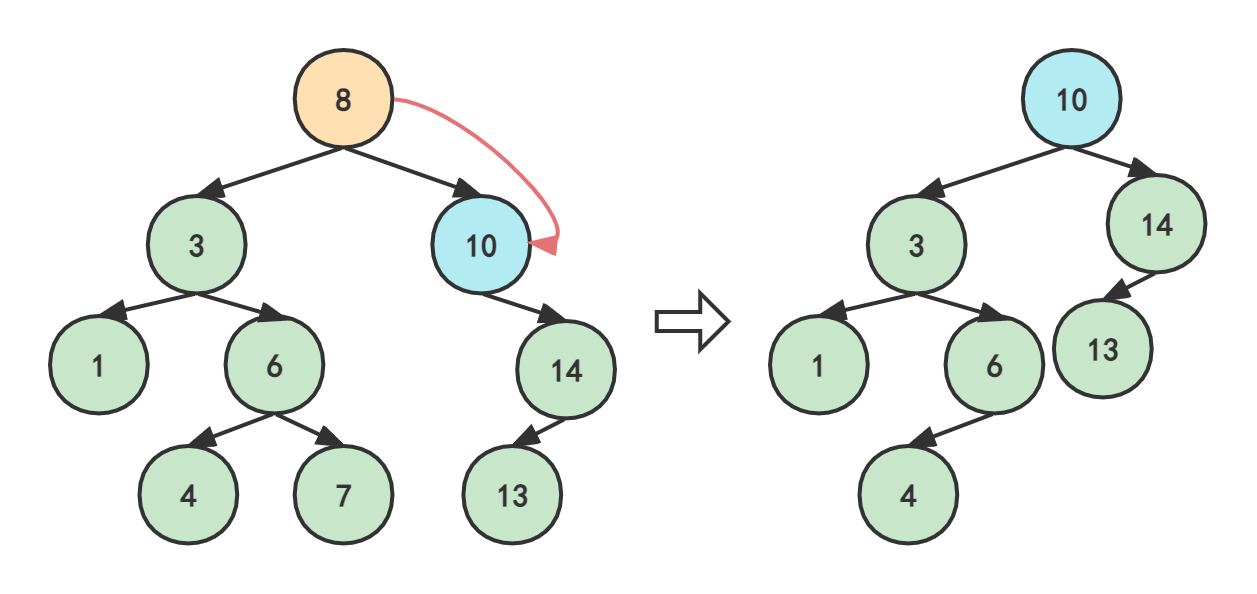
2024最新激活全家桶教程，稳定运行到2099年，请移步至置顶文章：https://sigusoft.com/99576.html
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请联系我们举报，一经查实，本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处：https://sigusoft.com/46664.html
