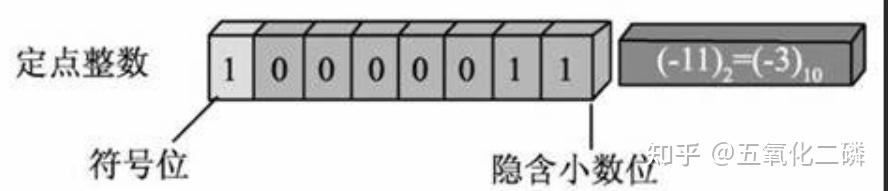
计算机组成原理总结-2.1.数值表示 写在前面: 之前零零碎碎的总结过一些计算机组成原理的概念,但总是感觉不够精细与准确,之后我会定期更新一些与计组相关的内容,希望对大家有所帮助~ #1.数制与编码 ## 1.1.进制计数制及其相互转换 想必大家都了解计算机是通过二进制来进行存储的,但是为什么需要二进制编码呢?主要有以下几个原因:二进制中只有两种状态,使用具有两个状态的物理器件便可以表示二进制数中的每一位,成本较低。例如通过高低电平和电荷正负可以很方便的表示0和1.二进制中的0和1刚好可以对应逻辑运算中的“真”与“假”,使用二进制可以很方便的进行逻辑运算。二进制的编码和运算都十分简单,可以通过逻辑电路来实现算术运算。 进制表示 常用的进制有十进制、二进制、八进制和十六进制。十进制是日常生活中使用最多的。而计算机中通常使用二进制数。八进制和十六进制有利于和二进制的转换。 十进制:0-9,逢十进一 二进制:0-1,逢二进一 其余类似。 例如:1001,在十进制中,表示一千零一;在二进制中,表示8+1=9;而在十六进制中,表示16^3+1 进制转换 对于一个二进制混合数(含有整数和小数),在转换时以小数点为中心,向左右两端扩散。 八进制是3位一组,十六进制是4位一组。 例如: .011010 八进制: 001 111 000 010 . 011 010 ——(1702.32)8 十六进制:0011 1100 0010 . 0110 1000 ——(3C2.68)16 如果需要将任意进制数转换为十进制,则需要各位的数码与它们对应的权值相乘,最终相加。例如: (162.4)7 = 1*(7^2) + 6*(7^1) + 2*(7^0) + 4*(7^-1) 如果需要将十进制数转换为任意进制数,则通常采用基数乘除法。对整数部分和小数部分分别处理: 例如:123.6875转换为二进制数 123/2=61 — 123%2=1 61/2=30 — 61%2=1 30/2=15 — 30%2=0 15/2=7 — 15%2=1 7/2=3 — 7%2=1 3/2=1 — 3%2=1 1/2=0 — 1%2=1 最终整数部分表示为: 而对于小数部分: 0.6875*2 = 1 + 0.375 0.375 * 2 = 0 + 0.75 0.75 * 2 =1 + 0.5 0.5*2 = 1 最终小数部分表示为:1011 则二进制表示为:(.1011)2 需要注意的是,并不是每一个十进制小数都可以被转换为其他进制,通常需要取精度。 真值和机器数 在日常生活中,通常用正负号分别表示正数和负数,这种带有具体+-号的数被称为真值。真值是机器数所代表的实际值。 在计算机中,通常将数字的符号和数值一起编码,将符号数字化。通常0表示正,1表示负,把这种符号化的数字称为机器数。通常有原码、反码和补码表示法。 ## 1.2.定点数的编码表示 根据小数点的位置是否固定,在计算机中有两种数据格式:定点表示与浮点表示。在现代计算机中,通常用定点补码整数表示整数,用定点原码小数表示浮点数的尾数部分,用移码表示浮点数的阶码。 上边我们都提到:原码、反码、补码、移码、阶码这些好多码的概念,为了防止混淆,下面我将一一具体介绍。但是在介绍之前,我们还需要先了解一下定点表示的基本概念: 机器数的定点表示: 定点表示可以表示定点小数和定点整数。 定点小数:纯小数,小数点在符号位之后、有效数值最高位之前。若数据X的形式为X=x0x1…xn,其中x0表示符号位,x1-xn是数值的有效部分,也称为尾数,x1是最高有效位,则在计算机中表示如下: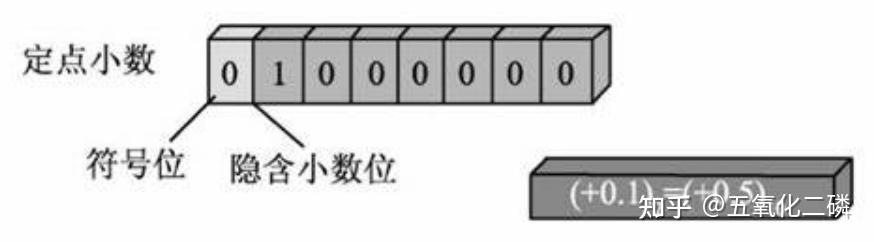
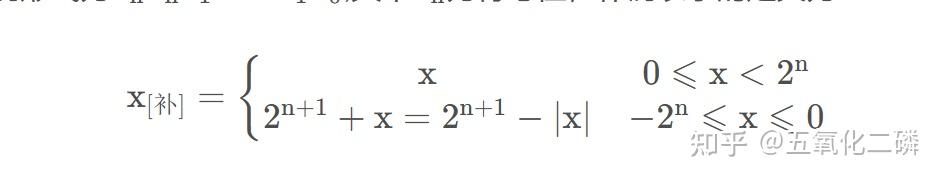
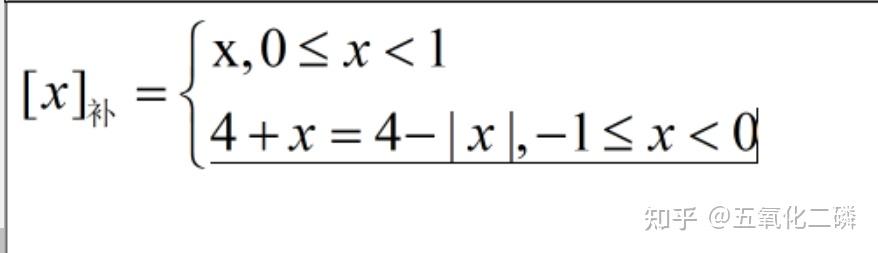
2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/41146.html