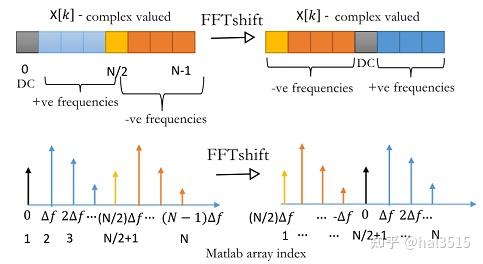
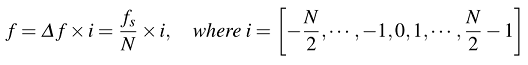数字信号处理1:完全掌握Matlab中的FFT 大三下半学期的时候我学习了数字信号处理这门课程,理论部分的新内容实际上并不多,基本都是继承自信号与系统这门课,但是令人迷惑的地方也还真是不少,尤其是从连续变换到离散,很多特性都有了很大的变化,我基本上学完之后还是处于比较迷糊的状态,所以就慢慢通过仿真梳理一下里面的难点,争取让自己理解的更深入。 今天先来谈一谈傅里叶变换,主要从仿真切入。这篇博客的前置知识是DFT(IDFT)、FFT(IFFT)的一些最基本的概念,主要取材于 Wireless Communication Systems in MATLAB 这本书。 一、基本公式 离散傅里叶变换中有两个最基本的公式,一个是 DFT ,另一个是 IDFT。考虑长度为 N 的时域复信号 x[n],它通过 N 点的 DFT 就可以变成长度为 N 的频域复信号 X[k],反过来从频域变换到时域就是 IDFT 了。 具体的公式如下: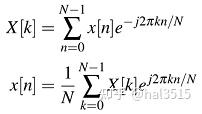
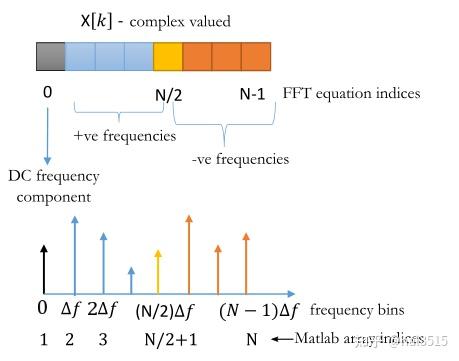
![用fft对信号进行频谱分析总结_matlab绘制频谱插图9 \small X[0]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)









2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/39887.html