构造哈夫曼树的四句口诀_哈夫曼树只有度为0和度为2[数据结构]哈夫曼树&K叉哈夫曼树&范式哈夫曼编码&编码位数的限制方法最近在编写JPEG编解码器,学习了有关哈夫曼树,哈夫曼编码的知识,故用此篇文章记录。哈夫曼树是一种特别经典的树,又称最优二叉树。哈夫曼树是带权路径长度达到最小的树,权值大的离根近,其最经典
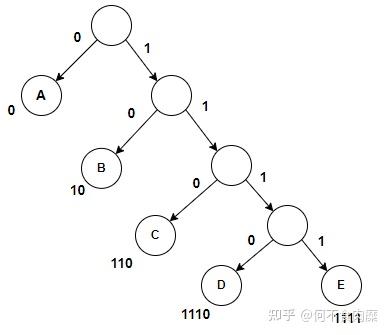
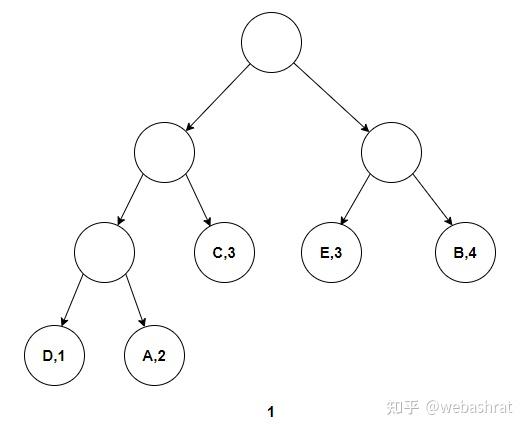
[数据结构]哈夫曼树&K叉哈夫曼树&范式哈夫曼编码&编码位数的限制方法 最近在编写JPEG编解码器,学习了有关哈夫曼树,哈夫曼编码的知识,故用此篇文章记录。 哈夫曼树是一种特别经典的树,又称最优二叉树。哈夫曼树是带权路径长度达到最小的树,权值大的离根近,其最经典的应用就是哈夫曼编码。 哈夫曼树和哈夫曼编码 编码就是将某些符号或者信息从一种形式或格式转换为另一种形式的过程。例如AABCDE这6个字母,直接存ASCII值会占用48比特,如果用000表示A,001表示B,010表示C,011表示D,100表示E这6种二进制表示它,这6个字母的编码便是00000000 总共占用18比特,起到了压缩和加密的效果。 但这种编码不是最优的,实际上,如果用0表示A, 10表示B,110表示C,1110表示D,1111表示E,上面的编码就变成0011,共15比特,比18比特少了3比特,而且编码是不会产生歧义的。 哈夫曼树一种寻找符号对应的编码,使得其编码后的长度最短的工具。通过构造哈夫曼树,便可以得知对应符号的编码为多少时,总编码长度最小。得到的编码便是哈夫曼编码。实际上,上面的15比特的编码方法就采用如下的哈夫曼树得来。从根节点沿着树的路径走,左节点表示0,右节点表示1,叶子表示相关符号,这样便可得知其编码。

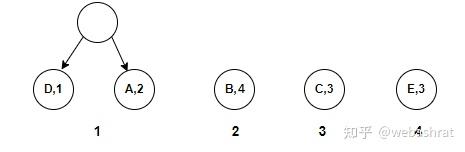
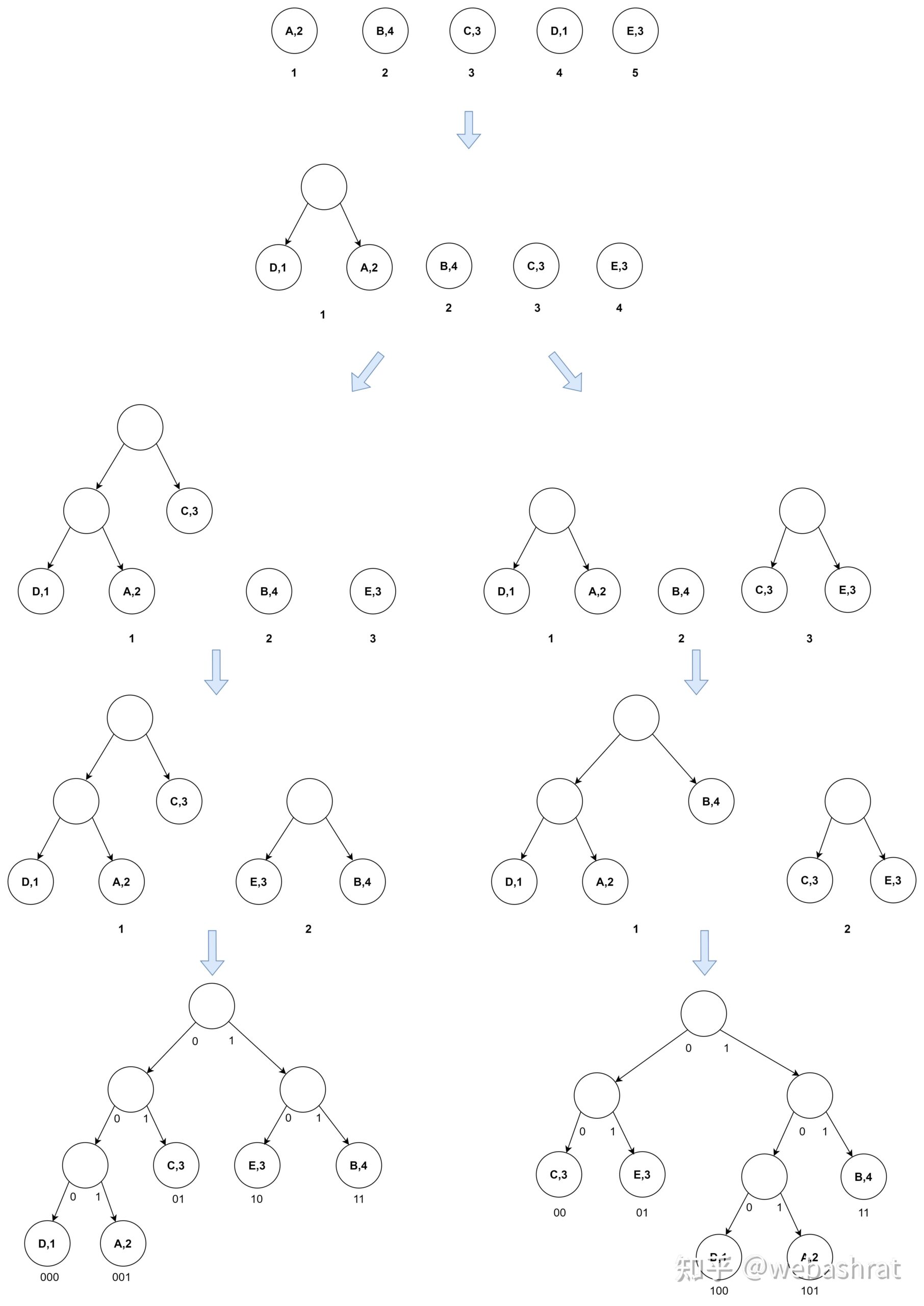
 从哈夫曼树可以看出,得到的符号是不会有歧义的。计算机从左往右读取数据,如果编码有歧义,说明某个编码是另一个编码的前缀,例如0和01就有歧义,当读取到0时,不知道是0对应一个符号,还是与后面的1结合,01对应一个符号。上面的歧义在树上的表现就是某个符号对应的节点是非叶子节点,而哈夫曼编码规定待编码的符号是与叶子节点绑定的,因此不会产生歧义。 哈夫曼树是带权路径长度达到最小的树,这句话的意思是每个节点的权值*路径长度的总和最小。上面的哈夫曼树,如果用AABCDE各个字母出现的频数为上面的哈夫曼树叶子节点权值,其他节点权值为0,那么上面的节点的权值路径长度的总和为 2*1+1*2+1*3+1*4+1*4=15,这刚好是AABCDE采用哈夫曼编码后的长度。而且可以发现,出现两次的符号A被赋予了最短的编码。实际上,哈夫曼编码正是利用了哈夫曼树这一性质,一般情况下,如果一段数据是由有限个符号构成的,计算那些符号出现的频数并作为哈夫曼树的叶子节点的权重,所得的编码便是最短的。 哈夫曼树的构造方法 构造哈夫曼树的方法非常简单。假设要编码这么一段字符串:”ABEBBBAEECCDC”,这个字符串共ABCDE 5个符号,由2个A, 4个B,3个C,1个D,3个E构成,那么 ①设有5个孤立的节点,每个节点权重分别为2,4,3,1,3这5个孤立的节点可以看作是由5棵只由一个根节点构成的树所构成的森林,每棵树的重量(树的所有节点权值之和)分别为2,4,3,1,3。
从哈夫曼树可以看出,得到的符号是不会有歧义的。计算机从左往右读取数据,如果编码有歧义,说明某个编码是另一个编码的前缀,例如0和01就有歧义,当读取到0时,不知道是0对应一个符号,还是与后面的1结合,01对应一个符号。上面的歧义在树上的表现就是某个符号对应的节点是非叶子节点,而哈夫曼编码规定待编码的符号是与叶子节点绑定的,因此不会产生歧义。 哈夫曼树是带权路径长度达到最小的树,这句话的意思是每个节点的权值*路径长度的总和最小。上面的哈夫曼树,如果用AABCDE各个字母出现的频数为上面的哈夫曼树叶子节点权值,其他节点权值为0,那么上面的节点的权值路径长度的总和为 2*1+1*2+1*3+1*4+1*4=15,这刚好是AABCDE采用哈夫曼编码后的长度。而且可以发现,出现两次的符号A被赋予了最短的编码。实际上,哈夫曼编码正是利用了哈夫曼树这一性质,一般情况下,如果一段数据是由有限个符号构成的,计算那些符号出现的频数并作为哈夫曼树的叶子节点的权重,所得的编码便是最短的。 哈夫曼树的构造方法 构造哈夫曼树的方法非常简单。假设要编码这么一段字符串:”ABEBBBAEECCDC”,这个字符串共ABCDE 5个符号,由2个A, 4个B,3个C,1个D,3个E构成,那么 ①设有5个孤立的节点,每个节点权重分别为2,4,3,1,3这5个孤立的节点可以看作是由5棵只由一个根节点构成的树所构成的森林,每棵树的重量(树的所有节点权值之和)分别为2,4,3,1,3。

 ②从“森林”中选出重量最小的2棵树,组成一个新树,需要一个新节点作为父节点连结它们,新添加的父节点权值总是为0,且重量小的作为新添加的父节点的左儿子,重量较大的作为新添加的父节点的右儿子。 根据过程②的规则,选择4,1两棵树组成新树,视图变成:
②从“森林”中选出重量最小的2棵树,组成一个新树,需要一个新节点作为父节点连结它们,新添加的父节点权值总是为0,且重量小的作为新添加的父节点的左儿子,重量较大的作为新添加的父节点的右儿子。 根据过程②的规则,选择4,1两棵树组成新树,视图变成:

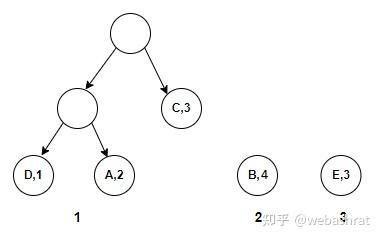
 重复过程②,可以选择1,3两棵树组成新树。视图变成:
重复过程②,可以选择1,3两棵树组成新树。视图变成:

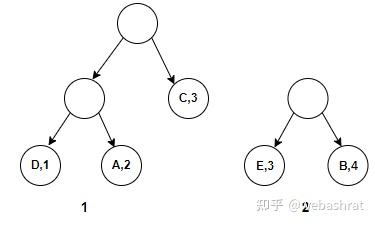
 继续重复过程②,选择2,3两棵树组成新树。视图变成:
继续重复过程②,选择2,3两棵树组成新树。视图变成:

 继续重复过程②,选择1,2两棵树组成新树,注意重量大的树在右,轻的在左。视图变成:
继续重复过程②,选择1,2两棵树组成新树,注意重量大的树在右,轻的在左。视图变成:

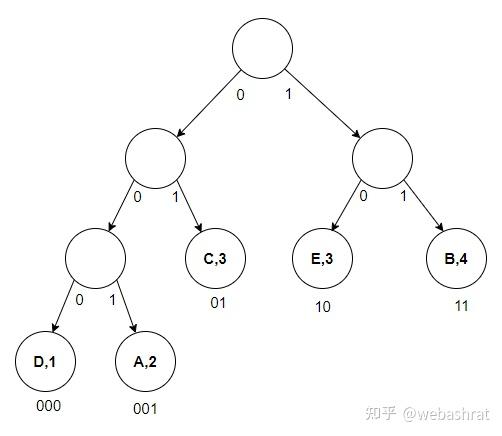
 这便是我们得到的哈夫曼树。从根节点沿着树的路径走,左节点表示0,右节点表示1,叶子表示相关符号,这样便可得知ABCDE这5个符号的哈夫曼编码。
这便是我们得到的哈夫曼树。从根节点沿着树的路径走,左节点表示0,右节点表示1,叶子表示相关符号,这样便可得知ABCDE这5个符号的哈夫曼编码。

 根据哈夫曼树可知,频数高的符号被赋予了位数更多的二进制数码,相应的节点深度也更深。 同时得到了ABCDE这5个符号对应的哈夫曼编码为符号频数编码A2001B411C301D1000E310 总结上面的哈夫曼树的生成过程,可以得知如下构造哈夫曼树,获得哈夫曼编码的步骤: ①确定一段数据由N个不同的符号组成,计算N个不同的符号出现的频数 ②初始化N个孤立树节点,也就是N个只有1个根节点的树,构成一个森林。N个节点与N个符号对应,节点的权值为对应的符号出现的频数。 ③从森林中每次选取2个重量最小的树。定义一个新节点作为父节点连接这2棵树,较轻的树作为左儿子,较重的作为右儿子(也可以反过来)。(森林中树的个数每次减一) ④重复过程③,直到只剩下一棵树 ⑤最后一棵树便为哈夫曼树。从根节点沿着树的路径走,左节点表示0,右节点表示1(当然也可以反过来),即可得知对应符号的哈夫曼编码。 哈夫曼树的构造代码非常简洁。其中,过程③将涉及在一个容器中,每次容器中作为最值的素,还要保证添加或删除素要保证能正确返回容器中作为最值的素。这正是堆结构的典型应用场景。因此哈夫曼树的构造过程应当在堆容器中进行,C++中可以使用std::priority_queue. 哈夫曼树的同权不同构 上面针对字符串”ABEBAEECCDC”生成对应的哈夫曼树的过程中,在生成树的第3步中,是将1,3两棵树合并,但是实际上,还可以将3,4两棵树合并,因为出现了多棵树的重量相同的情况。这种情况下不同的合并策略会生成不同的哈夫曼树。
根据哈夫曼树可知,频数高的符号被赋予了位数更多的二进制数码,相应的节点深度也更深。 同时得到了ABCDE这5个符号对应的哈夫曼编码为符号频数编码A2001B411C301D1000E310 总结上面的哈夫曼树的生成过程,可以得知如下构造哈夫曼树,获得哈夫曼编码的步骤: ①确定一段数据由N个不同的符号组成,计算N个不同的符号出现的频数 ②初始化N个孤立树节点,也就是N个只有1个根节点的树,构成一个森林。N个节点与N个符号对应,节点的权值为对应的符号出现的频数。 ③从森林中每次选取2个重量最小的树。定义一个新节点作为父节点连接这2棵树,较轻的树作为左儿子,较重的作为右儿子(也可以反过来)。(森林中树的个数每次减一) ④重复过程③,直到只剩下一棵树 ⑤最后一棵树便为哈夫曼树。从根节点沿着树的路径走,左节点表示0,右节点表示1(当然也可以反过来),即可得知对应符号的哈夫曼编码。 哈夫曼树的构造代码非常简洁。其中,过程③将涉及在一个容器中,每次容器中作为最值的素,还要保证添加或删除素要保证能正确返回容器中作为最值的素。这正是堆结构的典型应用场景。因此哈夫曼树的构造过程应当在堆容器中进行,C++中可以使用std::priority_queue. 哈夫曼树的同权不同构 上面针对字符串”ABEBAEECCDC”生成对应的哈夫曼树的过程中,在生成树的第3步中,是将1,3两棵树合并,但是实际上,还可以将3,4两棵树合并,因为出现了多棵树的重量相同的情况。这种情况下不同的合并策略会生成不同的哈夫曼树。

 可以发现,对于上图中左边的哈夫曼树:3*1+3*2+2*3+2*3+2*4=29 对于上图中右边的哈夫曼树:2*3+2*3+3*1+3*2+2*4=29 ABCDE这5个符号对应着两套哈夫曼编码:符号频数编码1编码2AB41111C30100DE31001 即使是不同的哈夫曼树,其带权路径长度之和仍然是相等的,但某些符号的编码不相同,这种情况叫同权不同构。 实际上,采用不同的策略生成的哈夫曼树,权值相同,但对于某些符号的编码不仅有数值上的差异,还可能有长度上的差异。可能采用某种策略生成的哈夫曼树,某个符号A对应得到的哈夫曼编码为011,采用另一种策略生成的哈夫曼树符号A对应的哈夫曼编码可能就是1101了。除此之外,对给定符号的哈夫曼编码中长度最长的哈夫曼编码的长度值可能也有差异,可能这棵树的长度最长的编码为5位,另一颗树最长编码为6位。但是它们的带权路径和总是相同的,换到编码上来,编码后的数据长度总是相同的且最优。 K叉哈夫曼树 对于普通的哈夫曼树,采用二叉树生成,对应的编码是二进制的。 如果想要生成k进制的哈夫曼编码,并使得编码后的总长度最短(非二进制数据最短,而是在k进制下所需的数码个数最少),这时候就需要构建K叉哈夫曼树。 K叉哈夫曼树是除叶子节点外其他节点都有K个儿子节点的哈夫曼树,也就是节点度数为0或k。 K叉哈夫曼树在构造过程中,需要不断从森林中每次选取K个重量最小的树,合并成一棵树。每进行一次该过程,树的个数减少K-1个。这时候就会出现该过程重复到最后,剩余树的数量不足K个的情况。也就是说,如果初始状态下有N棵树,那么(N-1)不能被(K-1)整除时,就会出现剩余树的数量不足K个的情况。如果最终余下m(m<K)个树,直接将其合并成一棵树,则根据这棵树生成的编码不是最优的。这时候就需要补节点。补充M个节点,保证这M个节点的权值比原有节点都小,并保证(N+M-1)/(K-1)是整数。一般M取(K-1)-(N-1)%(K-1)即可。 由此可得K叉哈夫曼树的生成过程为: ①确定一段数据由N个不同的符号组成,计算N个不同的符号出现的频数 ②初始化N个孤立节点,也就是N个只有1个根节点的树,构成一个森林。N个节点与N个符号对应,节点的权值为对应的符号出现的频数。如果(N-1)/(K-1)不是整数,则再添加(K-1)-(N-1)%(K-1)个单节点树,保证每个新添加的树的重量都小于原有的N棵树中每棵树的重量。 ③从森林中每次选取K个重量最小的树。定义一个新节点作为父节点连接这K棵树(森林中树的个数每次减少K-1) ④重复过程③,直到只剩下一棵树(经过补点后,一定可以只剩下一棵树)。 ⑤最后一棵树便为哈夫曼树。从根节点沿着树的路径走,往每个儿子节点的方向走分别表示0,1,2,…K-1(当然也可以反过来,或者自定义符号和顺序,只要规则是确定的),即可得知对应符号的哈夫曼编码。 这里有一道K叉树模版算法题,可以用这道题来检查自己写的K叉树的正确性[NOI2015] 荷马史诗 – 洛谷 范式哈夫曼编码(Canonical Huffman Code) 通过前文可知,对于所给符号和对应频数,生成的哈夫曼树不唯一,对应的哈夫曼编码也不唯一。 如果编码一份文件给别人,别人需要解码就需要知道哈夫曼编码。 由于哈夫曼编码是针对某段数据定制的(也可以不定制,那样编码压缩的效果可能就会差点),因此通常没有事先规定好的某张标准哈夫曼编码表。即使强制采用某张编码表,对于不同数据,压缩效果不会总是很好。 可以直接存储哈夫曼编码对照表附在文件中,需要一张<编码,符号>映射表,但编码长度可能很长,导致占用更多空间;还可以确定一个统一的哈夫曼编码规则,使得生成的哈夫曼编码唯一,这就是范式哈夫曼编码。当编码规则固定时,只存储部分数据来重建编码表就成了可能。 范式哈夫曼编码(Canonical Huffman Code)最早由Schwartz提出,应用于在JPEG文件编码等领域。 个人理解,范式哈夫曼编码的核心就是编码保留位数信息,然后从头构建编码。 通过前文可知,对给定符号和对应频数生成的不同哈夫曼树,其节点的带权路径长度和总是相同且最小。而我们关心的更多是某个符号编码后具体由多少位二进制组成,至于具体的编码二进制是多少,是次要的。可能根据某个哈夫曼树得到的符号A和B的哈夫曼编码分别为1011和1110,但实际上,让A对应的编码为1110,B对应的编码为1011,完全没问题,只要不产生歧义,而且一般没必要改变他们的编码长度,因为总体编码长度已经是最优了。 范式哈夫曼编码就利用了这个思想。它确定了一些规则,只要给出一棵哈夫曼树导出的所有符号的哈夫曼编码的位数,即可唯一确定一张哈夫曼编码表。 范式哈夫曼编码的规则如下: ①编码长度最短的某一个符号的编码为全0,即编码从0开始 ②相同编码长度的符号对应的编码必须连续 ③编码长度为
可以发现,对于上图中左边的哈夫曼树:3*1+3*2+2*3+2*3+2*4=29 对于上图中右边的哈夫曼树:2*3+2*3+3*1+3*2+2*4=29 ABCDE这5个符号对应着两套哈夫曼编码:符号频数编码1编码2AB41111C30100DE31001 即使是不同的哈夫曼树,其带权路径长度之和仍然是相等的,但某些符号的编码不相同,这种情况叫同权不同构。 实际上,采用不同的策略生成的哈夫曼树,权值相同,但对于某些符号的编码不仅有数值上的差异,还可能有长度上的差异。可能采用某种策略生成的哈夫曼树,某个符号A对应得到的哈夫曼编码为011,采用另一种策略生成的哈夫曼树符号A对应的哈夫曼编码可能就是1101了。除此之外,对给定符号的哈夫曼编码中长度最长的哈夫曼编码的长度值可能也有差异,可能这棵树的长度最长的编码为5位,另一颗树最长编码为6位。但是它们的带权路径和总是相同的,换到编码上来,编码后的数据长度总是相同的且最优。 K叉哈夫曼树 对于普通的哈夫曼树,采用二叉树生成,对应的编码是二进制的。 如果想要生成k进制的哈夫曼编码,并使得编码后的总长度最短(非二进制数据最短,而是在k进制下所需的数码个数最少),这时候就需要构建K叉哈夫曼树。 K叉哈夫曼树是除叶子节点外其他节点都有K个儿子节点的哈夫曼树,也就是节点度数为0或k。 K叉哈夫曼树在构造过程中,需要不断从森林中每次选取K个重量最小的树,合并成一棵树。每进行一次该过程,树的个数减少K-1个。这时候就会出现该过程重复到最后,剩余树的数量不足K个的情况。也就是说,如果初始状态下有N棵树,那么(N-1)不能被(K-1)整除时,就会出现剩余树的数量不足K个的情况。如果最终余下m(m<K)个树,直接将其合并成一棵树,则根据这棵树生成的编码不是最优的。这时候就需要补节点。补充M个节点,保证这M个节点的权值比原有节点都小,并保证(N+M-1)/(K-1)是整数。一般M取(K-1)-(N-1)%(K-1)即可。 由此可得K叉哈夫曼树的生成过程为: ①确定一段数据由N个不同的符号组成,计算N个不同的符号出现的频数 ②初始化N个孤立节点,也就是N个只有1个根节点的树,构成一个森林。N个节点与N个符号对应,节点的权值为对应的符号出现的频数。如果(N-1)/(K-1)不是整数,则再添加(K-1)-(N-1)%(K-1)个单节点树,保证每个新添加的树的重量都小于原有的N棵树中每棵树的重量。 ③从森林中每次选取K个重量最小的树。定义一个新节点作为父节点连接这K棵树(森林中树的个数每次减少K-1) ④重复过程③,直到只剩下一棵树(经过补点后,一定可以只剩下一棵树)。 ⑤最后一棵树便为哈夫曼树。从根节点沿着树的路径走,往每个儿子节点的方向走分别表示0,1,2,…K-1(当然也可以反过来,或者自定义符号和顺序,只要规则是确定的),即可得知对应符号的哈夫曼编码。 这里有一道K叉树模版算法题,可以用这道题来检查自己写的K叉树的正确性[NOI2015] 荷马史诗 – 洛谷 范式哈夫曼编码(Canonical Huffman Code) 通过前文可知,对于所给符号和对应频数,生成的哈夫曼树不唯一,对应的哈夫曼编码也不唯一。 如果编码一份文件给别人,别人需要解码就需要知道哈夫曼编码。 由于哈夫曼编码是针对某段数据定制的(也可以不定制,那样编码压缩的效果可能就会差点),因此通常没有事先规定好的某张标准哈夫曼编码表。即使强制采用某张编码表,对于不同数据,压缩效果不会总是很好。 可以直接存储哈夫曼编码对照表附在文件中,需要一张<编码,符号>映射表,但编码长度可能很长,导致占用更多空间;还可以确定一个统一的哈夫曼编码规则,使得生成的哈夫曼编码唯一,这就是范式哈夫曼编码。当编码规则固定时,只存储部分数据来重建编码表就成了可能。 范式哈夫曼编码(Canonical Huffman Code)最早由Schwartz提出,应用于在JPEG文件编码等领域。 个人理解,范式哈夫曼编码的核心就是编码保留位数信息,然后从头构建编码。 通过前文可知,对给定符号和对应频数生成的不同哈夫曼树,其节点的带权路径长度和总是相同且最小。而我们关心的更多是某个符号编码后具体由多少位二进制组成,至于具体的编码二进制是多少,是次要的。可能根据某个哈夫曼树得到的符号A和B的哈夫曼编码分别为1011和1110,但实际上,让A对应的编码为1110,B对应的编码为1011,完全没问题,只要不产生歧义,而且一般没必要改变他们的编码长度,因为总体编码长度已经是最优了。 范式哈夫曼编码就利用了这个思想。它确定了一些规则,只要给出一棵哈夫曼树导出的所有符号的哈夫曼编码的位数,即可唯一确定一张哈夫曼编码表。 范式哈夫曼编码的规则如下: ①编码长度最短的某一个符号的编码为全0,即编码从0开始 ②相同编码长度的符号对应的编码必须连续 ③编码长度为
 的符号存在,长度为
的符号存在,长度为
 的编码中的最后一个编码
的编码中的最后一个编码
 与下一个长度
与下一个长度
 的编码
的编码
 的关系为:
的关系为:
 ,<<为二进制左移位符号。 ④编码长度为
,<<为二进制左移位符号。 ④编码长度为
 的符号存在,如果不存在编码长度为
的符号存在,如果不存在编码长度为
 的符号,直到编码长度为
的符号,直到编码长度为
 才存在对应的符号,则编码
才存在对应的符号,则编码
 与
与
 的关系为:
的关系为:
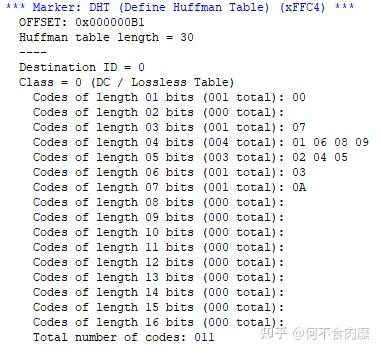
 ,<<为二进制左移位符号。 光看规则可能不好理解,下面通过一个例子来感受范式哈夫曼编码。 还是上面的ABCDE 5个符号的编码,我们已经根据哈夫曼树得到了一套编码如下:符号频数编码编码位数A21013B2002C3112D11003E3012 为了方便编码和使规律更明显,将编码对照表按照编码位数排序符号原编码位数B002E012C112D1003A1013 根据范式哈夫曼编码的规则,得到范式哈夫曼编码如下:符号原编码范式哈夫曼编码依据B0000规则①E0101规则②C1110规则②D规则③(10+1==11, 11<<1==110)A规则② 通过这种编码方法,只需要记录编码的符号对应的位数即可。 由此可见,获得范式哈夫曼编码的过程为: ①获得符号的哈夫曼编码长度信息(只保留哈夫曼编码的长度信息,舍弃符号对应编码的二进制值) ②依据范式哈夫曼编码规则,重新赋予符号编码 假设我们只知道如下信息:符号编码长度B2E2C2D3A3 我们可以反推编码:符号编码长度范式哈夫曼编码依据B200规则①(编码总是从最短位全0开始)E201规则②(同一编码长度下要连续)C210规则②(同一编码长度下要连续)D3110规则③(10+1==11,11<<1==110)A3111规则②(同一编码长度下要连续) 这样,只需要存储符号和编码长度对照表,即可得知范式哈夫曼编码,不必存储范式哈夫曼编码本身了。 下面是从某张JPEG图片中解析出的哈夫曼表,该表只含有编码长度和符号信息,需要依据范式哈夫曼编码规则反推其编码
,<<为二进制左移位符号。 光看规则可能不好理解,下面通过一个例子来感受范式哈夫曼编码。 还是上面的ABCDE 5个符号的编码,我们已经根据哈夫曼树得到了一套编码如下:符号频数编码编码位数A21013B2002C3112D11003E3012 为了方便编码和使规律更明显,将编码对照表按照编码位数排序符号原编码位数B002E012C112D1003A1013 根据范式哈夫曼编码的规则,得到范式哈夫曼编码如下:符号原编码范式哈夫曼编码依据B0000规则①E0101规则②C1110规则②D规则③(10+1==11, 11<<1==110)A规则② 通过这种编码方法,只需要记录编码的符号对应的位数即可。 由此可见,获得范式哈夫曼编码的过程为: ①获得符号的哈夫曼编码长度信息(只保留哈夫曼编码的长度信息,舍弃符号对应编码的二进制值) ②依据范式哈夫曼编码规则,重新赋予符号编码 假设我们只知道如下信息:符号编码长度B2E2C2D3A3 我们可以反推编码:符号编码长度范式哈夫曼编码依据B200规则①(编码总是从最短位全0开始)E201规则②(同一编码长度下要连续)C210规则②(同一编码长度下要连续)D3110规则③(10+1==11,11<<1==110)A3111规则②(同一编码长度下要连续) 这样,只需要存储符号和编码长度对照表,即可得知范式哈夫曼编码,不必存储范式哈夫曼编码本身了。 下面是从某张JPEG图片中解析出的哈夫曼表,该表只含有编码长度和符号信息,需要依据范式哈夫曼编码规则反推其编码

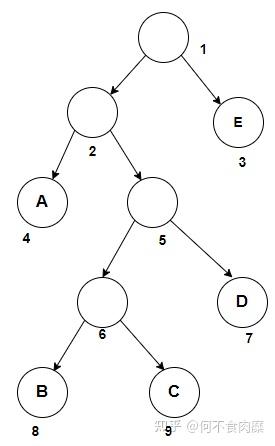
 下面是反推过程:符号编码位数范式哈夫曼编码依据0010规则①073100规则④(0+1==1,1<<2==100)0规则③(100+1=101,101<<1==1010)0规则②0规则②0规则②0规则③(1101+1=1110,1110<<1==11100)0规则②0规则②0规则③(11110+1=11111,11111<<1==)0A规则③(+1=,<<1==) 可见如果将符号对应的编码也存储起来,则需要多存储48bit,实际上,这是表比较小的情况下, 如果表中的符号多达几百个,则需要多存储的信息将更多。范式哈夫曼编码可以起到压缩编码表的作用。 范式哈夫曼编码就是依据某个符号-编码长度表生成对应编码的方法。此时哈夫曼树是一种每个符号的编码长度的工具,而非具体编码的工具。符号-编码长度表通过构造哈夫曼树得到,而编码通过范式哈夫曼编码算法得到。 哈夫曼编码位数的限制方法 在某些情况下,我们需要限制单个符号的哈夫曼编码位数,例如在JPEG文件中,某个符号的哈夫曼编码长度最大为16bit,超过16bit部分需要通过一定方法,在保证不产生歧义的情况下,同时保证编码能使得数据长度尽可能短,将其强行赋予一个16bit长度及以下的编码。下文记录了一种限制方法。 符号-编码长度表和哈夫曼树具有以下关系和特征: ①节点所在的深度决定了符号对应编码的长度 ②符号所在的节点一定是叶子节点 ③节点如果是非叶子节点,则一定有左右两个儿子 ④叶子节点数目与要编码的符号数目相同 限制编码的长度实际上就是限制树的最大深度。这时候,只能对哈夫曼树做手脚。 首先,要保证树的叶子节点树不变,这里设叶子节点数为n。 根据哈夫曼树的特征③,我们每次选择2个深度较大的节点A,B,设它们的深度为i。它们具有共同的父节点C,深度为i-1,将其与父节点分离,此时产生了一个深度为i-1的叶子节点C,树的叶子节点数变成了n-1。 现在再选择某个深度较小(设深度为j,j<i-1)的叶子节点D,作为父节点承接刚刚分离出来的2个节点。节点D由叶子节点变为非叶子节点,原来被分离出去的深度为i节点A,B,变成了深度为j+1的两个叶子节点A,B,树的叶子节点数恢复成n. 整个过程中: ①超出深度限制的叶子节点A,B,由深度i变成了深度j+1(j+1<i); ②产生了一个深度为i-1的新叶子节点C,该节点为节点A,B的旧父节点; ③失去了一个深度为j的叶子节点D,该节点为节点A,B的新父节点。 ④原来的叶子节点深度顺序:A=B>D,新的叶子节点深度顺序: A=B<=C ⑤节点D的选择可以采用贪心方法,即深度较深的优先选为节点D ⑥深度为i的叶子节点个数减少了2个,深度为i-1的叶子节点个数增加了1个,深度为j+1的叶子节点个数增加了2个,深度为j的叶子节点个数减少了1个 ⑦重复上面的过程可以将编码限制在某个长度内 可见新的树的编码不再是最优的,而是以延长整体编码长度为代价限制了部分符号的编码长度。 而且,不能简单地不改变原来的节点-符号对应关系,从上面的过程可知,原来的叶子节点为A,B,D,A,B最深,而新的叶子节点为A,B,C,C的深度可能比A,B更深,如果此时直接将节点D对应的符号绑定到C上,则最终的编码长度会更长。因此应该将原来的A,B对应的2个符号中频数更低的绑定到D上, 原来B,C对应的符号绑定的新的节点A,B上。 只看文字可能很难理解,下面用一个例子模拟这个过程 假设这是一棵哈夫曼树
下面是反推过程:符号编码位数范式哈夫曼编码依据0010规则①073100规则④(0+1==1,1<<2==100)0规则③(100+1=101,101<<1==1010)0规则②0规则②0规则②0规则③(1101+1=1110,1110<<1==11100)0规则②0规则②0规则③(11110+1=11111,11111<<1==)0A规则③(+1=,<<1==) 可见如果将符号对应的编码也存储起来,则需要多存储48bit,实际上,这是表比较小的情况下, 如果表中的符号多达几百个,则需要多存储的信息将更多。范式哈夫曼编码可以起到压缩编码表的作用。 范式哈夫曼编码就是依据某个符号-编码长度表生成对应编码的方法。此时哈夫曼树是一种每个符号的编码长度的工具,而非具体编码的工具。符号-编码长度表通过构造哈夫曼树得到,而编码通过范式哈夫曼编码算法得到。 哈夫曼编码位数的限制方法 在某些情况下,我们需要限制单个符号的哈夫曼编码位数,例如在JPEG文件中,某个符号的哈夫曼编码长度最大为16bit,超过16bit部分需要通过一定方法,在保证不产生歧义的情况下,同时保证编码能使得数据长度尽可能短,将其强行赋予一个16bit长度及以下的编码。下文记录了一种限制方法。 符号-编码长度表和哈夫曼树具有以下关系和特征: ①节点所在的深度决定了符号对应编码的长度 ②符号所在的节点一定是叶子节点 ③节点如果是非叶子节点,则一定有左右两个儿子 ④叶子节点数目与要编码的符号数目相同 限制编码的长度实际上就是限制树的最大深度。这时候,只能对哈夫曼树做手脚。 首先,要保证树的叶子节点树不变,这里设叶子节点数为n。 根据哈夫曼树的特征③,我们每次选择2个深度较大的节点A,B,设它们的深度为i。它们具有共同的父节点C,深度为i-1,将其与父节点分离,此时产生了一个深度为i-1的叶子节点C,树的叶子节点数变成了n-1。 现在再选择某个深度较小(设深度为j,j<i-1)的叶子节点D,作为父节点承接刚刚分离出来的2个节点。节点D由叶子节点变为非叶子节点,原来被分离出去的深度为i节点A,B,变成了深度为j+1的两个叶子节点A,B,树的叶子节点数恢复成n. 整个过程中: ①超出深度限制的叶子节点A,B,由深度i变成了深度j+1(j+1<i); ②产生了一个深度为i-1的新叶子节点C,该节点为节点A,B的旧父节点; ③失去了一个深度为j的叶子节点D,该节点为节点A,B的新父节点。 ④原来的叶子节点深度顺序:A=B>D,新的叶子节点深度顺序: A=B<=C ⑤节点D的选择可以采用贪心方法,即深度较深的优先选为节点D ⑥深度为i的叶子节点个数减少了2个,深度为i-1的叶子节点个数增加了1个,深度为j+1的叶子节点个数增加了2个,深度为j的叶子节点个数减少了1个 ⑦重复上面的过程可以将编码限制在某个长度内 可见新的树的编码不再是最优的,而是以延长整体编码长度为代价限制了部分符号的编码长度。 而且,不能简单地不改变原来的节点-符号对应关系,从上面的过程可知,原来的叶子节点为A,B,D,A,B最深,而新的叶子节点为A,B,C,C的深度可能比A,B更深,如果此时直接将节点D对应的符号绑定到C上,则最终的编码长度会更长。因此应该将原来的A,B对应的2个符号中频数更低的绑定到D上, 原来B,C对应的符号绑定的新的节点A,B上。 只看文字可能很难理解,下面用一个例子模拟这个过程 假设这是一棵哈夫曼树

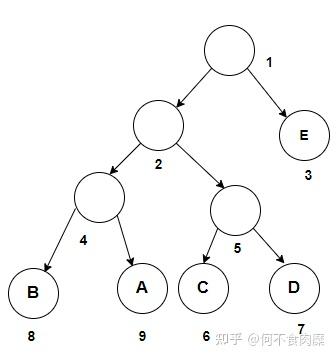
 我们可以得到该树导出的符号-编码长度表符号编码长度范式哈夫曼编码E10A210D3110B41110C41111 现在,某程序设计提出一个要求:符号的编码长度不得大于3 以上面的树为例,我们注意到在第三层有个叶子节点4,如果将8、9两个节点转移到4节点上,将4节点作为父节点,而8、9两个节点在转移后恰好在第三层又产生了一个新节点,这时候就成功限制了符号的编码长度不得大于3。新的树和编码结果如下:
我们可以得到该树导出的符号-编码长度表符号编码长度范式哈夫曼编码E10A210D3110B41110C41111 现在,某程序设计提出一个要求:符号的编码长度不得大于3 以上面的树为例,我们注意到在第三层有个叶子节点4,如果将8、9两个节点转移到4节点上,将4节点作为父节点,而8、9两个节点在转移后恰好在第三层又产生了一个新节点,这时候就成功限制了符号的编码长度不得大于3。新的树和编码结果如下:

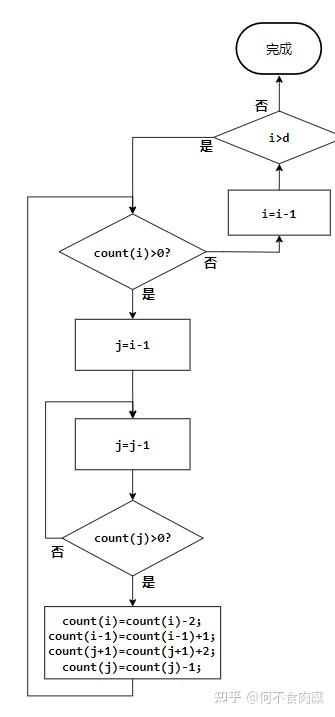
 符号编码长度范式哈夫曼编码E10B3100A3101C3110D3111 虽然上面的操作是基于树的节点增删操作,但是可以不直接对树进行操作。根据前面给出的限制过程,树的节点增删操作最终会造成对应深度的叶子节点个数的变化,而编码长度与对应树的叶子节点的深度对应。因此统计出不同编码长度的符号个数,直接针对个数进行修正(可以通过结构体等方法保证修正后的符号-编码长度对应关系),修正后再走一轮范式哈夫曼编码,即可起到限制符号编码长度的作用。流程如下,其中count(i)表示编码长度为i的符号个数:
符号编码长度范式哈夫曼编码E10B3100A3101C3110D3111 虽然上面的操作是基于树的节点增删操作,但是可以不直接对树进行操作。根据前面给出的限制过程,树的节点增删操作最终会造成对应深度的叶子节点个数的变化,而编码长度与对应树的叶子节点的深度对应。因此统计出不同编码长度的符号个数,直接针对个数进行修正(可以通过结构体等方法保证修正后的符号-编码长度对应关系),修正后再走一轮范式哈夫曼编码,即可起到限制符号编码长度的作用。流程如下,其中count(i)表示编码长度为i的符号个数:

 上面的流程显示,当检测到存在超出限制编码长度d的符号时(编码长度设为i),寻找比i-1更小且存在的编码长度存在,这一过程实际上就相当于前面的在树中选择某个深度较小(设深度为j,j<i-1)的叶子节点D 找到后 这四个步骤实际上就是对标前面提到的过程⑥:深度为i的叶子节点个数减少了2个,深度为i-1的叶子节点个数增加了1个,深度为j+1的叶子节点个数增加了2个,深度为j的叶子节点个数减少了1个。 因此,如果有需要对哈夫曼编码位数限制的需求,则可以通过下面的过程获得范式哈夫曼编码: ①准备好待编码符号的符号-频数表 ②构建哈夫曼树各个符号的编码长度信息 ③计算每个长度i的编码个数count(i) ④通过操作count(i)数组模拟“在树上增删节点”的操作 ⑤根据符号-频数表和count(i)数组和范式哈夫曼编码规则构建编码(频数小的先占用长编码,频数大的占用短编码) 注:上面的哈夫曼编码位数限制算法参考了ITU-T81标准中给出的方法
上面的流程显示,当检测到存在超出限制编码长度d的符号时(编码长度设为i),寻找比i-1更小且存在的编码长度存在,这一过程实际上就相当于前面的在树中选择某个深度较小(设深度为j,j<i-1)的叶子节点D 找到后 这四个步骤实际上就是对标前面提到的过程⑥:深度为i的叶子节点个数减少了2个,深度为i-1的叶子节点个数增加了1个,深度为j+1的叶子节点个数增加了2个,深度为j的叶子节点个数减少了1个。 因此,如果有需要对哈夫曼编码位数限制的需求,则可以通过下面的过程获得范式哈夫曼编码: ①准备好待编码符号的符号-频数表 ②构建哈夫曼树各个符号的编码长度信息 ③计算每个长度i的编码个数count(i) ④通过操作count(i)数组模拟“在树上增删节点”的操作 ⑤根据符号-频数表和count(i)数组和范式哈夫曼编码规则构建编码(频数小的先占用长编码,频数大的占用短编码) 注:上面的哈夫曼编码位数限制算法参考了ITU-T81标准中给出的方法
2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。
文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/35937.html