一篇搞定红黑树:从原理到应用实战 前言:红黑树是一种自平衡二叉查找树,是在计算机科学中用到的一种数据结构,典型的用途是实现关联数组。它是在1972年由鲁道夫·贝尔发明的,他称之为”对称二叉B树”,它现代的名字是在 Leo J.Guibas 和Robert Sedgewick于1978年写的一篇论文中获得的。它是复杂的,但它的操作有着良好的最坏情况运行时间,并且在实践中是高效的: 它可以在O(logn)时间内做查找,插入和删除,这里的n是树中素的数目。 精品文章推荐:C/C++发展方向(强烈推荐!!)Linux C/C++开发上线项目(后端、音视频、存储、QT)2023年Linux的知识技术合集(基础入门到高级进阶)2023年C/C++高性能技术知识大整理(进阶到大神级别)2023年音视频开发知识技术合集(基础入门到高级进阶) 一、红黑树的概念 红黑树,是一种二叉搜索树,但在每个节点上增加一个存储位表示节点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个节点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。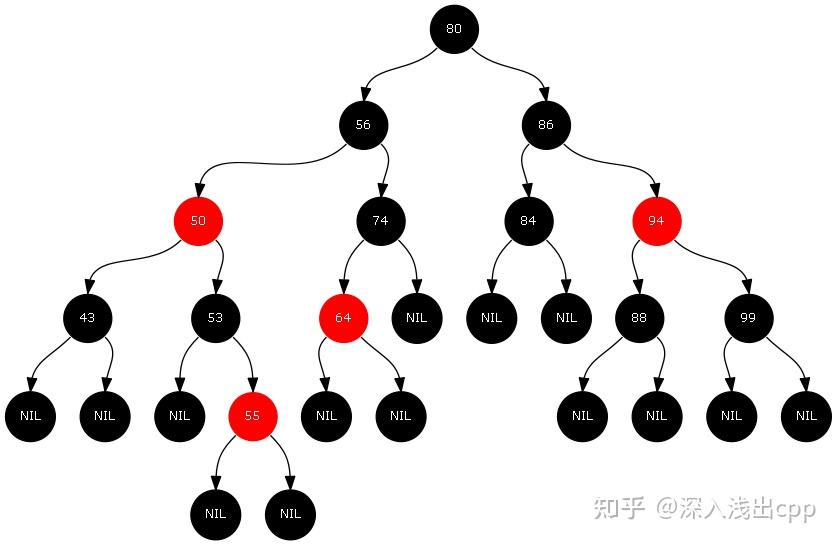




2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/33790.html