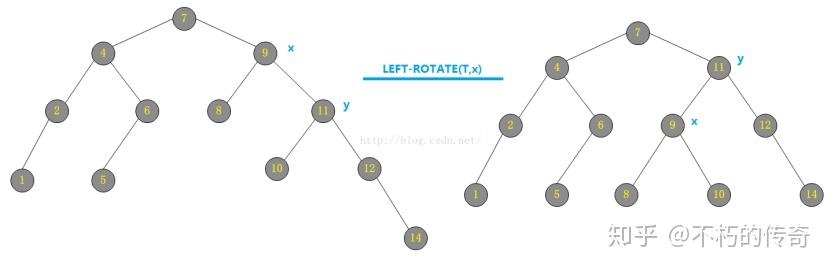
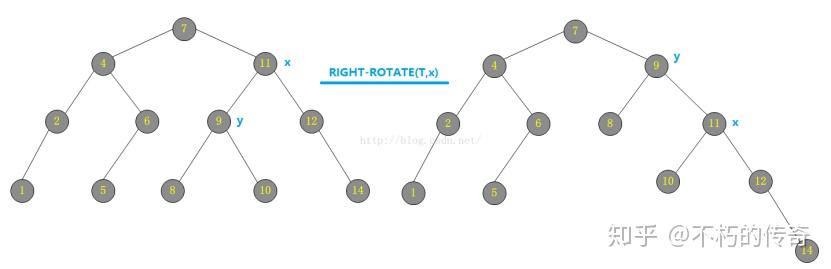
备战秋招——算法与数据结构(1) ● 请你来说一说红黑树和AVL树的定义,特点,以及二者区别 参考回答: 平衡二叉树(AVL树): 平衡二叉树又称为AVL树,是一种特殊的二叉排序树。其左右子树都是平衡二叉树,且左右子树高度之差的绝对值不超过1。一句话表述为:以树中所有结点为根的树的左右子树高度之差的绝对值不超过1。将二叉树上结点的左子树深度减去右子树深度的值称为平衡因子BF,那么平衡二叉树上的所有结点的平衡因子只可能是-1、0和1。只要二叉树上有一个结点的平衡因子的绝对值大于1,则该二叉树就是不平衡的。 红黑树: 红黑树是一种二叉查找树,但在每个节点增加一个存储位表示节点的颜色,可以是红或黑(非红即黑)。通过对任何一条从根到叶子的路径上各个节点着色的方式的限制,红黑树确保没有一条路径会比其它路径长出两倍,因此,红黑树是一种弱平衡二叉树,相对于要求严格的AVL树来说,它的旋转次数少,所以对于搜索,插入,删除操作较多的情况下,通常使用红黑树。 性质: 1. 每个节点非红即黑 2. 根节点是黑的; 3. 每个叶节点(叶节点即树尾端NULL指针或NULL节点)都是黑的; 4. 如果一个节点是红色的,则它的子节点必须是黑色的。 5. 对于任意节点而言,其到叶子点树NULL指针的每条路径都包含相同数目的黑节点; 区别: AVL 树是高度平衡的,频繁的插入和删除,会引起频繁的rebalance,导致效率下降;红黑树不是高度平衡的,算是一种折中,插入最多两次旋转,删除最多三次旋转。 ● 请你说一下哈夫曼编码 参考回答: 哈夫曼编码是哈夫曼树的一种应用,广泛用于数据文件压缩。哈夫曼编码算法用字符在文件中出现的频率来建立使用0,1表示个字符的最优表示方式,其具体算法如下: (1)哈夫曼算法以自底向上的方式构造表示最优前缀码的二叉树T。 (2)算法以|C|个叶结点开始,执行|C|-1次的“合并”运算后产生最终所要求的树T。 (3)假设编码字符集中每一字符c的频率是f(c)。以f为键值的优先队列Q用在贪心选择时有效地确定算法当前要合并的2棵具有最小频率的树。一旦2棵具有最小频率的树合并后,产生一棵新的树,其频率为合并的2棵树的频率之和,并将新树插入优先队列Q。经过n-1次的合并后,优先队列中只剩下一棵树,即所要求的树T。 ● 请你回答一下map底层为什么用红黑树实现 参考回答: 1、红黑树: 红黑树是一种二叉查找树,但在每个节点增加一个存储位表示节点的颜色,可以是红或黑(非红即黑)。通过对任何一条从根到叶子的路径上各个节点着色的方式的限制,红黑树确保没有一条路径会比其它路径长出两倍,因此,红黑树是一种弱平衡二叉树,相对于要求严格的AVL树来说,它的旋转次数少,所以对于搜索,插入,删除操作较多的情况下,通常使用红黑树。 性质: 1. 每个节点非红即黑 2. 根节点是黑的; 3. 每个叶节点(叶节点即树尾端NULL指针或NULL节点)都是黑的; 4. 如果一个节点是红色的,则它的子节点必须是黑色的。 5. 对于任意节点而言,其到叶子点树NULL指针的每条路径都包含相同数目的黑节点; 2、平衡二叉树(AVL树): 红黑树是在AVL树的基础上提出来的。 平衡二叉树又称为AVL树,是一种特殊的二叉排序树。其左右子树都是平衡二叉树,且左右子树高度之差的绝对值不超过1。 AVL树中所有结点为根的树的左右子树高度之差的绝对值不超过1。 将二叉树上结点的左子树深度减去右子树深度的值称为平衡因子BF,那么平衡二叉树上的所有结点的平衡因子只可能是-1、0和1。只要二叉树上有一个结点的平衡因子的绝对值大于1,则该二叉树就是不平衡的。 3、红黑树较AVL树的优点: AVL 树是高度平衡的,频繁的插入和删除,会引起频繁的rebalance,导致效率下降;红黑树不是高度平衡的,算是一种折中,插入最多两次旋转,删除最多三次旋转。 所以红黑树在查找,插入删除的性能都是O(logn),且性能稳定,所以STL里面很多结构包括map底层实现都是使用的红黑树。 ● 请你介绍一下B+树 参考回答: B+是一种多路搜索树,主要为磁盘或其他直接存取辅助设备而设计的一种平衡查找树,在B+树中,每个节点的可以有多个孩子,并且按照关键字大小有序排列。所有记录节点都是按照键值的大小顺序存放在同一层的叶节点中。相比B树,其具有以下几个特点: 每个节点上的指针上限为2d而不是2d+1(d为节点的出度) 内节点不存储data,只存储key 叶子节点不存储指针 ● 请你说一说map和unordered_map的底层实现 参考回答: map底层是基于红黑树实现的,因此map内部素排列是有序的。而unordered_map底层则是基于哈希表实现的,因此其素的排列顺序是杂乱无序的。 ● 请你回答一下map和unordered_map优点和缺点 参考回答: 对于map,其底层是基于红黑树实现的,优点如下: 1)有序性,这是map结构最大的优点,其素的有序性在很多应用中都会简化很多的操作 2)map的查找、删除、增加等一系列操作时间复杂度稳定,都为logn 缺点如下: 1)查找、删除、增加等操作平均时间复杂度较慢,与n相关 对于unordered_map来说,其底层是一个哈希表,优点如下: 查找、删除、添加的速度快,时间复杂度为常数级O(c) 缺点如下: 因为unordered_map内部基于哈希表,以(key,value)对的形式存储,因此空间占用率高 Unordered_map的查找、删除、添加的时间复杂度不稳定,平均为O(c),取决于哈希函数。极端情况下可能为O(n) ● 请你回答一下epoll怎么实现的 参考回答: Linux epoll机制是通过红黑树和双向链表实现的。 首先通过epoll_create()系统调用在内核中创建一个eventpoll类型的句柄,其中包括红黑树根节点和双向链表头节点。然后通过epoll_ctl()系统调用,向epoll对象的红黑树结构中添加、删除、修改感兴趣的事件,返回0标识成功,返回-1表示失败。最后通过epoll_wait()系统调用判断双向链表是否为空,如果为空则阻塞。当文件描述符状态改变,fd上的回调函数被调用,该函数将fd加入到双向链表中,此时epoll_wait函数被唤醒,返回就绪好的事件。 ● 请你说一说Top(K)问题 参考回答: 1、直接全部排序(只适用于内存够的情况) 当数据量较小的情况下,内存中可以容纳所有数据。则最简单也是最容易想到的方法是将数据全部排序,然后取排序后的数据中的前K个。 这种方法对数据量比较敏感,当数据量较大的情况下,内存不能完全容纳全部数据,这种方法便不适应了。即使内存能够满足要求,该方法将全部数据都排序了,而题目只要求找出top K个数据,所以该方法并不十分高效,不建议使用。 2、快速排序的变形 (只使用于内存够的情况) 这是一个基于快速排序的变形,因为第一种方法中说到将所有素都排序并不十分高效,只需要找出前K个最大的就行。 这种方法类似于快速排序,首先选择一个划分,将比这个划分大的素放到它的前面,比划分小的素放到它的后面,此时完成了一趟排序。如果此时这个划分的序号index刚好等于K,那么这个划分以及它左边的数,刚好就是前K个最大的素;如果index > K,那么前K大的数据在index的左边,那么就继续递归的从index-1个数中进行一趟排序;如果index < K,那么再从划分的右边继续进行排序,直到找到序号index刚好等于K为止。再将前K个数进行排序后,返回Top K个素。这种方法就避免了对除了Top K个素以外的数据进行排序所带来的不必要的开销。 3、最小堆法 这是一种局部淘汰法。先读取前K个数,建立一个最小堆。然后将剩余的所有数字依次与最小堆的堆顶进行比较,如果小于或等于堆顶数据,则继续比较下一个;否则,删除堆顶素,并将新数据插入堆中,重新调整最小堆。当遍历完全部数据后,最小堆中的数据即为最大的K个数。 4、分治法 将全部数据分成N份,前提是每份的数据都可以读到内存中进行处理,找到每份数据中最大的K个数。此时剩下N*K个数据,如果内存不能容纳N*K个数据,则再继续分治处理,分成M份,找出每份数据中最大的K个数,如果M*K个数仍然不能读到内存中,则继续分治处理。直到剩余的数可以读入内存中,那么可以对这些数使用快速排序的变形或者归并排序进行处理。 5、Hash法 如果这些数据中有很多重复的数据,可以先通过hash法,把重复的数去掉。这样如果重复率很高的话,会减少很大的内存用量,从而缩小运算空间。处理后的数据如果能够读入内存,则可以直接排序;否则可以使用分治法或者最小堆法来处理数据。 ● 请你说一说C++两种map 参考回答: unordered_map(哈希表)和map(红黑树) ● 请你说一说红黑树的性质还有左右旋转 参考回答: 考察点:算法 公司:京东,阿里巴巴 1)平衡二叉树(AVL树): 红黑树是在AVL树的基础上提出来的。 平衡二叉树又称为AVL树,是一种特殊的二叉排序树。其左右子树都是平衡二叉树,且左右子树高度之差的绝对值不超过1。 AVL树中所有结点为根的树的左右子树高度之差的绝对值不超过1。 将二叉树上结点的左子树深度减去右子树深度的值称为平衡因子BF,那么平衡二叉树上的所有结点的平衡因子只可能是-1、0和1。只要二叉树上有一个结点的平衡因子的绝对值大于1,则该二叉树就是不平衡的。 2)红黑树: 红黑树是在AVL树的基础上发展而来的。红黑树是一种二叉查找树,但在每个节点增加一个存储位表示节点的颜色,可以是红或黑(非红即黑)。通过对任何一条从根到叶子的路径上各个节点着色的方式的限制,红黑树确保没有一条路径会比其它路径长出两倍,因此,红黑树是一种弱平衡二叉树,相对于要求严格的AVL树来说,它的旋转次数少,所以对于搜索,插入,删除操作较多的情况下,通常使用红黑树。 性质: 1. 每个节点非红即黑 2. 根节点是黑的; 3. 每个叶节点(叶节点即树尾端NULL指针或NULL节点)都是黑的; 4. 如果一个节点是红色的,则它的子节点必须是黑色的。 5. 对于任意节点而言,其到叶子点树NULL指针的每条路径都包含相同数目的黑节点; 从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。它可以在O(log n)时间内做查找,插入和删除,这里的n 是树中素的数目。恢复红黑属性需要少量(O(log n))的颜色变更(这在实践中是非常快速的)并且不超过三次树旋转(对于插入是两次)。这允许插入和删除保持为 O(log n) 次,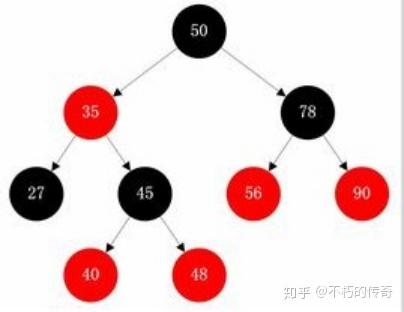
2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/31149.html