求不定积分的又一件利器，分部积分法的分析与应用 分部积分法是除了换积分法之外的另一种重要的求不定积分的方法。它是基于下面的定理的： 定理：(分部积分法)若u(x)与v(x)可导，∫u’(x)v(x)dx存在， 则∫u(x)v’(x)dx也存在，并有∫u(x)v’(x)dx=u(x)v(x)-∫u’(x)v(x)dx. 可简写为：∫udv=uv-∫vdu. (分部积分公式) 之所以有最后的简写形式，是因为v’dx=dv, u’dx=du. 这其实是一个凑微分的过程，所以运用分部积分法时，常常可以看到有一个凑微分的步骤。有人可能会说，这不就是换一个函数求导吗？有什么用呢？别急，老黄先给大家证明这个定理，一会儿用例题来说明它的用处。 证：由(u(x)v(x))’=u’(x)v(x)+u(x)v’(x)，得【运用了积的求导法则】 ∫(u(x)v(x))’dx=∫[u’(x)v(x)+u(x)v’(x)]dx =∫u’(x)v(x)dx+∫u(x)v’(x)dx，【运用了和的积分等于积分的和的公式】 即有∫u(x)v’(x)dx=∫(u(x)v(x))’dx-∫u’(x)v(x)dx =u(x)v(x)-∫u’(x)v(x)dx.【这里利用了求导和求不定积分的互逆性。不知道你有没有想过，这里好象丢了一个C。导数的不定积分应该有个常数C的。其实没丢，不要紧张，放松点，这个C还在后面的不定积分里。把后面的不定积分求出来，C自然就会出来了】 
接下来我们来看运用。 例1：∫xcosxdx. 想一想，如果不用分部积分法，你能用其它方法求这个不定积分吗？有可能可以，但是会很麻烦。用分部积分法就会很容易。观察不难发现，这个不定积分和正弦的不定积分会有一定的联系，因此我们可以先把cosxdx凑微分成dsinx的形式，从而得到∫xdsinx。注意右边这个形式，如果把它看作分部积分公式的左边的形式，你会怎么确定u和v呢？ 解：∵∫sinxdx=-cosx+C， ∴∫xcosxdx=∫xdsinx=∫udv=uv-∫vdu =xsinx-∫sinxdx=xsinx+cosx+C. 
例2：求∫arctanxdx. 不用分部积分法，你能求吗？很难，那么如果直接对它运用分部积分法，会怎么样呢？根据分部积分公式，可以有u=arctanx, v=x，而du=darctanx是可以求微分的，直接运用公式，就可以解决这个问题了。 解：∵∫xd(arctanx)=∫x/(x^2+1)dx =1/2* ∫1/(x^2+1)* d(x^2+1)=1/2*ln(x^2+1)+C，【这里结合了第一换积分法】 ∴∫arctanxdx=xarctanx-∫xd(arctanx) =xarctanx- 1/2*ln(x^2+1)+C. 
现在你能自己解决下面的练习题吗？ 练习：求∫arcsinxdx 解：∵∫xd(arcsinx)=∫x/√(1-x^2 )dx=-√(1-x^2 ) ， ∴∫arcsinxdx=xarcsinx-∫xd(arcsinx) =xarcsinx-√(1-x^2 )+C. 
怎么样？你有没有感觉自己爱上这种求积分的方法了。分部积分法，一定要多加练习哦，和换积分法结合起来，就可以解决大多数不定积分了。
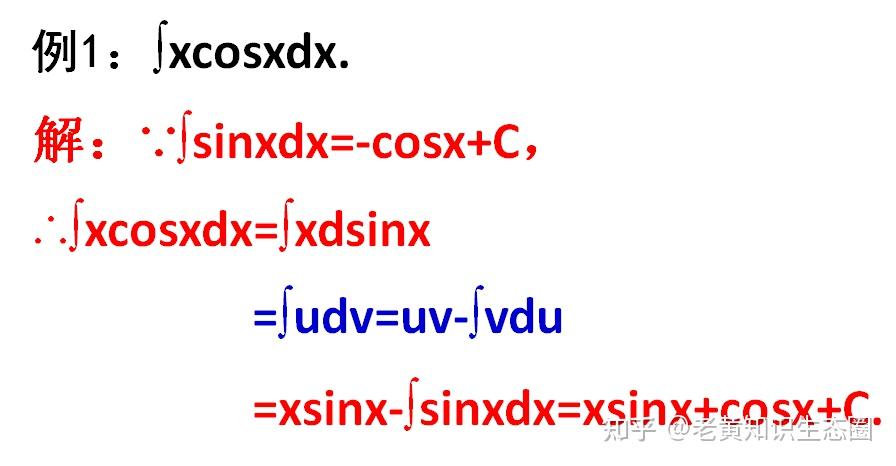
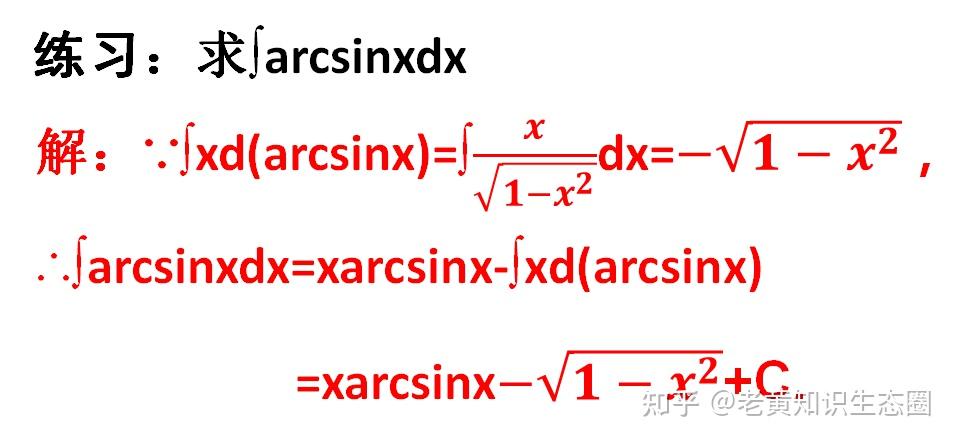
2024最新激活全家桶教程，稳定运行到2099年，请移步至置顶文章：https://sigusoft.com/99576.html
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请联系我们举报，一经查实，本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处：https://sigusoft.com/29039.html
