永磁同步电机控制&FOC驱动 本文首先对永磁同步电机(PMSM)进行了数学建模,基于磁场定向控制方法建立了磁链方程、电压方程和力矩方程,并在之后搭建了Simulink模型,作为后续多轮协调控制的仿真框图之一。接着,基于电机磁场定向控制的原理,实现了FOC控制算法,并在已有硬件上进行了调试,能够正常运行,为之后控制算法的部署打下基础。 //本文PMSM建模部分主要参考自[1] 如何快速理解永磁同步电机? PMSM数学模型 故事可以从电流的磁效应讲起:奥斯特-发现电流的磁效应;磁场强度的单位是O。1820年7月发表电流的磁效的文章,所以一开始的磁场强度是和电流强度挂钩的一个量。安培定理:在恒定电流的磁场中,磁场强度 H矢量 沿任何闭合路径 C (即环路积分)的线积分等于其所包围的电流强度的代数






































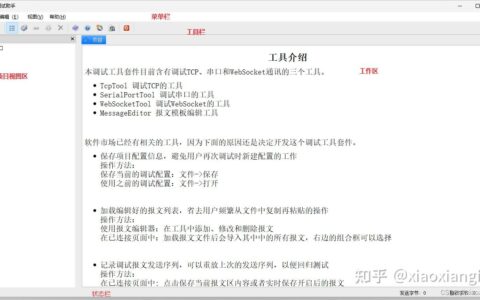
![matlab左移函数_matlab与运算插图89 \vec{T}=p\cdot\vec{\Psi_s}\times\vec{i_s}=p\left( \Psi_di_q-\Psi_qi_d \right)=p\left[ \Psi_mi_q+(L_d-L_q)i_di_q \right]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)





































2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/27981.html