【计算机组成原理】定点数的移位运算 移码表示法 Q：为什么要叫做移码呢？ A：移码常用来表示浮点数的阶码。它只能表示整数。 移码就是在真值X上加上一个常数（偏置值），通常这个常数取2n，相当于X在数轴上向正方向偏移了若干单位，这就是“移码”一词的由来。 Q：那移码又是什么呢？ A：移码定义为[x]移= 2n+x（其中x大于等于-2n，小于2n；机器字长为n+1） 阶码的定义： 我们之前了解的原码，反码和补码都是针对定点数而言，而移码常用于表示浮点数的阶码。相信一些同学对于阶码的概念还有些陌生：所谓阶码是指在机器中表示一个浮点数时需要给出指数，这个指数用整数形式表示，这个整数叫做阶码，阶码指明了小数点在数据中的位置。当阶码为固定值时，数的这种表示法称为定点表示，这样的数称为“定点数”；当阶码为可变时，数的这种表示法称为浮点表示，这样的数称为“浮点数”。 那现在用例子来解释移码的定义：若正数x1=+10101，x2=-10101，字长为8位，则移码表示为:[x1]移=27+10101=1,0010101；[x2]移=27+(-10101)=0,。 移码的特点： 1）移码中零的表示唯一。 2）一个真值的移码和补码仅差一个符号位，[x]补的符号位取反即得[x]移（“1”表示正，“0”表示负，这与其他机器数符号位取值正好相反），反之亦然。 3）移码全0时，对应真值最小值-2n；移码全1时，对应真值的最大值2n-1。 4）移码保持数据原有大小顺序，移码大真值就大，移码小真值就小。 定点数的移位运算 学习了原码，补码，反码，移码的概念，当然还是要应用起来啦！我们主要应用原码，补码，反码进行移位运算，加减运算，乘除运算。现在就从最简单的移位运算开始吧！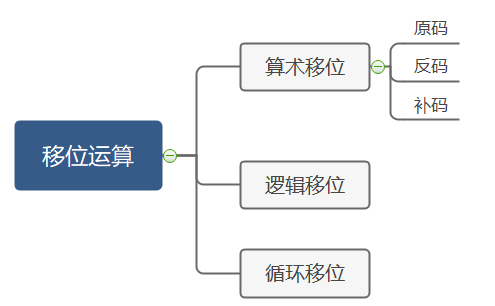
通过思维导图我们可以看到移位运算主要分为算术移位，逻辑移位和循环移位三种方式：有符号数的移位称为算术移位，逻辑移位的操作对象是逻辑代码，可以视为无符号数，我们就依次来了解学习。 算术移位 ※ 算术移位的对象是有符号数，在移位过程中符号位保持不变。 ※ 我们知道正数的原码，补码，反码与真值相同，即[x]原=[x]补=[x]反=真值，因此移位后出现的空位均以0添之。 ※ 对于负数，由于原码、补码、反码的表示形式不同，因此当机器数移位时，对其空位的添补规则也不同。
这里我们需要注意：不论是正数还是负数，移位后其符号位均不变！ 这里我们用原码的算术移位给大家演示一下负数的算术移位：
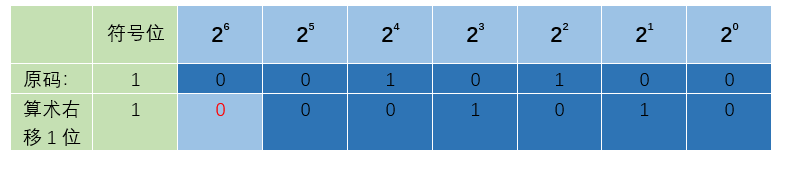可以看出在进行算术右移时符号位是没有移动的，深蓝色的代表数值位，数值位就依次右移一位，然后空余的位被填充为0。 逻辑移位 ※ 逻辑移位将操作数视为无符号数，移位规则：逻辑左移时，高位移丢，低位添0；逻辑右移时，低位移丢，高位添0。 ※ 注意：逻辑移位不管是左移还是右移，都添0。
循环移位 ※ 循环移位分为带进位标志位CF的循环移位（大循环）和不带进位标志位的循环移位（小循环)。 ※ 循环移位的主要特点是，移出的数位又被移入数据中，而是否带进位则要看是否将进位标志位加入循环位移。例如，带进位位的循环左移就是数据位连同进位标志位一起左移，数据的最高位移入进位标志位CF，而进位位则依次移入数据的最低位。 相信大家也发现了一个问题：算术移位和逻辑移位中不管是左移还是右移，原始数值位都会有二进制数被移出丢弃。但循环移位的二进制数在移位过程中不丢弃，这也使循环移位操作特别适合将数据的低字节数据和高字节数据互换。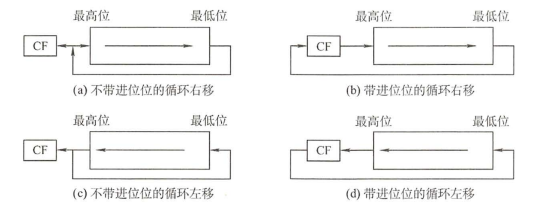
最后通过题目来巩固下知识吧！ 1.补码定点整数0101 0101左移两位后的值为（)。 A. 0100 0111 B. 0 C. 0100 0110 D. 0101 0101 解析： 我们可以发现这个补码定点整数符号位为0，得知是正数，根据算术补码移位规则，正数左右移位都添0，符号位不变。 2.补码定点整数右移一位后的值为（)。 A. 0100 1010 B. 0100 1010 1 C. 1000 1010 D. 1100 1010 解析： 现在补码符号位为1，得知是负数，根据算术补码移位规则，负数右移添1。
2024最新激活全家桶教程，稳定运行到2099年，请移步至置顶文章：https://sigusoft.com/99576.html
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请联系我们举报，一经查实，本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处：https://sigusoft.com/24809.html
