面试算法数据结构-字符串 【Linux开发全栈程序员社区】 个人gitee:零声社区 全文约1.4w字,建议先收藏分次阅读,方便理解 1.0 本章导读 字符串相关的问题在各大互联网公司笔试面试中出现的频率极高,比如微软经典的单词翻转题:输入“I am a student.”,则输出“student. a am I”。 本章重点介绍6个经典的字符串问题,分别是旋转字符串、字符串包含、字符串转换成整数、回文判断、最长回文子串、字符串的全排列,这6个问题要么从暴力解法入手,然后逐步优化,要么多种思路多种解法。 读完本章后会发现,好的思路都是在充分考虑到问题本身的特征的前提下,或巧用合适的数据结构,或选择合适的算法降低时间复杂度(避免不必要的操作),或选用效率更高的算法。 1.1 旋转字符串 题目描述 给定一个字符串,要求把字符串前面的若干个字符移动到字符串的尾部,如把字符串“abcdef”前面的2个字符’a’和’b’移动到字符串的尾部,使得原字符串变成字符串“cdefab”。请写一个函数完成此功能,要求对长度为n的字符串操作的时间复杂度为 O(n),空间复杂度为 O(1)。 分析与解法 解法一:暴力移位法 初看此题,可能最先想到的方法是按照题目所要求的,把需要移动的字符一个一个地移动到字符串的尾部,如此我们可以实现一个函数,以完成移动一个字符到字符串尾部的功能,代码如下所示: 因此,若要把字符串开头的m个字符移动到字符串的尾部,则可以如下操作: 下面,我们来分析一下这种方法的时间复杂度和空间复杂度。 针对长度为n的字符串来说,假设需要移动m个字符到字符串的尾部,那么总共需要 mn 次操作,同时设立一个变量保存第一个字符,如此,时间复杂度为O(m n),空间复杂度为O(1),空间复杂度符合题目要求,但时间复杂度不符合,所以,我们得需要寻找其他更好的办法来降低时间复杂度。 解法二:三步反转法 对于这个问题,换一个角度思考一下。 将一个字符串分成X和Y两个部分,在每部分字符串上定义反转操作,如X^T,即把X的所有字符反转(如,X=”abc”,那么X^T=”cba”),那么就得到下面的结论:(X^TY^T)^T=YX,显然就解决了字符串的反转问题。 例如,字符串 abcdef ,若要让def翻转到abc的前头,只要按照下述3个步骤操作即可:首先将原字符串分为两个部分,即X:abc,Y:def;将X反转,X->X^T,即得:abc->cba;将Y反转,Y->Y^T,即得:def->fed。反转上述步骤得到的结果字符串X^TY^T,即反转字符串cbafed的两部分(cba和fed)给予反转,cbafed得到defabc,形式化表示为(X^TY^T)^T=YX,这就实现了整个反转。 如下图所示: 代码则可以这么写: 这就是把字符串分为两个部分,先各自反转再整体反转的方法,时间复杂度为O(n),空间复杂度为O(1),达到了题目的要求。 举一反三 1、链表翻转。给出一个链表和一个数k,比如,链表为1→2→3→4→5→6,k=2,则翻转后2→1→6→5→4→3,若k=3,翻转后3→2→1→6→5→4,若k=4,翻转后4→3→2→1→6→5,用程序实现。 2、编写程序,在原字符串中把字符串尾部的m个字符移动到字符串的头部,要求:长度为n的字符串操作时间复杂度为O(n),空间复杂度为O(1)。 例如,原字符串为”Ilovebaofeng”,m=7,输出结果为:”baofengIlove”。 3、单词翻转。输入一个英文句子,翻转句子中单词的顺序,但单词内字符的顺序不变,句子中单词以空格符隔开。为简单起见,标点符号和普通字母一样处理。例如,输入“I am a student.”,则输出“student. a am I”。 1.2 字符串包含 题目描述 给定两个分别由字母组成的字符串A和字符串B,字符串B的长度比字符串A短。请问,如何最快地判断字符串B中所有字母是否都在字符串A里? 为了简单起见,我们规定输入的字符串只包含大写英文字母,请实现函数bool StringContains(string &A, string &B) 比如,如果是下面两个字符串: String 1:ABCD String 2:BAD 答案是true,即String2里的字母在String1里也都有,或者说String2是String1的真子集。 如果是下面两个字符串: String 1:ABCD String 2:BCE 答案是false,因为字符串String2里的E字母不在字符串String1里。 同时,如果string1:ABCD,string 2:AA,同样返回true。 分析与解法 题目描述虽长,但题意很明了,就是给定一长一短的两个字符串A,B,假设A长B短,要求判断B是否包含在字符串A中。 初看似乎简单,但实现起来并不轻松,且如果面试官步步紧逼,一个一个否决你能想到的方法,要你给出更好、最好的方案时,恐怕就要伤不少脑筋了。 解法一 判断string2中的字符是否在string1中?最直观也是最简单的思路是,针对string2中每一个字符,逐个与string1中每个字符比较,看它是否在String1中。 代码可如下编写: 假设n是字符串String1的长度,m是字符串String2的长度,那么此算法,需要O(n*m)次操作。显然,时间开销太大,应该找到一种更好的办法。 解法二 如果允许排序的话,我们可以考虑下排序。比如可先对这两个字符串的字母进行排序,然后再同时对两个字串依次轮询。两个字串的排序需要(常规情况)O(m log m) + O(n log n)次操作,之后的线性扫描需要O(m+n)次操作。 关于排序方法,可采用最常用的快速排序,参考代码如下: 解法三 有没有比快速排序更好的方法呢? 我们换一种角度思考本问题: 假设有一个仅由字母组成字串,让每个字母与一个素数对应,从2开始,往后类推,A对应2,B对应3,C对应5,……。遍历第一个字串,把每个字母对应素数相乘。最终会得到一个整数。 利用上面字母和素数的对应关系,对应第二个字符串中的字母,然后轮询,用每个字母对应的素数除前面得到的整数。如果结果有余数,说明结果为false。如果整个过程中没有余数,则说明第二个字符串是第一个的子集了(判断是不是真子集,可以比较两个字符串对应的素数乘积,若相等则不是真子集)。 思路总结如下:按照从小到大的顺序,用26个素数分别与字符’A’到’Z’一一对应。遍历长字符串,求得每个字符对应素数的乘积。遍历短字符串,判断乘积能否被短字符串中的字符对应的素数整除。输出结果。 如前所述,算法的时间复杂度为O(m+n)的最好的情况为O(n)(遍历短的字符串的第一个数,与长字符串素数的乘积相除,即出现余数,便可退出程序,返回false),n为长字串的长度,空间复杂度为O(1)。 此种素数相乘的方法看似完美,但缺点是素数相乘的结果容易导致整数溢出。 解法四 如果面试官继续追问,还有没有更好的办法呢?计数排序?除了计数排序呢? 事实上,可以先把长字符串a中的所有字符都放入一个Hashtable里,然后轮询短字符串b,看短字符串b的每个字符是否都在Hashtable里,如果都存在,说明长字符串a包含短字符串b,否则,说明不包含。 再进一步,我们可以对字符串A,用位运算(26bit整数表示)计算出一个“签名”,再用B中的字符到A里面进行查找。 这个方法的实质是用一个整数代替了hashtable,空间复杂度为O(1),时间复杂度还是O(n + m)。 举一反三 1、变位词如果两个字符串的字符一样,但是顺序不一样,被认为是兄弟字符串,比如bad和adb即为兄弟字符串,现提供一个字符串,如何在字典中迅速找到它的兄弟字符串,请描述数据结构和查询过程。 1.3 字符串转换成整数 题目描述 输入一个由数字组成的字符串,把它转换成整数并输出。例如:输入字符串”123″,输出整数123。 给定函数原型,实现字符串转换成整数的功能,不能使用库函数atoi。 分析与解法 本题考查的实际上就是字符串转换成整数的问题,或者说是要你自行实现atoi函数。那如何实现把表示整数的字符串正确地转换成整数呢?以”123″作为例子:当我们扫描到字符串的第一个字符’1’时,由于我们知道这是第一位,所以得到数字1。当扫描到第二个数字’2’时,而之前我们知道前面有一个1,所以便在后面加上一个数字2,那前面的1相当于10,因此得到数字:1*10+2=12。继续扫描到字符’3’,’3’的前面已经有了12,由于前面的12相当于120,加上后面扫描到的3,最终得到的数是:12*10+3=123。 因此,此题的基本思路便是:从左至右扫描字符串,把之前得到的数字乘以10,再加上当前字符表示的数字。 思路有了,你可能不假思索,写下如下代码: 显然,上述代码忽略了以下细节:空指针输入:输入的是指针,在访问空指针时程序会崩溃,因此在使用指针之前需要先判断指针是否为空。正负符号:整数不仅包含数字,还有可能是以’+’或’-‘开头表示正负整数,因此如果第一个字符是’-‘号,则要把得到的整数转换成负整数。非法字符:输入的字符串中可能含有不是数字的字符。因此,每当碰到这些非法的字符,程序应停止转换。整型溢出:输入的数字是以字符串的形式输入,因此输入一个很长的字符串将可能导致溢出。 上述其它问题比较好处理,但溢出问题比较麻烦,所以咱们来重点看下溢出问题。 一般说来,当发生溢出时,取最大或最小的int值。即大于正整数能表示的范围时返回MAX_INT:;小于负整数能表示的范围时返回MIN_INT:-。 我们先设置一些变量:sign用来处理数字的正负,当为正时sign > 0,当为负时sign < 0n存放最终转换后的结果c表示当前数字 而后,你可能会编写如下代码段处理溢出问题: 但当上述代码转换” “会出错,因为正常的话理应得到MAX_INT:,但程序运行结果将会是:。 为什么呢?因为当给定字符串” “时,而MAX_INT是,即MAX_INT() < n10(\10),所以当扫描到最后一个字符‘9’的时候,执行上面的这行代码: 已无意义,因为此时(MAX_INT – n * 10)已经小于0,程序已经出错。 针对这种由于输入了一个很大的数字转换之后会超过能够表示的最大的整数而导致的溢出情况,我们有两种处理方式可以选择:一个取巧的方式是把转换后返回的值n定义成long long,即long long n;另外一种则是只比较n和MAX_INT / 10的大小,即:若n > MAX_INT / 10,那么说明最后一步转换时,n*10必定大于MAX_INT,所以在得知n > MAX_INT / 10时,当即返回MAX_INT。若n == MAX_INT / 10时,那么比较最后一个数字c跟MAX_INT % 10的大小,即如果n == MAX_INT / 10且c > MAX_INT % 10,则照样返回MAX_INT。 对于上面第一种方式,虽然我们把n定义了长整型,但最后返回时系统会自动转换成整型。咱们下面主要来看第二种处理方式。 对于上面第二种方式,先举两个例子说明下:如果我们要转换的字符串是””,那么当我扫描到字符’9’时,判断出 > MAX_INT / 10 = / 10 = (C语言里,整数相除自动取整,不留小数),则返回MAX_INT;如果我们要转换的字符串是””,那么判断最后一个字符’8’所代表的数字8与MAX_INT % 10 = 7的大小,前者大,依然返回MAX_INT。 一直以来,我们努力的目的归根结底是为了更好的处理溢出,但上述第二种处理方式考虑到直接计算n 10 + c 可能会大于MAX_INT导致溢出,那么便两边同时除以10,只比较n和MAX_INT / 10的大小,从而巧妙的规避了计算n\10这一乘法步骤,转换成计算除法MAX_INT/10代替,不能不说此法颇妙。 如此我们可以写出正确的处理溢出的代码: 从而,字符串转换成整数,完整的参考代码为: 举一反三 实现string到double的转换 分析:此题虽然类似于atoi函数,但毕竟double为64位,而且支持小数,因而边界条件更加严格,写代码时需要更加注意。 1.4 回文判断 题目描述 回文,英文palindrome,指一个顺着读和反过来读都一样的字符串,比如madam、我爱我,这样的短句在智力性、趣味性和艺术性上都颇有特色,中国历史上还有很多有趣的回文诗。 那么,我们的第一个问题就是:判断一个字串是否是回文? 分析与解法 回文判断是一类典型的问题,尤其是与字符串结合后呈现出多姿多彩,在实际中使用也比较广泛,而且也是面试题中的常客,所以本节就结合几个典型的例子来体味下回文之趣。 解法一 同时从字符串头尾开始向中间扫描字串,如果所有字符都一样,那么这个字串就是一个回文。采用这种方法的话,我们只需要维护头部和尾部两个扫描指针即可。 代码如下: 这是一个直白且效率不错的实现,时间复杂度:O(n),空间复杂度:O(1)。 解法二 上述解法一从两头向中间扫描,那么是否还有其它办法呢?我们可以先从中间开始、然后向两边扩展查看字符是否相等。参考代码如下: 时间复杂度:O(n),空间复杂度:O(1)。 虽然本解法二的时空复杂度和解法一是一样的,但很快我们会看到,在某些回文问题里面,这个方法有着自己的独到之处,可以方便的解决一类问题。 举一反三 1、判断一条单向链表是不是“回文” 分析:对于单链表结构,可以用两个指针从两端或者中间遍历并判断对应字符是否相等。但这里的关键就是如何朝两个方向遍历。由于单链表是单向的,所以要向两个方向遍历的话,可以采取经典的快慢指针的方法,即先位到链表的中间位置,再将链表的后半逆置,最后用两个指针同时从链表头部和中间开始同时遍历并比较即可。 2、判断一个栈是不是“回文” 分析:对于栈的话,只需要将字符串全部压入栈,然后依次将各字符出栈,这样得到的就是原字符串的逆置串,分别和原字符串各个字符比较,就可以判断了。 1.5 最长回文子串 题目描述 给定一个字符串,求它的最长回文子串的长度。 分析与解法 最容易想到的办法是枚举所有的子串,分别判断其是否为回文。这个思路初看起来是正确的,但却做了很多无用功,如果一个长的子串包含另一个短一些的子串,那么对子串的回文判断其实是不需要的。 解法一 那么如何高效的进行判断呢?我们想想,如果一段字符串是回文,那么以某个字符为中心的前缀和后缀都是相同的,例如以一段回文串“aba”为例,以b为中心,它的前缀和后缀都是相同的,都是a。 那么,我们是否可以可以枚举中心位置,然后再在该位置上用扩展法,记录并更新得到的最长的回文长度呢?答案是肯定的,参考代码如下: 代码稍微难懂一点的地方就是内层的两个 for 循环,它们分别对于以 i 为中心的,长度为奇数和偶数的两种情况,整个代码遍历中心位置 i 并以之扩展,找出最长的回文。 解法二、O(N)解法 在上文的解法一:枚举中心位置中,我们需要特别考虑字符串的长度是奇数还是偶数,所以导致我们在编写代码实现的时候要把奇数和偶数的情况分开编写,是否有一种方法,可以不用管长度是奇数还是偶数,而统一处理呢?比如是否能把所有的情况全部转换为奇数处理? 答案还是肯定的。这就是下面我们将要看到的Manacher算法,且这个算法求最长回文子串的时间复杂度是线性O(N)的。 首先通过在每个字符的两边都插入一个特殊的符号,将所有可能的奇数或偶数长度的回文子串都转换成了奇数长度。比如 abba 变成 #a#b#b#a#, aba变成 #a#b#a#。 此外,为了进一步减少编码的复杂度,可以在字符串的开始加入另一个特殊字符,这样就不用特殊处理越界问题,比如$#a#b#a#。 以字符串为例,插入#和$这两个特殊符号,变成了 S[] = “$#1#2#2#1#2#3#2#1#”,然后用一个数组 P[i] 来记录以字符S[i]为中心的最长回文子串向左或向右扩张的长度(包括S[i])。 比如S和P的对应关系:S # 1 # 2 # 2 # 1 # 2 # 3 # 2 # 1 #P 1 2 1 2 5 2 1 4 1 2 1 6 1 2 1 2 1 可以看出,P[i]-1正好是原字符串中最长回文串的总长度,为5。 接下来怎么计算P[i]呢?Manacher算法增加两个辅助变量id和mx,其中id表示最大回文子串中心的位置,mx则为id+P[id],也就是最大回文子串的边界。得到一个很重要的结论:如果mx > i,那么P[i] >= Min(P[2 * id – i], mx – i) C代码如下: 下面,令j = 2*id – i,也就是说j是i关于id的对称点。 当 mx – i > P[j] 的时候,以S[j]为中心的回文子串包含在以S[id]为中心的回文子串中,由于i和j对称,以S[i]为中心的回文子串必然包含在以S[id]为中心的回文子串中,所以必有P[i] = P[j]; 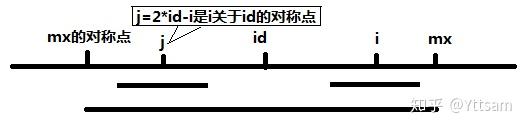

2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/21585.html