运算放大器作为微分器电路、公式及原理 运算放大器微分器或微分放大器是与积分器电路相反的电路配置。它产生一个输出信号，其中瞬时幅度与施加的输入电压的变化率成正比。 从数学上讲，微分器的输出信号是输入信号的一阶导数。例如，如果输入信号是斜坡信号，则以运算放大器作为微分器的电路的输出将是简单的 DC（因为斜坡信号的变化率是恒定的）。类似地，如果输入信号是正弦波，则输出信号也是正弦波，但相位差为 90°。 仅具有 RC 网络的微分器称为无源微分器，而具有晶体管和运算放大器等有源电路组件的微分器称为有源微分器。与简单的 RC 微分器相比，有源微分器具有更高的输出电压和更低的输出电阻。 运算放大器微分器是一个反相放大器，它使用一个与输入电压串联的电容器。微分电路通常设计为响应三角形和矩形输入波形。 微分器在正弦波输入上运行时具有频率限制；该电路会衰减所有低频信号分量，并在输出端仅允许高频分量。换句话说，电路就像一个高通滤波器。 理想运算放大器微分电路 运算放大器差分放大器使用与输入电压源串联的电容器，如下图所示。
对于直流输入，输入电容C 1达到其电位后，不能接受任何电荷，表现为开路。运算放大器的同相输入端通过提供输入偏置补偿的电阻器 R comp接地，反相输入端通过反馈电阻器 R f连接到输出端。 因此，电路的行为类似于电压跟随器。 当输入为正向电压时，电流I流入电容C 1，如图所示。由于流入运算放大器内部电路的电流为零，因此实际上所有电流 I 都流过电阻器 R f。输出电压为， V out = – (I * R f ) 这里，该输出电压与输入电压的变化率成正比。 从图中可以看出，节点“X”实际上是接地的，节点“Y”也处于接地电位，即 V X = V Y = 0 。 从输入端，电流 I 可以表示为： I = C 1 {d(V in – V X ) / dt} = C 1 {d(V in ) / dt} 从输出端，电流 I 为： I = -{(V out – V X ) / R f } = -{V out / R f } 将上述两个电流方程相等，得到： C 1 {d(V in ) / dt} = -V out / R f V out = -C 1 R f {d(V in ) / dt} 上式表明输出是 C 1 R f乘以输入电压的微分。乘积 C 1 R f称为微分电路的 RC 时间常数。负号表示输出相对于输入异相 180° 。 这种有源微分放大器电路的主要优点是微分所需的时间常数小。 输入和输出波形 现在让我们看看不同输入信号的输出波形。当幅度为 V m的阶跃输入（DC 电平）应用于运算放大器微分器时，输出在数学上可以表示为， V out = – C 1 R f {d(V m ) / dt} 为简单起见，假设积 C 1 R f 是实数。 因此， V out = 0 ，因为幅度 V m是恒定的并且 d(V m ) / dt = 0。 但实际上，输出不为零，因为输入阶跃波需要有限的时间才能从 0 伏上升到 V m伏。因此，输出在时间 t = 0 时看起来像一个尖峰，如下图所示。
如果将微分器的输入变为方波，则输出将是由正负尖峰组成的波形，对应于电容器的充电和放电，如下图所示。 
对于正弦波输入，在数学上表示为 V (t) = V m sin ωt，其中 V m是输入信号的幅度，t 是周期，微分器的输出为： V out = – C 1 R f {d(V m sin ωt) / dt} 为简单起见，假设乘积 C 1 R f是实数。 V out = – V m ω ωt 因此，对于正弦波输入，微分器的输出是余弦波，输入输出波形如下图所示。 
理想微分器的频率响应 运算放大器微分器的增益直接取决于输入信号的频率。因此，对于 f = 0 的 DC 输入，输出也为零。随着输入信号频率的增加，输出也会增加。理想微分器的频率响应如下图所示。
频率f 1是微分器的增益变为1的频率。从图中可以看出，对于小于f 1的频率，增益小于1。对于 f 1，增益变为单位 (0 dB)，超过 f 1，增益以每十倍频增加 20dB。 实用运算放大器微分电路 对于理想的微分器，增益随着频率的增加而增加。因此，在某些较高频率下，微分器可能会变得不稳定并引起振荡，从而产生噪声。 在实际的微分电路中可以避免或纠正这些问题，该电路使用与输入电容串联的电阻R 1和与反馈电阻并联的电容C f，如下图所示。
实际运算放大器差分放大电路的输出电压为： V out = – C 1 R f {d(V in ) / dt} 即，输出电压是C 1 R f乘以输入电压的微分。 电阻R 1和电容C f的加入使电路稳定在较高频率，同时也降低了噪声对电路的影响。 实用微分器的频率响应 实际微分器的增益随着频率的增加而增加，并且在特定频率 f 1处，增益变为单位 (0 dB)。增益继续以每十倍频 20dB 的速率增加，直到输入频率达到频率 f 2。 超出输入信号的这个频率，微分器的增益开始以每十倍频 20dB 的速率下降。这种效果是由于增加了电阻器 R 1和电容器 C f。实际微分器的频响曲线如下图所示。 
运算放大器微分器的应用 微分放大器最常设计用于处理三角形和矩形信号。微分器还可用作波形整形电路，以检测输入信号中的高频分量。 运算放大器作为微分器的总结 运算放大器微分放大器是一种反相放大器电路配置，它使用电抗件（通常是电容器而不是电感器）。微分器对输入信号对时间进行数学微分运算，即瞬时输出电压与输入信号的变化率成正比。微分电路通常用于对三角形和矩形信号进行操作。在正弦波输入上运行时，微分电路具有频率限制。
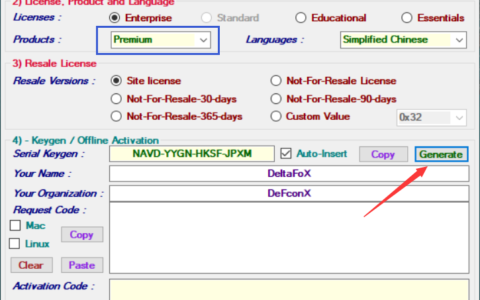
2024最新激活全家桶教程，稳定运行到2099年，请移步至置顶文章：https://sigusoft.com/99576.html
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请联系我们举报，一经查实，本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处：https://sigusoft.com/21413.html
