1. 激活谷首页
  2. 激活谷笔记

积分运算电路怎么计算_比例积分电路

• 激活谷笔记

积分运算电路怎么计算_比例积分电路电子技术——滤波器：微分积分电路一、PID运放PID控制系统由比例控制(proportion)，积分控制(integral)，微分控制(differential)三个分量对输入输出之间关系进行控制。能够实现输出的稳定性控制。（1.1

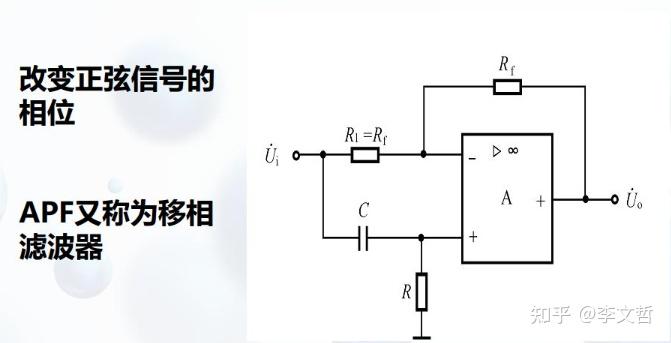
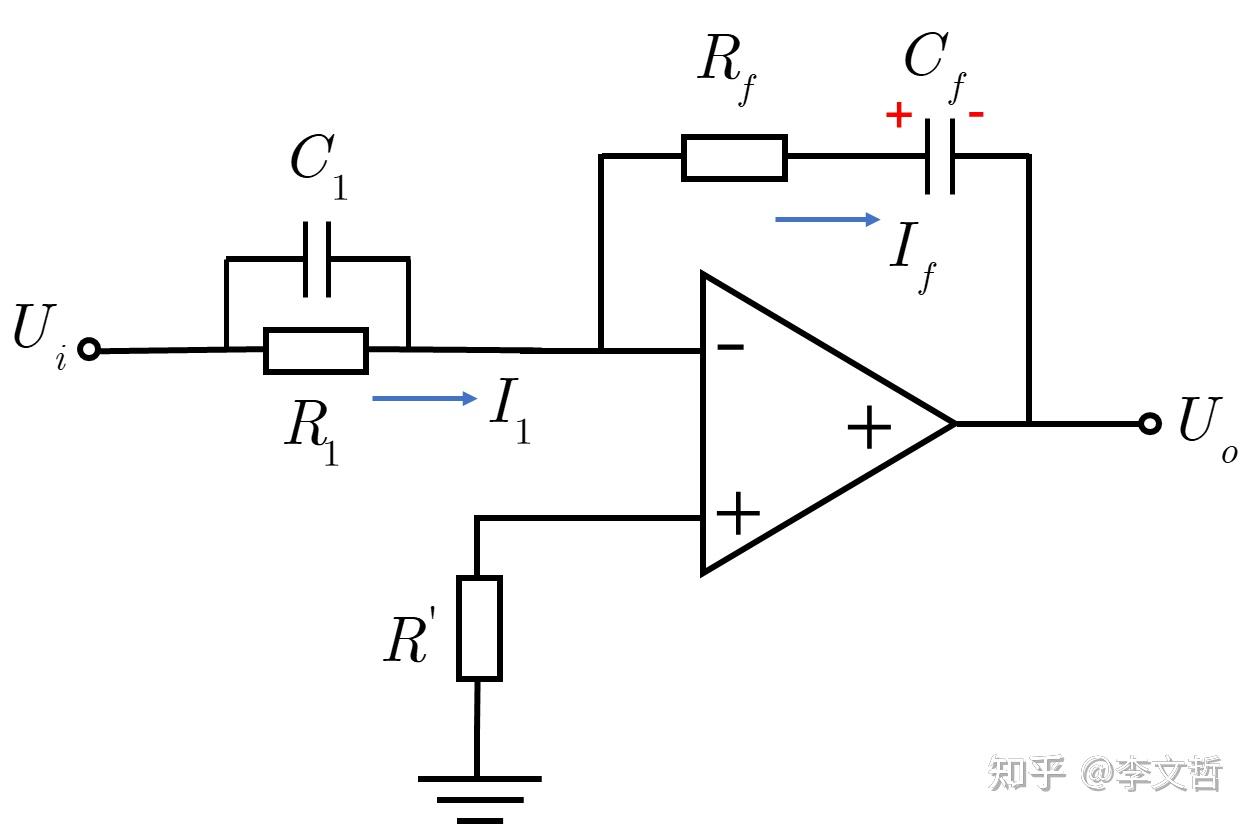
电子技术——滤波器：微分积分电路 　　一、PID运放 　　PID控制系统由比例控制(proportion)，积分控制(integral)，微分控制(differential)三个分量对输入输出之间关系进行控制。能够实现输出的稳定性控制。 　　（1.1）积分运算 　　电容位于反馈端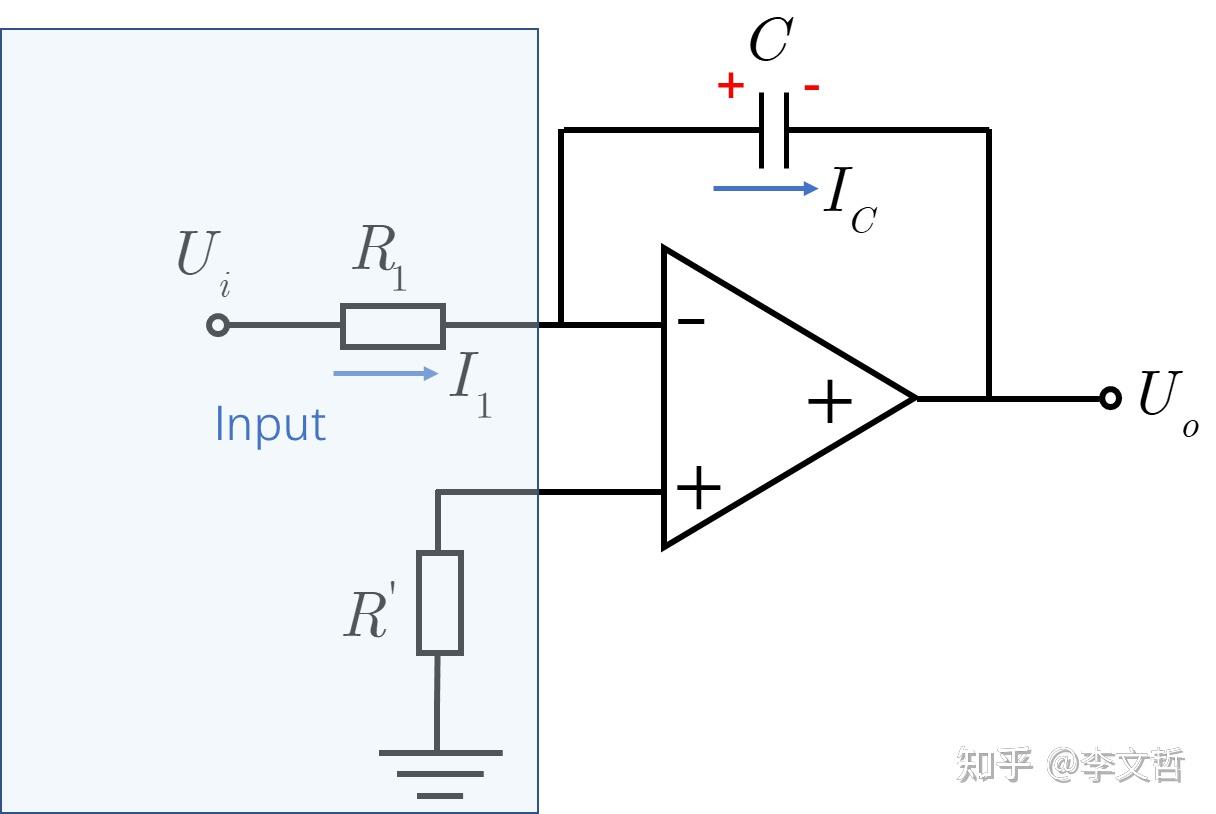
积分运算电路怎么计算_比例积分电路
积分运算电路怎么计算_比例积分电路 　　
虚短： U_+= U_-=0V\\ 续断：I_i =\frac{U_i}{R_i}=I_c=C\frac{dU_C}{dt}\\ U_0 = -U_C = -\frac{1}{RC}[\int _{t_1}^{t_2}U_idt+U(t_1)]\\反相加法积分，即在输入端并联若干电源
U_x ，有对应源内阻
R_{ix} ，输电流变为
I_i = \sum I_x = \sum\frac{U_x}{R_x} 　　（1.2）微分运算 　　电容位于输入端
积分运算电路怎么计算_比例积分电路
积分运算电路怎么计算_比例积分电路 　　
虚短： U_+= U_-=0V\\ 续断：I_c =I_i=C\frac{dU_c}{dt}\\ U_0 =-I_fR_f=-CR_f\frac{dU_c}{dt}=-CR_f\frac{dU_i}{dt}\\ 　　（1.3）PID运放 　　
积分运算电路怎么计算_比例积分电路
积分运算电路怎么计算_比例积分电路 　　
虚短： U_+= U_-=0V\\ 续断：I_i =I_f=C_f\frac{dU_c}{dt}\\ I_i=\frac{U_i}{R_1}+C_1\frac{dU_i}{dt}\\ \begin{align} U_0 =& -U_C-I_fR_f \\ =& -\frac{1}{C_fR_1}\int U_i dt-\frac{C_1}{C_f}\int dU_i\\ & -\frac{R_f}{R_i}U_i-R_fC_1\frac{dU_i}{dt}\\ \end{align}\\ 　　简化成对应的PID三个分量的，则为 　　
U_o=-(\frac{R_f}{R_1}+\frac{C_1}{C_f})U_i+ R_fC_1\frac{dU_i}{dt}+\frac{1}{R_1C_f}\int U_idt\\ 　　当
R_f=0,C_1\neq0 时，PID控制电路退化为PI控制电路
U_o=-(\frac{R_f}{R_1}+\frac{C_1}{C_f})U_i+\frac{1}{R_1C_f}\int U_idt\\PI控制电路能够控制积累误差，抑制输入端的噪声与干扰。 　　当
C_f=0 （电容短路）时，电路退化为PD控制电路 　　
U_o=-(\frac{R_f}{R_1}+\frac{C_1}{C_f})U_i+ R_fC_1\frac{dU_i}{dt}\\PD控制电路能够起到加速作用 　　二、滤波器性能参数 　　滤波器 　　使指定频率的信号通过，其余频率的信号被阻断或衰减。通带电压放大倍数
A_{up} 　　LPF（低通滤波器）
A_{up}=\left| \dot A_u \right|_{f=0} 　　HPF（高通滤波器）
A_{up}=\left| \dot A_u \right|_{f=\infty} 电压传递函数 　　
A_u(S)=\frac{U_o(s)}{U_i(s)} 通带截止频率
f_p 　　
\left| \dot A_u \right|_{f_p}=0.707A_{up} 　　三、电路的拉式变换分析 　　在分析交变电路的过程中，通常涉及到高阶微分方程的求解，正常求解十分复杂。因此采用拉普拉斯变换，将电路由时域
t 变化到复数域
s 上。将微分方程的求解变化为加减乘除的线性方程。 　　具体而言，
Laplace 变换的过程如下对求解函数进行
Laplace变换：\mathscr L(f(t))=F(s)=\int_0^{+\infty}f(t)e^{-st}dt 得到像函数
F(S) 对求解函数的导函数进行
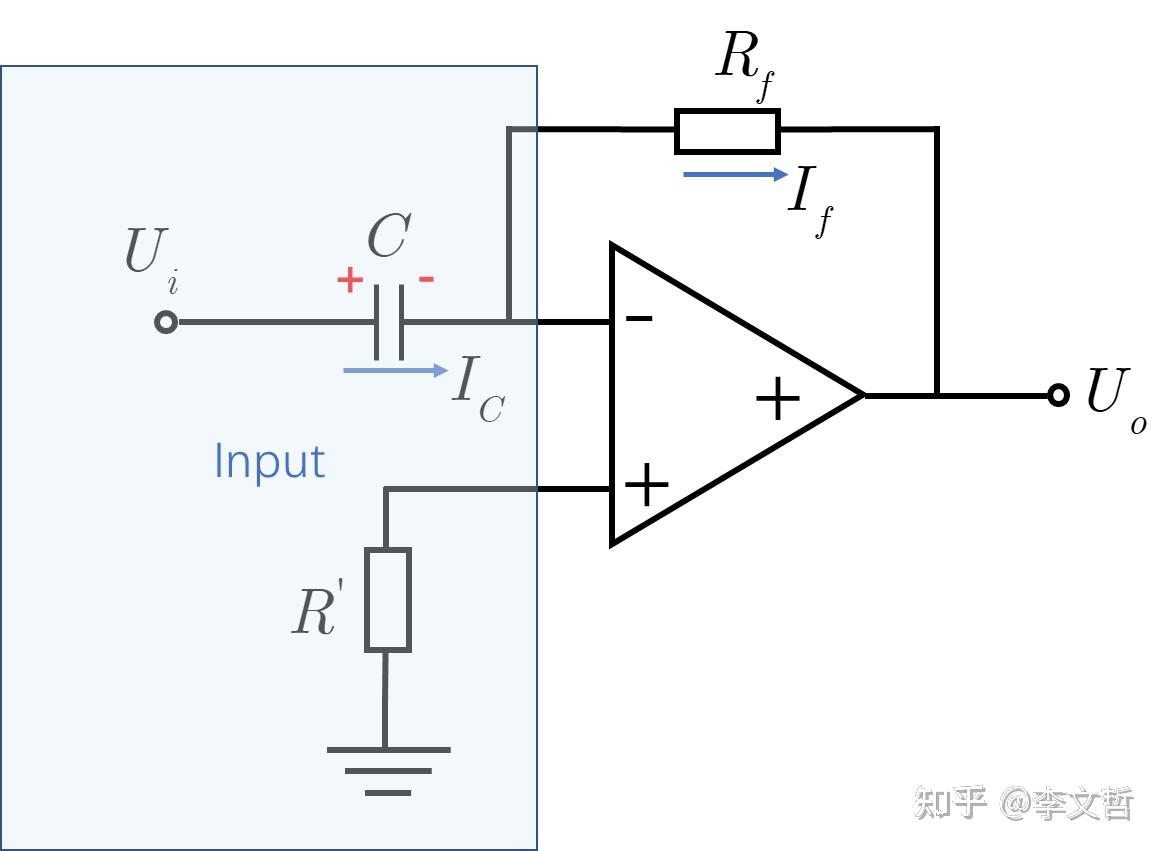
Laplace变换： \begin{align} \mathscr{L}[f^{(n)}(t)]=s^nF(s)-\sum_{i=0}^{n-1}s^{n-1-i}f^{(i)}(0) \end{align} 对求解函数的积分函数进行
Laplace变换：\mathscr L[(\int_0^t)^n f(t) (dt)^n]=\frac{1}{s^n}\mathscr L[f(t)] 将原微分方程化为线性方程，进行求解得到像函数
F(s) 像函数进行
Laplace反变换：f(t)=\mathscr L^{-1}[F(s)]-\frac{1}{2\pi}\int_{\beta-j\infty}^{\beta+j\infty}F(s)e^{st}ds 　　电阻 　　变换前：
u(t)=Ri(t) 变换后：
U(s)=RI(s) 　　电容 　　变换前： 　　
u_C(t)=\frac{1}{C}\int_0^{t}i_C(\tau)d\tau+u_C(0) 变换后： 　　
\begin{align} U_C(s)&=\frac{1}{sC}I_C(s)+u_C(0)\int_0^{+\infty}e^{st}dt\\ &=\frac{1}{sC}I_C(s)+\frac{u_C(0)}{s} \end{align} 　　电感 　　变换前： 　　
u_L(t)=L\frac{di_L}{dt} 变换后： 　　
U_L(s)=L(sI_L(s)-i_L(0)) 　　四、无源滤波器 　　（4.1）无源低通滤波器LPF 　　空载时，电路形式如图
积分运算电路怎么计算_比例积分电路
积分运算电路怎么计算_比例积分电路 　　输出的电压放大倍数可以计算为（拉普拉斯变换后）： 　　
A_u(s)=\frac{U_o(s)}{U_i(s)}=\frac{U_C(s)}{U_C(s)+U_R(s)}=\frac{\frac{1}{sC}I_C(s)}{(R+\frac{1}{sC})I_C(s)}=\frac{1}{1+sCR} 　　在忽略拉普拉斯变换的衰减项
\sigma 后，带入
s=j\omega 　　
\dot A_u=\frac{\dot U_o}{\dot U_i}=\frac{1}{1+j\omega RC}=\frac{1}{1+j\frac{\omega}{\omega_0}}=\frac{1}{1+j\frac{f}{f_0}}\\ 其中
\omega_0=\frac{1}{RC}称为RC电路的固有角频率，
f_0=\frac{1}{2\pi RC} 称为电路的固有频率。 　　低通滤波器，输入信号的频率为0，通带电压放大倍数
A_{up}=1 。 　　通带截止频率
\left|\dot A_{f_p} \right|=\frac{1}{\sqrt{2}}A_{up} ,则有
\left| \frac{1}{1+j\frac{f_p}{f_0}} \right|=\frac{1}{\sqrt 2}\Rightarrow f_p=f_0=\frac{1}{2\pi RC}
积分运算电路怎么计算_比例积分电路
积分运算电路怎么计算_比例积分电路通带截止频率以后，工程近似线性， 　　带载时，电路形式如图
积分运算电路怎么计算_比例积分电路
积分运算电路怎么计算_比例积分电路 　　低通滤波器，输入信号的频率为0，通带电压放大倍数
A_{up}=\frac{R_L}{R+R_L} 。 　　输出的电压放大倍数可以计算为（拉普拉斯变换后）： 　　
A_u(s)=\frac{U_o(S)}{U_i(S)}=\frac{U_C(s)}{U_C(s)+(\frac{U_C(s)}{R_L}+I_C(s))R}= \frac{\frac{1}{sC}I_C(s)}{(\frac{1}{sC}+\frac{R}{sCR_L}+R)I_C(s)}=\frac{\frac{R}{R+R_L}}{1+\frac{RR_L}{R+R_L}sC} 　　在忽略拉普拉斯变换的衰减项
\sigma 后，带入
s=j\omega 　　
\dot A_u(s)==\frac{\dot A_{up}}{1+\frac{RR_L}{R+R_L}j\omega C}=\frac{\dot A_{up}}{1+j\frac{f}{f_p}} 　　此时的通带截止频率
f_p=\frac{1}{2\pi\frac{RR_L}{R+R_L}C}
积分运算电路怎么计算_比例积分电路
积分运算电路怎么计算_比例积分电路 　　（4.2）无源高通滤波器HPF 　　此处仅分析空载时的载流情况，分析与低通类似。
积分运算电路怎么计算_比例积分电路
积分运算电路怎么计算_比例积分电路 　　（4.3）滤波器对偶特性 　　低通滤波器与高通滤波器可以发现呈现对偶性质
积分运算电路怎么计算_比例积分电路
积分运算电路怎么计算_比例积分电路左侧为低通滤波器，右侧为高通滤波器，下述为其幅频图
积分运算电路怎么计算_比例积分电路
积分运算电路怎么计算_比例积分电路 　　简单而言，只要掌握了低通滤波器的电路设计方法，将电路中的滤波部分的电容电阻呼唤位置即可实现低通——高通互换。因此统一仅介绍低通滤波器，高通滤波器自然对偶即可。 　　五、有源滤波器 　　无源滤波器的最大电压放大倍率仅为1，且负载能力弱，截止频率甚至与负载电阻相关，不是固定参数。为了改进，实现电压放大功能，我们将滤波器与运算放大器相连，实现有源滤波电路。 　　在设计有源滤波电路的过程中，通常将滤波器与运放输入端相连。且每串联一个滤波器，在解算电路参量时，微分方程的阶数就高一阶，解算也更复杂。 　　（5.1）一阶同相输入滤波放大器 　　一阶LPF的电路图如下，滤波器连接在运放的同相输入端，起到同向放大的作用，此时，在分析滤波器时，由于虚短虚断，同相输入端可以视作无连接，为无负载状态。 　　分析滤波器时，应当先分析通带电压放大倍数，再列出电压传递函数，并推导截止频率。
积分运算电路怎么计算_比例积分电路
积分运算电路怎么计算_比例积分电路 　　由于频率为0，输入为常电压，滤波器端因此无电流通过。通带电压放大倍数
A_{up}=(1+\frac{R_f}{R_1})\frac{U_+}{U_i}=1+\frac{R_f}{R} 　　电压传递函数(幅频特性)
A_u(s)=\frac{U_0(s)}{U_i(s)}=\frac{1}{1+sCR}A_{up}=\frac{1}{1+j\frac{f}{f_0}}A_{up} 　　由于滤波看作无负载状态，即通带截止频率
f_p=f_0=\frac{1}{2\pi RC}
积分运算电路怎么计算_比例积分电路
积分运算电路怎么计算_比例积分电路幅频特性曲线图，横坐标为10倍间隔 　　（5.2）二阶同相输入放大滤波器 　　二阶有源低通滤波电路图如下，与一阶讨论相类似，不再过多注释说明。
积分运算电路怎么计算_比例积分电路
积分运算电路怎么计算_比例积分电路此时幅频特性输出为40dB/十频程通带电压放大倍数
A_{up}=1+\frac{R_f}{R} 电压传递函数
A_u(s)=\frac{A_{up}}{1+3sCR+(sCR)^2} ,推导如上图。通带截止频率
1+3j\frac{f_p}{f_0}-(\frac{f_p}{f_0})^2=\sqrt2 　　显然可知固有频率
f_0=\frac{1}{2\pi RC} 并不等于通带截止频率
f_p 　　（5.3）一阶反相输入运算放大器 　　不过多讨论，一切如图。
积分运算电路怎么计算_比例积分电路
积分运算电路怎么计算_比例积分电路 　　六、带通带阻滤波器 　　由高通滤波器和低通滤波器，对运放输入端进行设计，实现对特定频段的信号进行筛选，使之通过或阻断。 　　（6.1）带通滤波器 　　低通滤波器和高通滤波器串联，其实现逻辑如下。
积分运算电路怎么计算_比例积分电路
积分运算电路怎么计算_比例积分电路 　　要求低通滤波器的通带截止频率
f_{p1} 大于高通滤波器的通带截止频率
f_{p2}。实现后的滤波效果如下
积分运算电路怎么计算_比例积分电路
积分运算电路怎么计算_比例积分电路 　　具体的电路设计如下，这是一个压控电压源的带通滤波电路。正反馈节点连接的两端即分别为低通滤波器和高通滤波器。
积分运算电路怎么计算_比例积分电路
积分运算电路怎么计算_比例积分电路 　　（6.2）带阻滤波器 　　低通滤波器和高通滤波器并联，其实现逻辑如下。
积分运算电路怎么计算_比例积分电路
积分运算电路怎么计算_比例积分电路 　　且要求高通滤波器的通带截止频率
f_{p1} 大于低通滤波器的通带截止频率
f_{p2}实现后的滤波效果如下
积分运算电路怎么计算_比例积分电路
积分运算电路怎么计算_比例积分电路 　　具体的电路设计如下，这是一个压控电压源的带通滤波电路。正反馈节点连接的两端即分别为低通滤波器和高通滤波器。
积分运算电路怎么计算_比例积分电路
积分运算电路怎么计算_比例积分电路 　　（6.2）全通滤波器APF 　　用于改变相位。
积分运算电路怎么计算_比例积分电路
积分运算电路怎么计算_比例积分电路

2024最新激活全家桶教程，稳定运行到2099年，请移步至置顶文章：https://sigusoft.com/99576.html

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请联系我们举报，一经查实，本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处：https://sigusoft.com/21248.html

赞 (0)
0
上一篇 2024年 9月 15日
下一篇 2024年 9月 15日

相关推荐

关注微信