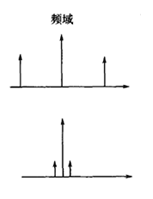
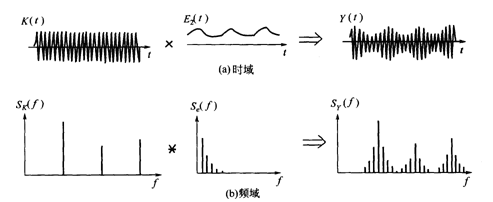
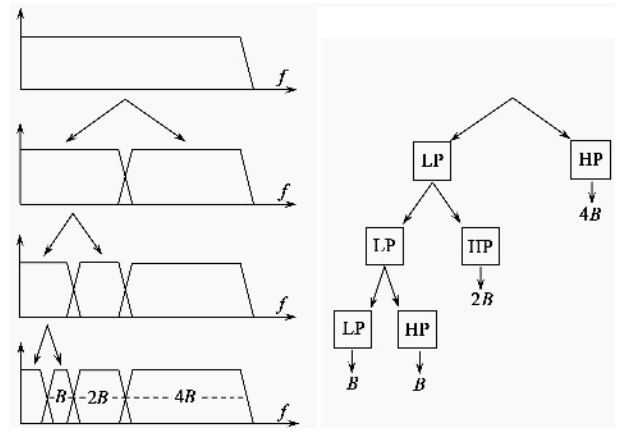
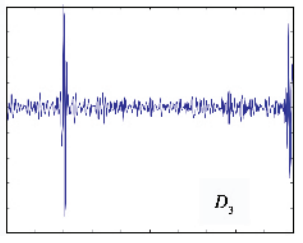
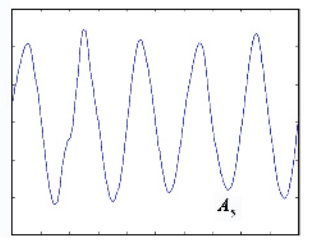
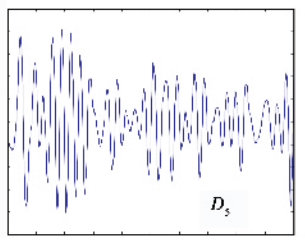
信号频域分析方法的理解(频谱、能量谱、功率谱、倒频谱、小波分析) 信号的频域分析方法多种多样,这里针对较为常见的(频谱、能量谱、功率谱、倒频谱、小波分析)集中进行说明。这些方法的MATLAB代码实现参见文章频域特征值提取的MATLAB代码实现(频谱、功率谱、倒频谱) 在看这篇文章之前可以参看之前的两篇,其中涉及一些时域特征值介绍和能量、功率信号区别的介绍: Mr.括号:信号的各种时域分析方法的理解 Mr.括号:能量信号和功率信号的分别 文章如要转载请私信与我联系,并注明来源知乎专栏与信号处理有关的那些东东作者Mr.括号。 一、频谱 一般来说,频谱分析指的是将信号做傅里叶变换从而进行分析。频谱分析是包括幅频谱和相频谱两张图的。不过最常用的是幅频谱。 频谱分析是最常用和最重要也是最基础的频域分析方法。在这里不详细展开说了,不了解概念的可以参考这篇文章: Heinrich:如果看了这篇文章你还不懂傅里叶变换,那就过来掐死我吧 时常会见到几个概念:DFT,DTFT,DFS,FFT,FT, FS等等。这些概念怎么区分?看这篇文章就能搞懂:一幅图弄清DFT与DTFT,DFS的关系 – BitArt – 博客园 在这里概括一下(不感兴趣的话可以直接跳过): FT(Fourier Transformation):傅里叶变换。就是我们理论上学的概念,但是对于连续的信号无法在计算机上使用。其时域信号和频域信号都是连续的。 DTFT(Discrete-time Fourier Transform):离散时间傅里叶变换。这里的“离散时间”指的是时域上式离散的,也就是计算机进行了采样。不过傅里叶变换后的结果依然是连续的。 DFT(Discrete Fourier Transform):离散傅里叶变换。在DTFT之后,将傅里叶变换的结果也进行离散化,就是DFT。 也就是说:FT时域连续、频域连续;DTFT时域离散、频域连续;DFT时域离散、频域离散。 FFT(Fast Fourier Transformation):快速傅里叶变换。就是DFT的快速算法,一般工程应用时用的都是这种算法。 FS(Fourier Series):傅里叶级数。是针对时域连续周期信号提出的,结果是离散的频域结果。 DFS(Discrete Fourier Series):离散傅里叶级数。是针对时域离散周期信号提出的,DFS与DFT的本质是一样的。 另外补充几点相关知识:在实际计算中通常使用快速傅里叶变换(FFT)。它是一种用来计算DFT(离散傅里叶变换)和IDFT(离散傅里叶反变换)的一种快速算法。随机信号是无法做傅里叶变换的(*这里要再补充) 二、能量谱 要理解能量谱和功率谱,首先要弄明白能量有限信号和功率有限信号(参看之前的文章能量信号和功率信号的分别)。 能量谱也叫能量谱密度,能量谱密度描述了信号或时间序列的能量如何随频率分布。能量谱是原信号傅立叶变换的平方。 三、功率谱 功率谱是功率谱密度函数(PSD)的简称,它定义为单位频带内的信号功率。 功率谱是针对功率信号来说的。功率谱的推导公式相对复杂,不过幸运的是维纳-辛钦定理证明了:一段信号的功率谱等于这段信号自相关函数的傅里叶变换。 所以求功率谱就有了两种方法:1.(傅立叶变换的平方)/(区间长度);2.自相关函数的傅里叶变换。这两种方法分别叫做直接法和相关函数法。 功率谱这里存在着一些问题,整理如下: 1.功率谱密度的单位是什么,看有的写的是dB,还有的说是W/Hz。 功率谱的单位是W/Hz,单位是dB时是做了对数处理(10logX)。取对数的目的是使那些振幅较低的成分相对高振幅成分得以拉高,以便观察掩盖在低幅噪声中的周期信号。 2.求功率谱的两种方法有什么区别么? 从原理上讲似乎没什么区别,从MATLAB仿真结果上来看,相关函数法对噪声的抑制效果更好,图线更平滑。(见频域特征值提取的MATLAB代码实现(频谱、功率谱、倒频谱)) 3.FFT和PSD都是表示的频谱特性,帮助我们找出峰值的位置,那么有了FFT为什么还要提出PSD? 信号分为确定信号和随机信号,而确定信号又分为能量信号和功率信号,随机信号一定是功率信号。根据狄里赫利条件,能量信号可以直接进行傅里叶变换,而功率信号不行。对于无法做傅里叶变换的信号,只能走一步弯路,先求自相关,再做傅里叶。但是物理意义上就是功率谱了。不过总之得到了信号的频率特性。 4.既然为什么随机信号的一次FFT没有意义却还能(傅立叶变换的平方)/(区间长度)得到功率谱? 对随机信号直接做FFT的做法其实就是截断成能量信号进行处理,这种处理不符合随机信号定义,但之所以这样做,是做短时频域分析下作的近似处理。(这里希望能有大神能给出更好的解释)所以总结,频谱和能量谱(也叫能量谱密度)是傅里叶变换得到的复数结果和模平方的关系;而功率谱(也就是功率谱密度)是针对随机信号分析提出的概念。 更多讨论可以参看:随机信号傅里叶变换和功率谱密度图给出的信息有什么不同 – MATLAB中文论坛 四、倒频谱 倒频谱(Cepstrum)也叫倒谱、二次谱和对数功率谱等。倒频谱的工程型定义是:信号功率谱对数值进行傅立叶逆变换的结果。(信号→求功率谱→求对数→求傅里叶逆变换) 为什么翻译作倒频谱呢?我个人的理解是,频谱(功率谱)反应的频率特征点横坐标是频率f(Hz),在倒频谱中对应的特征点的横坐标是时间t(s),而f与t互为倒数。从这里也可以看出,虽然倒频谱也叫“频谱”,其横坐标却并不是频率,而是时间。 那么倒频谱有什么好处呢?“该分析方法方便提取、分析原频谱图上肉眼难以识别的周期性信号,能将原来频谱图上成族的边频带谱线简化为单根谱线,受传感器的测点位置及传输途径的影响小。” 这都是啥意思?一条条解释: 1.方便提取、分析原频谱图上肉眼难以识别的周期性信号 我们知道,频谱分析就是为了提取原始信号中的周期性信号的,怎么频谱中的信号还会有周期性?这就又涉及到两个概念:调制和边频带。 调制分为幅值调制和频率调制。下面以齿轮的幅值调制为例进行说明:齿轮的振动信号主要包括两部分,分别是齿轮啮合振动信号(高频)和齿轮轴的转频振动信号(低频),时域和频域曲线分别如下图所示: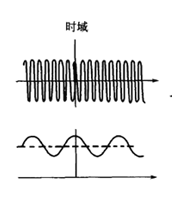


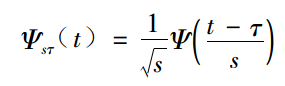
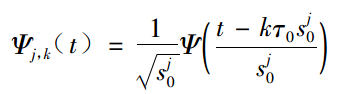

2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/21007.html