ZoomFFT算法能提高频率分辨率吗？ 请教诸位，zoomfft算法能提高频率分辨率吗？从原理上看貌似没有提高啊，重采样过程中采样频率降低，采样点减少，采样时间不变，分辨率应该没有提高啊。而很多说法把zoomfft当做提高分辨率的方法，有的说法说其只能减少计算量 谢邀 这个算法我还是第一次听说，算法的主要目的是细分频谱，也就是你所说的提高频率分辨率。具体源代码我有看到，不过工作机不方便上网，pad上没有Matlab，等我回宿舍运行程序看看吧！ —————————————————————————————————————————– Update 2014年4月30日 20:31:31 ZoomFFT算法的确可以细分频谱，因为我们在做FFT变换时，其实是损失（或者说，是没有表现出来）了一些信息的，而ZoomFFT可以把这些信息找回来。 假设信号采样率是Fs，采样点数是N，则传统FFT的频率分辨率dF=Fs/N，要使分辨率高，则dF越小越好。但是信号采样率Fs不能太低，信号采样时间也不可能太长（硬件限制、或者信号本身就不长），这时候就需要采用其它其它方法了。当然其它方法肯定是需要付出代价的，ZoomFFT的策略是以减小频率带宽为代价，提高频率分辨率。这个策略有时是很有效的，因为有时候我们只对某个带宽内的信号感兴趣。 这就像我们用摄像机拍摄远处的景物，取景范围大的时候，对于局部的分辨率定然是有限的，要是想仔细察看细节，就只能拉近镜头，看到局部放大。 放一张图吧，可以很直观的看到频域插值的效果：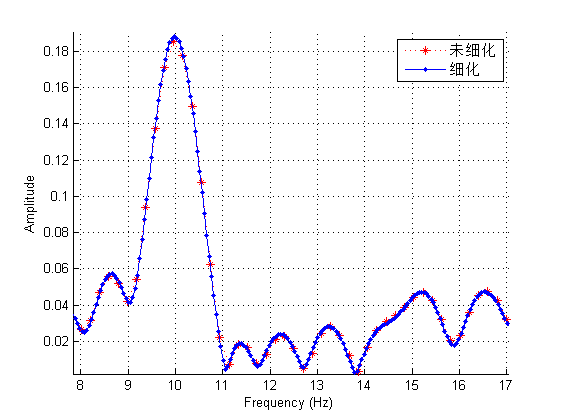
—————————————————————————————————————————– 以下是个人的一些猜想，不做证明，愿意与大家探讨 1. 这个频域插值的插值方式是sinc插值。 2. 之所以提高频率分辨率需要增加信号时间长度，就是因为两个频率分量的信号，如果频率差很小，那么需要较长的时间才能体现出相位的差别。而ZoomFFT算法则采用了另一种方法：不延长时间，而是增大频率差。怎么增大？调制移频。具体细节我还没有想明白，大家可以一起讨论下~ zoomFFT这种频率细化的方法主要步骤是：移频-抗混叠滤波-重采样-复FFT处理-频率调整，这种方法是利用降低采样频率Fs（但又不会产生频率混叠），而采样点数N不变的，来提高所关心频段的频率分辨率（单纯的FFT在降低Fs时受采样定理限制，不能太小，不然会产生混叠）。 其实这种方法方法，在降低采样频率，保持采样点数不变的情况下，必然还是会导致采样时间的增加，这是我们不希望看到的。 所以个人感觉这种方法在采样时间固定（不是采样点数N不变）的情况下，是不能提高频率分辨率的。 而减少计算量是对的，zoomFFT可以选择感兴趣的频段对其进行频谱分析（要经过滤波处理），相对来说所需的采样频率Fs1就比较低，而全频段的FFT分析，为了防止频率混叠，需要满足Fs2>2*Fc （Fc为信号中最大频率），可见Fs1<Fs2。而频谱分辨率为Fs/N = Fs/(Fs*t)=1/t 只与采样时间有关（t为采样时间），这时要使这两种算法频率分辨率相同，只需要使其采样时间相同，由于Fs1<Fs2，则ZoomFFT的采样点数N1<全频段FFT的采样点数N2，从而zoomFFT的计算量是N1*log2(N1)，FFT的计算量是N2*log2(N2)，相对来说计算量减小了。 还有一点值得注意，zoomFFT在进行复FFT处理前要进行抗混叠滤波，这也有一定的计算量。 很多时候，分析振动噪声时，可能要求集中一个有限的频率区间fmin≤f≤fmax，需要对这个频率区间作细化处理，也就是所谓的zoomFFT。该方法本质上是基于频移傅立叶变换对。这个傅立叶变换对表明，如果一个时域信号x(t)有一个傅立叶变换X(f)，那么这个时域信号x(t)e^(j2Piat)将存在傅立叶变换X(f-a)。因此，测量的时域信号通过乘以指数项e^(j2Piat)，那么，信号的频谱将向下移动到f-a。 通过一个实例，表明这个变换过程。我们有一个信号，是按10KHz采样得到的，因此，这个信号对应的频率范围为0≤f≤5KHz。我们将细化的频率范围为1900≤f≤2100Hz，FFT变换样本点数为1024。 整个变换过程步骤如下：定义要进行分析的频率范围1900≤f≤2100Hz的中心频率fc=2000Hz；整个测量的时域信号乘以^(j2Pifct)，注意这将产生一个复数信号。这一过程同时使频率移动到-100≤f≤100Hz。对这个频率发生移动的信号的实部和虚部施加一个低通滤波器，带宽为100Hz。对上一步低通后的信号进行抽样，每25个点抽样一个（5000/200=25）。将抽样后的实部和虚部再组合成一个复数信号。对这个复数信号按每帧1024个样本点进行FFT变换。将负频率移动到频谱的下半段。 注意到zoomFFT处理并没有违背频谱分析这个重要的关系：时域数据块的时间长度等于频率分辨率的倒数：T=1/∆f。在第4步中，对原始数据进行了抽样，因此，我们不得不使用25倍原来长度的时域信号才能保持1024个样本点。 为了获得相同的频率分辨率，另一种可行的办法是使用更大的数据点N=25*1024。对于大数据块进行FFT，早期是很难实现的，现今实现起来可能会容易些。虽然现在很少用到zoomFFT，但它仍有使用价值与作用。 当用1024个样本点对原始信号作FFT时，其频率分辨率为9.Hz，而使用zoomFFT，相应的频带的频率分辨率为原来的1/25，为0.Hz，频率分辨率提高了25倍。 因此，zoomFFT明显提高了频率分辨率。 ZoomFFT 不如 chirp Z 变换 今天看到这个“算法”，感觉智商受到了侮辱。 首先要明确，“频谱”的精度或者“分辨率”收两个因素限制，一个是数据源精度，一个是FFT精度。 Zoom FFT提升的是FFT精度或者FFT分辨率，和插值效果是一样的，不能改变数据源分辨率。 在一般场景下，FFT点数的选择都应保证FFT底噪远低于数据，这种常见下zoomfft是没用的。 在一些特殊情况，比如FFT点做不了这么多，或者硬件限制FFT噪声大于数据了，那这种方式是有效的。
2024最新激活全家桶教程，稳定运行到2099年，请移步至置顶文章：https://sigusoft.com/99576.html
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请联系我们举报，一经查实，本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处：https://sigusoft.com/20917.html
