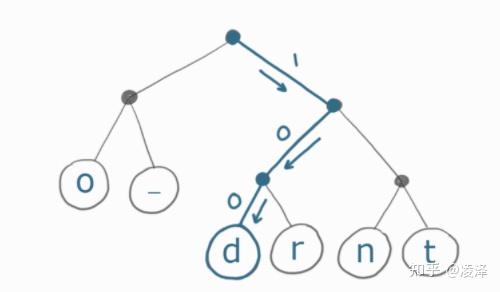
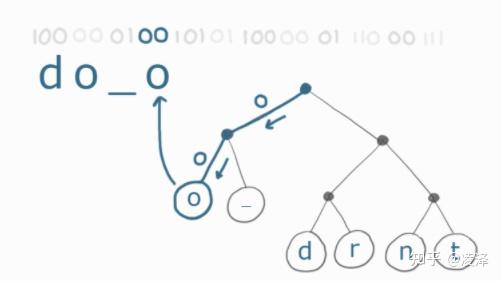
快速理解Huffman Coding(霍夫曼编码) 压缩 假设我们想压缩一段字符串 (哈夫曼编码可以压缩任意数据，本文只是讲解基本原理，选用字符串最容易理解) 通常一段文本中，有些字符出现的频率会比另外一些字符更高；而哈夫曼编码就正是利用了这一点，对这段文本中出现的全部字符重新编码，让出现频率更高的字符占用更少的空间从而达到压缩的目的 就用 Yoda 大师的经典名言 “do or do not” 来当作示例，这句话一共 12 个字符。按照计算机默认编码格式 (关于编码格式，你可以参考UTF百科)，每个英文字符占用 8 比特 (bit) , 一共占用96比特 ；那么采用霍夫曼编码以后一共占用多少比特呢？ 先构建哈夫曼树。出现频率最高的字符，就距离树的根节点最近。依次类推，下图就是字符串 “do or do not” 的哈夫曼树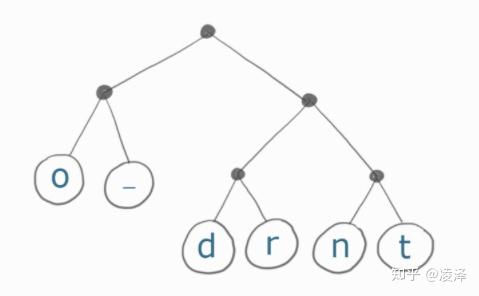
最常见的字符 ‘o’和 ‘ ‘ (空格) 距离根节点只有 2 步，而最不常见的 t 则距离根节点有 3 步。哈夫曼编码最神奇的事情来了，我们存储的不再是字符本身，而且存储从根节点到达它的路径。具体什么意思呢？ 我们从根节点开始，然后沿着树像要编码的字符前进。如果走了左侧路径，则标记为 0，走了右侧路径，我们则标记为 1 
因此，字符 d 的编码为：’100′ ，而字符 d 的默认编码是：’ 0 ‘，整个字符串编码以后的结果如下： 
最终需要消耗 96 比特的字符串，采用哈夫曼编码以后，只需要 29 字节，足足压缩了2/3 解压 怎么解压呢？就是照着存储路径，依次从哈夫曼树拿到该路径对应的真实字符 
聪明的你是不是早已想到，如果我只把压缩后的数据发给别人，别人没有对应的哈夫曼树，就没法解压。是的，大概来说有 3 种办法：将哈夫曼树和压缩后的文本一起发给对方，就可以根据你发的哈夫曼树来解压可以双方都同意同一颗已知的哈夫曼树，压缩和解压就可以都用它发送足够的信息，对方可以根据这些信息构建出哈夫曼树从而达到解压的目的（Gzip的工作方式），但是请注意：同样的信息，也有可能构建出不同的哈夫曼树，因此发送的信息要确保构建的哈夫曼树一致
2024最新激活全家桶教程，稳定运行到2099年，请移步至置顶文章：https://sigusoft.com/99576.html
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请联系我们举报，一经查实，本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处：https://sigusoft.com/20576.html
