确定策略梯度DPG可用于解决连续控制问题

我们考虑机械臂连续控制问题,机械手臂有两个可以运动的关节,所有有两个变量,自由度等于2。动作空间是二维的,有无穷多个动作。
DPG是2014年提出的,两年后出现了将它用到神经网络中,出现了DDPG。
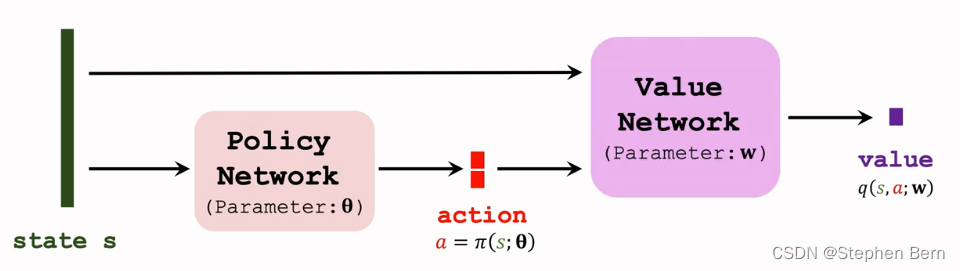
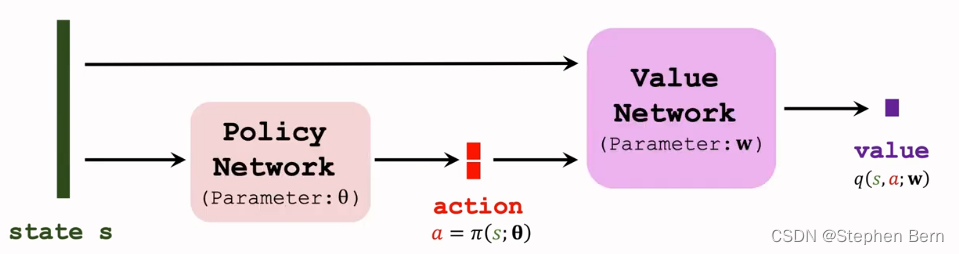
DPG是一种Actor-Critic方法,有一个策略网络,和一个价值网络。
策略网络控制agent做运动,所以它叫做actor,它根据状态s做出动作a;价值网络不控制agent,它根据状态s给动作a打分,从而指导策略网络做出改进,所以价值网络叫做critic。
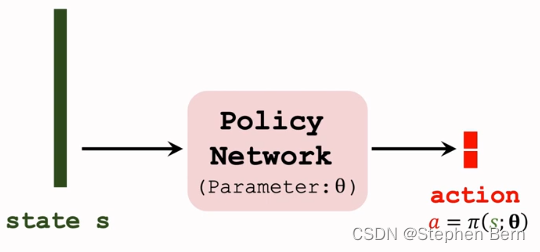
- Use a deterministic policy network (actor): a = π ( s ; θ ) a=\pi(s;\theta) a=π(s;θ).
策略网络是确定性的函数,记作 π ( s ; θ ) \pi(s;\theta) π(s;θ), θ \theta θ是神经网络的参数。策略网络也被成为actor,因为决策是由它做的。
它的输入是状态s,它的输出不是概率分布,而是一个具体的动作a。给定状态s,输出的动作是确定的,没有随机性,这就是为什么叫determistic。策略网络的输出可以是实数,也可以是向量,例如上述机械臂例子中,输出的动作是一个二维的。
\;\;\;\;\;\;\;
- Use a value network (critic): q ( s , a , w ) q(s,a,w) q(s,a,w).
价值网络也叫做critic,记作 q ( s , a , w ) q(s,a,w) q(s,a,w),w是价值网络的参数。价值网络有两个输入参数,一个是状态s,另一个是动作a。基于状态s,价值网络评价动作a的好坏程度。
\;\;\;\;\;\;\;
- The critic outputs a scalar that evaluates how good the action a a a is.
价值网络的输出是一个实数,这个实数是对动作好坏的评估,动作越好,这个实数越大。
我们要训练两个神经网络,让两个网络共同进步,让策略网络越来越好,让价值网络打分越来越准确。
接下来我们看如何训练这两个神经网络。
Updating Value Network by TD
先来用TD算法更新价值网络。
-
Transition: ( s t , a t , r t , s t + 1 ) (s_t,a_t,r_t,s_{t+1}) (st,at,rt,st+1).
每次观测到的transition就是一条训练数据。 -
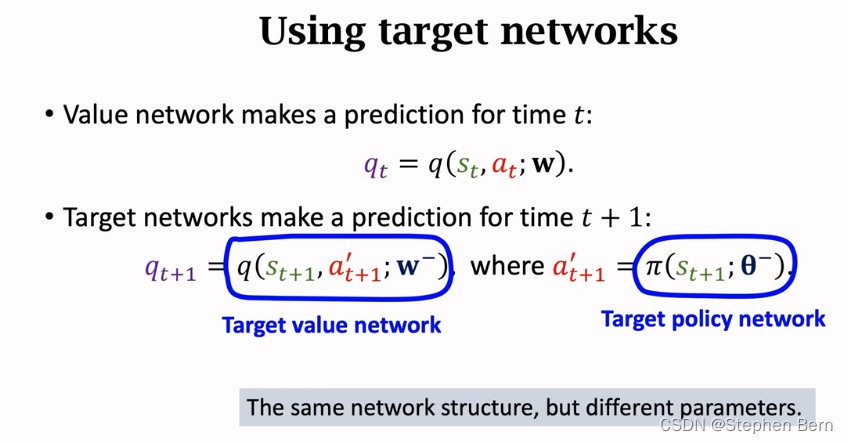
Value network makes prediction for time t t t:
q t = q ( s t , a t ; w ) . q_t=q(s_t,a_t;w). qt=q(st,at;w).
让价值网络预测 t \,t\, t时刻的动作价值,记作 q t q_t qt。 -
Value network makes prediction for time t + 1 t+1 t+1:
q t + 1 = q ( s t + 1 , a t + 1 ’ ; w ) , w h e r e a t + 1 ‘ = π ( s t + 1 ; θ ) . q_{t+1}=q(s_{t+1}, a_{t+1}^’; w), where \;a_{t+1}^‘=\pi(s_{t+1};\theta). qt+1=q(st+1,at+1’;w),whereat+1‘=π(st+1;θ).
再让价值网络预测 t + 1 t+1 t+1时刻的动作价值。我们知道t+1时刻的状态 s t + 1 s_{t+1} st+1,把 s t + 1 s_{t+1} st+1输入策略网络 π \pi π算出下一个动作,记作 a t + 1 ‘ a_{t+1}^‘ at+1‘,这个动作并不是agent真正执行的动作, a t + 1 ‘ a_{t+1}^‘ at+1‘只是用于更新价值网络而已。把 s t + 1 , a t + 1 ‘ s_{t+1},a_{t+1}^‘ st+1,at+1‘输入价值网络,算出t+1时刻的动作价值,记作 q t + 1 q_{t+1} qt+1。 -
TD error: δ t = q t − ( r t + γ ⋅ q t + 1 ) . \delta_t=q_t-(r_t+\gamma·q_{t+1}). δt=qt−(rt+γ⋅qt+1).
( r t + γ ⋅ q t + 1 ) (r_t+\gamma·q_{t+1}) (rt+γ⋅qt+1)该部分为TD Target,它一部分是真实观测到的奖励 r t r_t rt,另一部分是价值网络做出的预测 q t + 1 q_{t+1} qt+1。我们认为TD Target比单纯的预测 q t q_t qt更接近真相,所以鼓励 q t q_t qt接近TD Target,也就是让TD error尽量小。 -
Update: w ⟵ w − α ⋅ δ t ⋅ ∂ q ( s t , a t ; w ) ∂ w w \longleftarrow w-\alpha·\delta_t·\frac{\partial q(s_t,a_t;w)}{\partial w} w⟵w−α⋅δt⋅∂w∂q(st,at;w).
这样做梯度下降,可以让 δ t \delta_t δt的平方减小,也就是说让价值网络的预测更接近target。
\;\;\;\;\;\;\;
Updating Policy Network by DPG
学习策略网络需要用到确定策略梯度。
策略网络根据输入的s来计算动作a,从而控制agent运动。
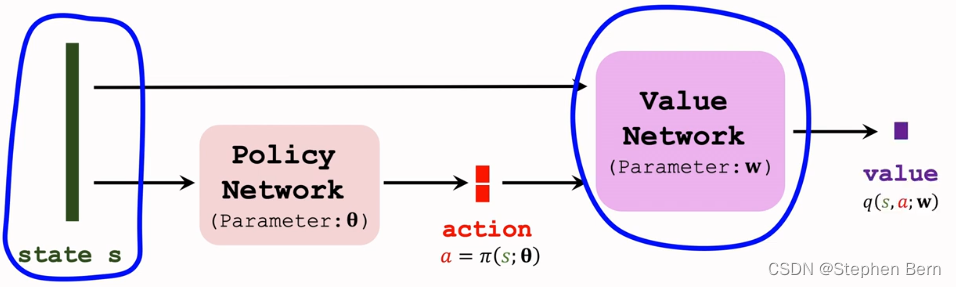
- The critic q ( s , a ; w ) q(s,a;w) q(s,a;w) evaluates how good the action a a a is.
训练策略网络要靠价值网络的帮忙,价值网络可以评价做出动作a的好坏,从而指导策略网络做出改进。 - Improve θ \theta θ so that the critic believes a = π ( s ; θ ) a=\pi(s;\theta) a=π(s;θ) is better.
策略网络的参数是 θ \theta θ, θ \theta θ越好,那么决策就越正确,输出的动作a就越好,策略网络自己不知道动作的好坏,好坏全靠价值网络的评价。 - Update θ \theta θ so that q ( s , a ; w ) = q ( s , π ( s ; θ ) ; w ) q(s,a;w)=q(s,\pi(s;\theta);w) q(s,a;w)=q(s,π(s;θ);w) increase.
价值网络的输出越大,就意味着动作越好。所以我们要改进策略网络中的 θ \theta θ,让价值网络的输出越大越好。 - Goal: Increasing q ( s , a ; w ) , w h e r e a = π ( s ; θ ) q(s,a;w), where\; a=\pi(s;\theta) q(s,a;w),wherea=π(s;θ).
综上,训练策略网络的目标,是为了让价值网络的q值变大。价值网络的输入时状态s和动作a,动作a是由策略网络 π \pi π算出来的,对于确定的状态s,策略网络会输出确定的动作a。
\;\;\;\;\;\;\;
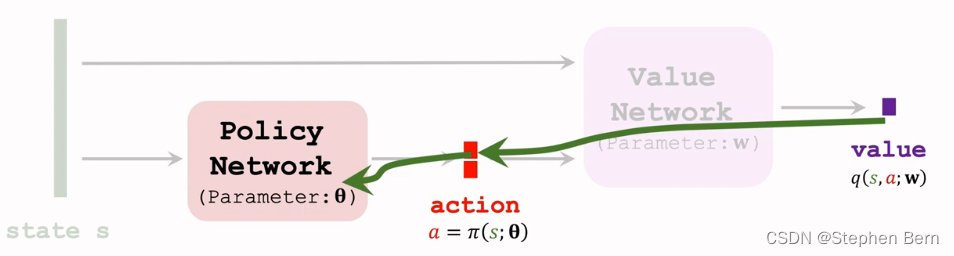
如果输入的状态是固定的,而且价值网络也是固定的,那么唯一会影响价值q的因素,就是策略网络的参数 θ \theta θ。我们想要更新 θ \theta θ,使得价值q变大。所以我们计算q关于 θ \theta θ的梯度,然后做梯度上升,更新 θ \theta θ,这样可以让价值q变大。
这个梯度就叫做确定策略梯度DPG,它是价值q关于策略网络参数 θ \theta θ的梯度。可以拿链式法则来计算梯度,梯度等于动作a关于 θ \theta θ的导数乘以q关于a的导数。其实就是让梯度从价值q传播到动作a,然后再从a传播到策略网络。
\;\;\;\;\;\;\;
- Gradient ascent: θ ⟵ θ + β ⋅ g \theta\longleftarrow\theta+\beta·g θ⟵θ+β⋅g.
最后做梯度上升来更新, β \beta β是学习率。这样更新 θ \theta θ可以让价值变大,也就是说价值网络认为策略变得更好。
Improvement: Using Target Network
用刚才的算法训练价值网络,效果不是太好,可以用一些技巧来改进,比如Target Network。Target Network也可以改进DQN的训练。
首先回顾之前价值网络的训练。
\;\;\;\;\;\;\;
在训练DQN的时候做Bootstrapping,会造成偏差,偏差一定是高估。
把Bootstrapping用到这里也会出现偏差,偏差未必是高估,也可能是低估。如果初始的时候是高估,那么就一直会是高估,如果初始时是低估,就一直会是低估。原因是这样的,假如一开始有低估,那么TD Target就会有低估,然后低估就会被传播到价值网络自身,导致低估一直存在。
Bootstrapping就会有这个毛病,解决方案就是用不同的网络来计算TD target,尽量避免Bootstrapping,这样可以让性能稳定很多。
Computing TD Target using Target network
\;\;\;\;\;\;\;
\;\;\;\;\;\;\;
\;\;\;\;\;\;\;
仔细观察,更新target network用到了策略网络和价值网络,所以target network的参数还是依赖于策略网络和价值网络,用target network算出的TD Target还是跟策略和价值网络有关,因此用target network依然会出现Bootstrapping,当然用target network总比不用要好。
其他方法让训练做的更好,他们也可用于DPG。
\;\;\;\;\;\;\;
Stochastic Policy VS Deterministic Policy
\;\;\;\;\;\;\;
2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/169258.html