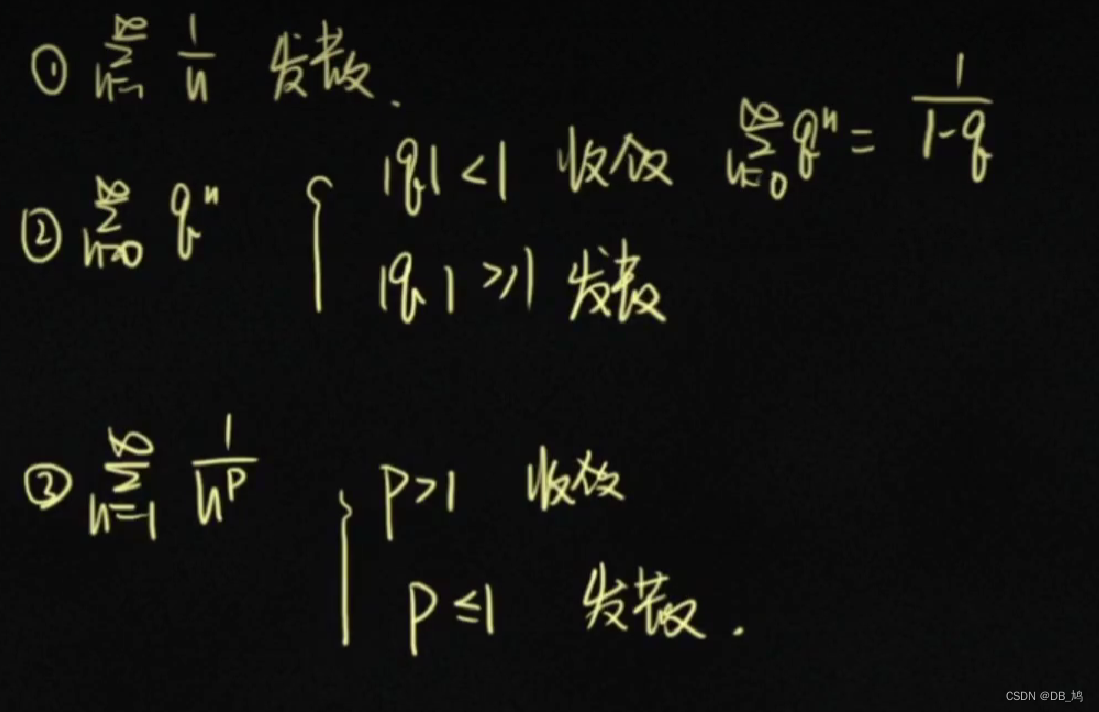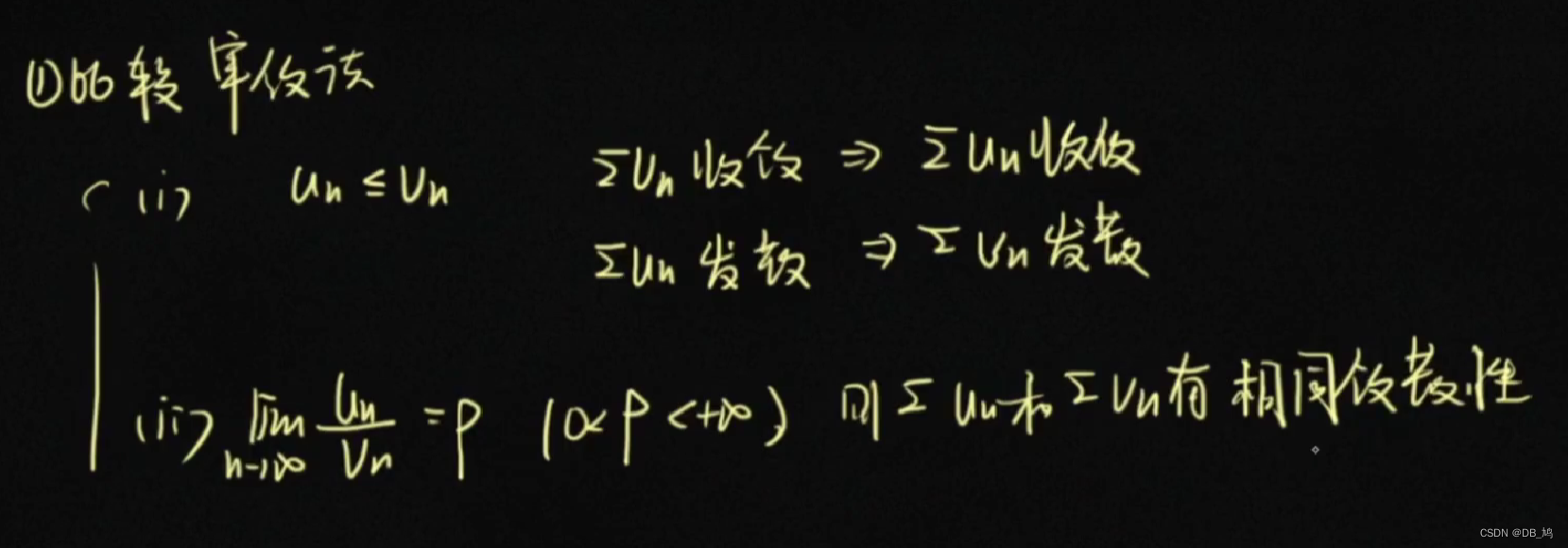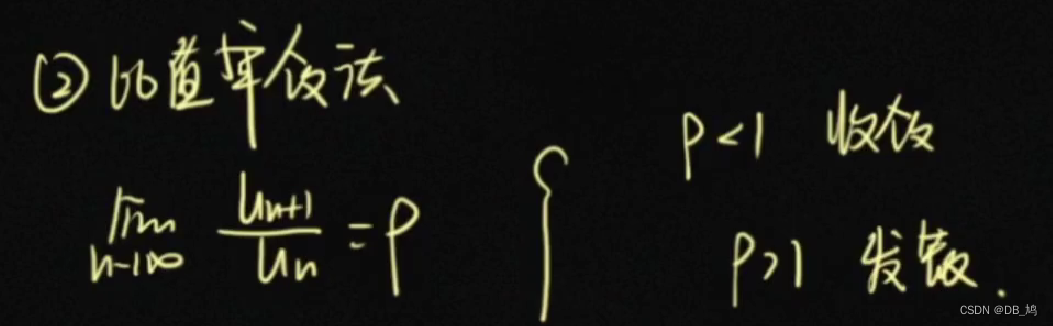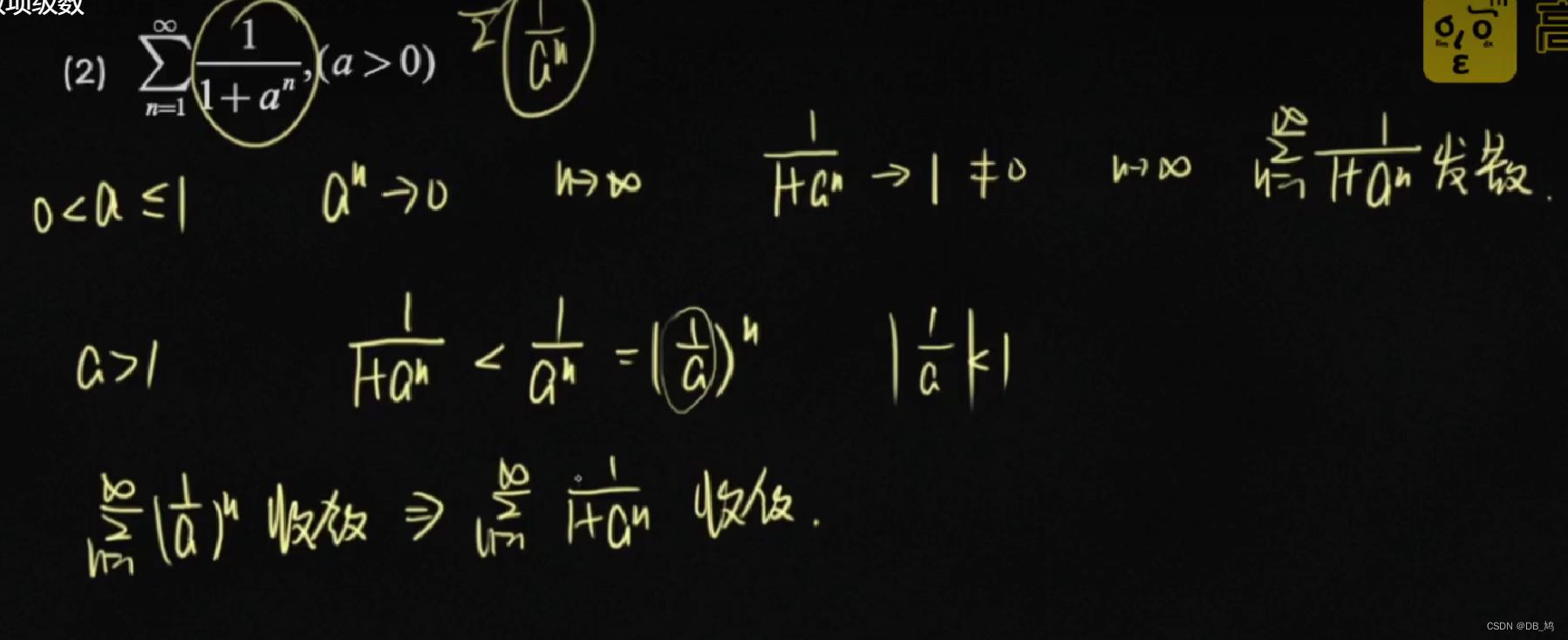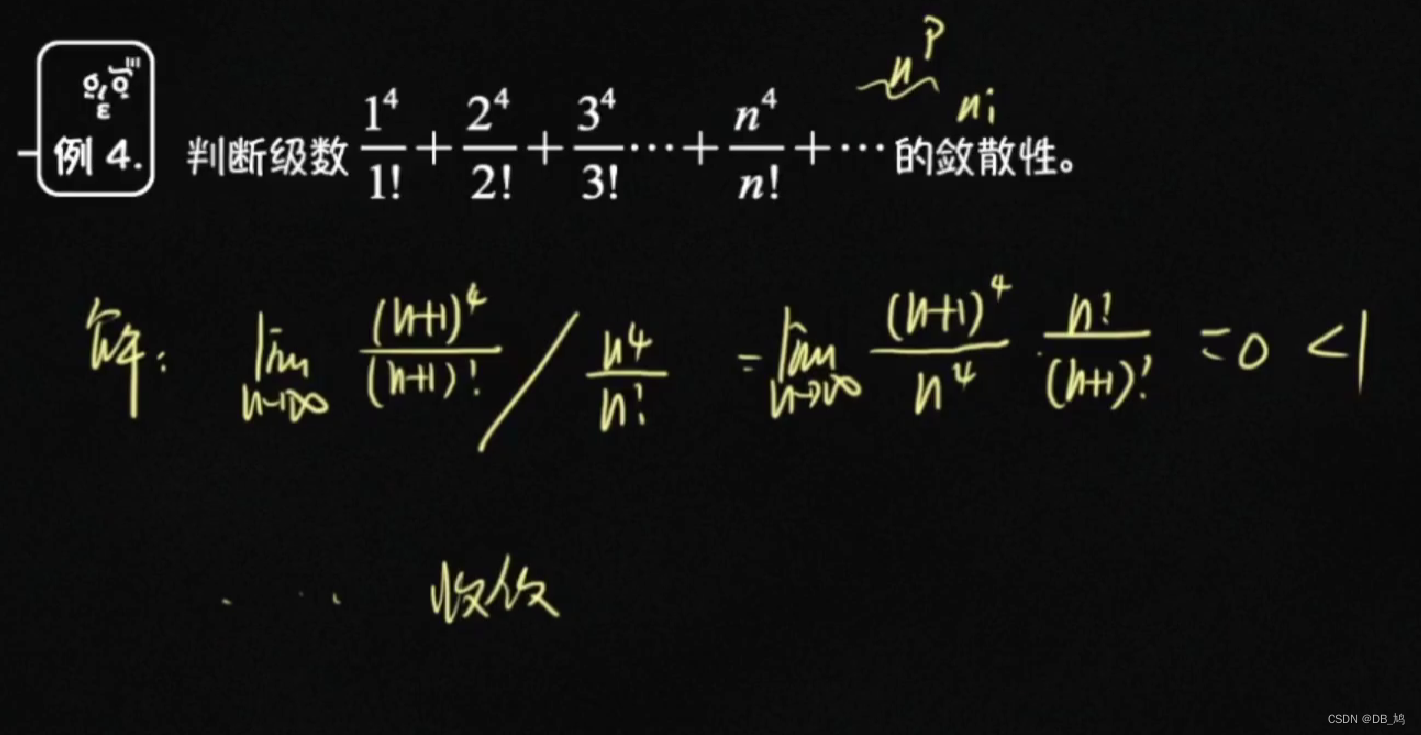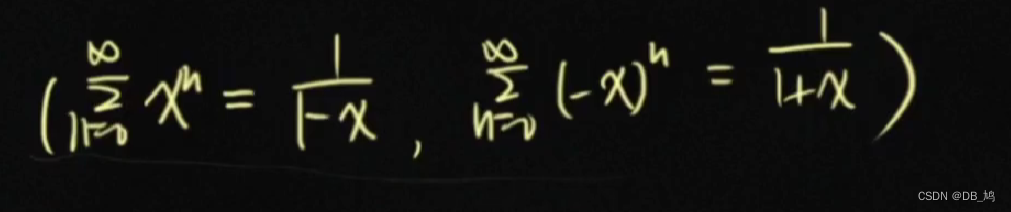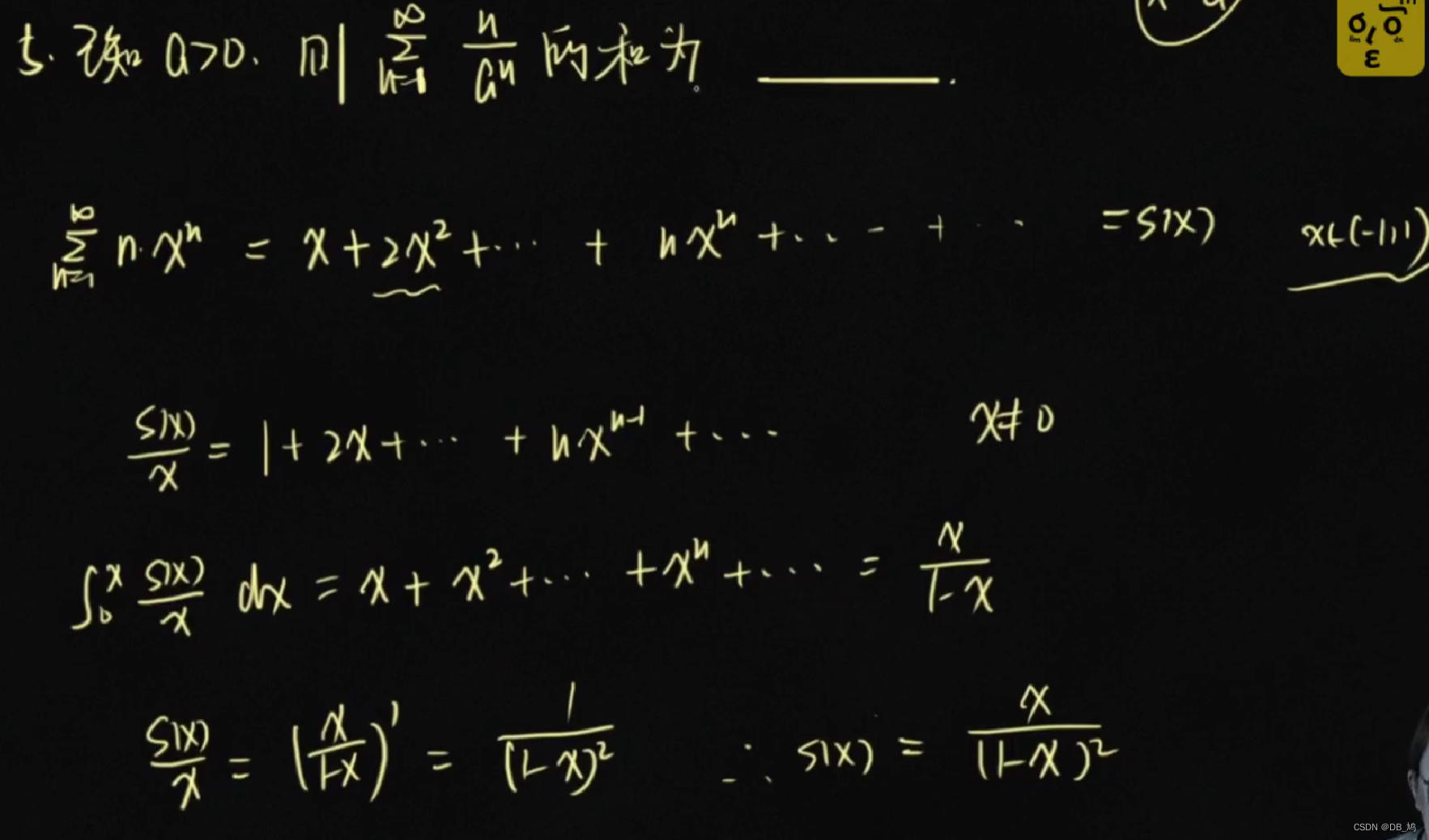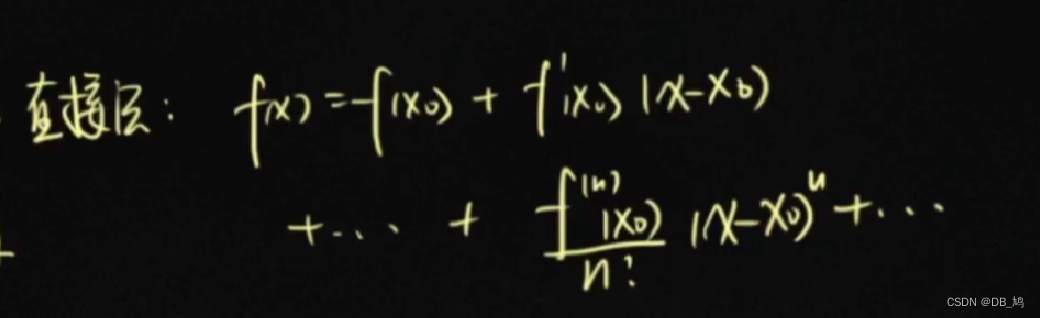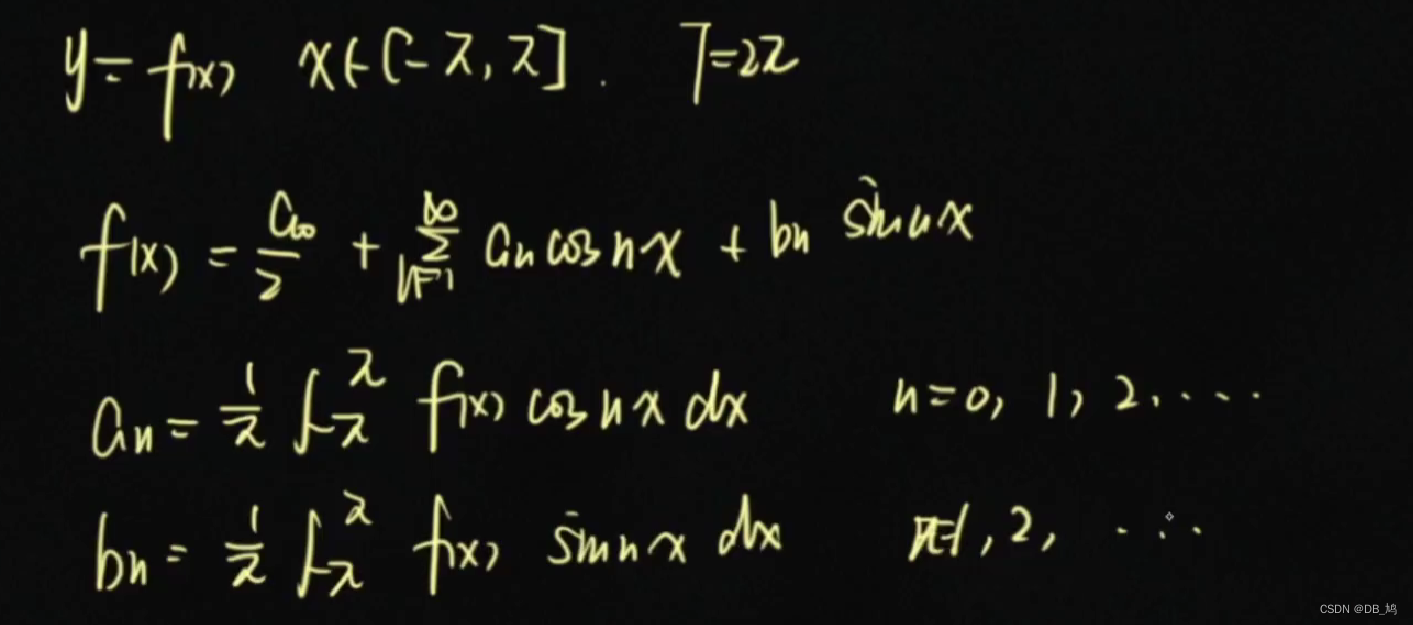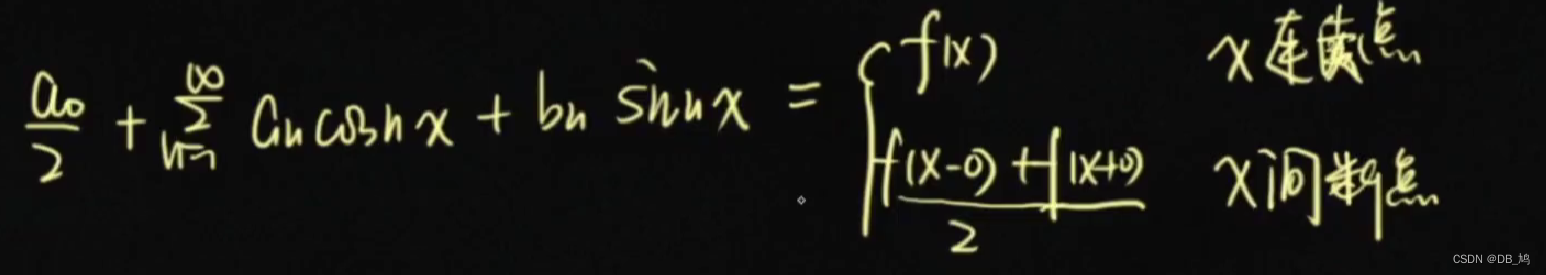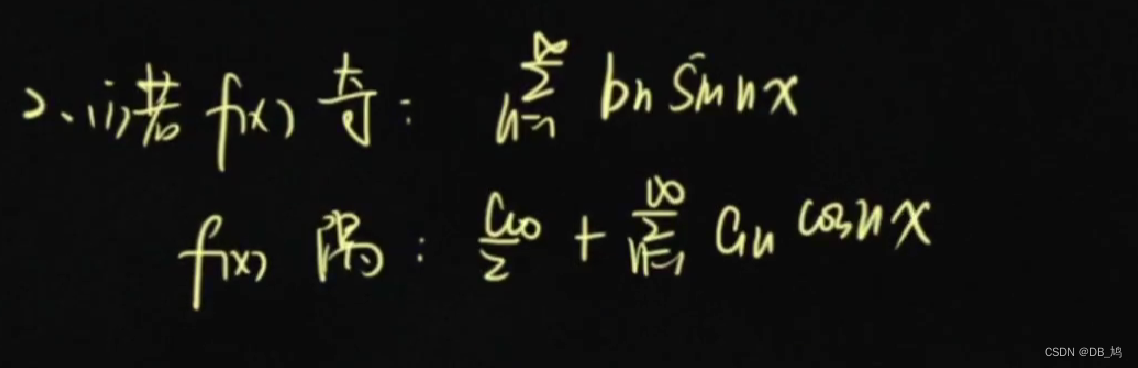1. 激活谷首页
  2. 激活谷笔记

高数—级数_高数基本极限公式大全

• 激活谷笔记

高数—级数_高数基本极限公式大全

常数项级数

定义

先搞清什么是级数，级数是一个求和，可以先理解为是数列的求和。

这样一个级数： ∑ n = 1 ∞ f ( n ) = f ( 1 ) + f ( 2 ) + f ( 3 ) + . . . + f ( n ) + . . . \sum_{n=1}^\infty f(n) = f(1) + f(2) + f(3) + … + f(n) + … ∑n=1∞​f(n)=f(1)+f(2)+f(3)+…+f(n)+…

S ( n ) = f ( 1 ) + f ( 2 ) + f ( 3 ) + . . . + f ( n ) S(n) = f(1) + f(2) + f(3) + … + f(n) S(n)=f(1)+f(2)+f(3)+…+f(n) 叫做部分和

如果 lim ⁡ n → ∞ S ( n ) = S ( 常数 ) \lim\limits_{n\to\infty} S(n) = S(常数) n→∞lim​S(n)=S(常数)，那么级数收敛。

使用定义法判断敛散性要学会的计算方法

  • 数列求和
  • 求极限

性质

  1. 如果 ∑ n = 1 ∞ f ( n ) = S \sum_{n=1}^\infty f(n) = S ∑n=1∞​f(n)=S ，则 ∑ n = 1 ∞ k f ( n ) = k S \sum_{n=1}^\infty kf(n) = kS ∑n=1∞​kf(n)=kS
  2. 如果 ∑ n = 1 ∞ f 1 ( n ) = S 1 ， ∑ n = 1 ∞ f 2 ( n ) = S 2 \sum_{n=1}^\infty f1(n) = S1，\sum_{n=1}^\infty f2(n) = S2 ∑n=1∞​f1(n)=S1，∑n=1∞​f2(n)=S2 ，则 ∑ n = 1 ∞ f 1 ( n ) + f 2 ( n ) = S 1 + S 2 \sum_{n=1}^\infty f1(n)+f2(n) = S1+S2 ∑n=1∞​f1(n)+f2(n)=S1+S2
  3. 如果 ∑ n = 1 ∞ f 1 ( n ) 收敛， ∑ n = 1 ∞ f 2 ( n ) 发散 \sum_{n=1}^\infty f1(n) 收敛，\sum_{n=1}^\infty f2(n) 发散 ∑n=1∞​f1(n)收敛，∑n=1∞​f2(n)发散 ，则 ∑ n = 1 ∞ f 1 ( n ) + f 2 ( n ) 发散 \sum_{n=1}^\infty f1(n)+f2(n) 发散 ∑n=1∞​f1(n)+f2(n)发散
  4. 如果 ∑ n = 1 ∞ f 1 ( n ) 发散， ∑ n = 1 ∞ f 2 ( n ) 发散 \sum_{n=1}^\infty f1(n) 发散，\sum_{n=1}^\infty f2(n) 发散 ∑n=1∞​f1(n)发散，∑n=1∞​f2(n)发散 ，则 ∑ n = 1 ∞ f 1 ( n ) + f 2 ( n ) 收敛性不确定 \sum_{n=1}^\infty f1(n)+f2(n) 收敛性不确定 ∑n=1∞​f1(n)+f2(n)收敛性不确定
  5. 如果 ∑ n = 1 ∞ f ( n ) 收敛 \sum_{n=1}^\infty f(n) 收敛 ∑n=1∞​f(n)收敛 ，则 lim ⁡ n → ∞ f ( n ) = 0 \lim\limits_{n\to\infty} f(n) = 0 n→∞lim​f(n)=0
  6. 如果 lim ⁡ n → ∞ f ( n ) = 0 \lim\limits_{n\to\infty} f(n) = 0 n→∞lim​f(n)=0，不一定 ∑ n = 1 ∞ f ( n ) 收敛 \sum_{n=1}^\infty f(n) 收敛 ∑n=1∞​f(n)收敛
  7. 如果 lim ⁡ n → ∞ f ( n ) ≠ 0 \lim\limits_{n\to\infty} f(n) \not= 0 n→∞lim​f(n)=0，则 ∑ n = 1 ∞ f ( n ) 发散 \sum_{n=1}^\infty f(n) 发散 ∑n=1∞​f(n)发散

常用级数的敛散性

在这里插入图片描述

正项级数审敛法

级数中的每一项都大于0的叫做正项级数。

比较法

  1. 大级数收敛，则小级数收敛
  2. 小级数发散，则大级数发散
  3. 两个级数的比值为常数（0， + ∞ +\infty +∞），则两个级数的敛散性相同
    在这里插入图片描述

比值法

当n趋向无穷大时，有后一项与前一项比较得出一个数s。
如果s小于1，则级数收敛；
若s大于1，则级数发散。
在这里插入图片描述

例题

  1. 比较法两种解法
    在这里插入图片描述
  2. 利用性质7、常用级数和比较法
    在这里插入图片描述
  3. 比值法
    在这里插入图片描述
  4. 比值法
    在这里插入图片描述

交错级数审敛法

级数中各项为正负交错称为交错级数

莱布尼兹定理

使用莱布尼兹定理：

对于这样一个级数： f ( n ) = ( − 1 ) − 1 u ( n ) f(n) =(-1)^{-1}u(n) f(n)=(−1)−1u(n)
在不考虑符号的情况下，u(n)单调递减且 lim ⁡ n → ∞ f ( n ) = 0 \lim\limits_{n\to\infty} f(n) = 0 n→∞lim​f(n)=0，则交错级数收敛

绝对收敛和条件收敛

在级数收敛的前提下分为绝对收敛和条件收敛

如果级数的公式加绝对值后求级数依然收敛，那么称为绝对收敛。
如果加绝对值之后变为发散，则称为条件收敛。

例题

在这里插入图片描述

解题过程

  1. 先判断是不是绝对收敛
  2. 判断是不是条件收敛
  3. 都不是就是发散的

在这里插入图片描述

幂级数

常数项级数的每一项都是函数，幂级数的每一项都是函数，一般都是幂函数，所以称为幂级数。

∑ n = 1 ∞ f n ( x ) = a n ( x − x 0 ) n \sum_{n=1}^\infty f_n(x) = a_n(x-x_0)^n ∑n=1∞​fn​(x)=an​(x−x0​)n

收敛半径、收敛区间、收敛域

  • 收敛半径： R = lim ⁡ n → ∞ ∣ a n a n + 1 ∣ R = \lim\limits_{n\to\infty} | \frac{a_n}{a_{n+1}}| R=n→∞lim​∣an+1​an​​∣
  • 收敛区间： ( − R ， R ) (-R，R) (−R，R)
  • 收敛域：讨论当x = ± R \pm R ±R时对应的常数项级数的敛散性，收敛这则一端为闭区间，发散则这一端为开区间

例题
在这里插入图片描述

求和

求和的结果称为和函数

  1. 重要的公式
    在这里插入图片描述
  2. 求解方法：代数变换、求导和积分
    在这里插入图片描述
  3. 例题

记得先求收敛域，收敛域就是和函数的定义域

在这里插入图片描述

进行适当的代数变换

在这里插入图片描述

展开

  1. 直接法：公式法
    在这里插入图片描述

  2. 间接法：傅里叶展开
    在这里插入图片描述

  3. 例题
    在这里插入图片描述

傅里叶级数

函数展开

展开公式
在这里插入图片描述
求和公式
在这里插入图片描述

正弦、余弦级数

在这里插入图片描述

2024最新激活全家桶教程，稳定运行到2099年，请移步至置顶文章：https://sigusoft.com/99576.html

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请联系我们举报，一经查实，本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处：https://sigusoft.com/168331.html

赞 (0)
0
上一篇 2024年 7月 2日 下午2:08
下一篇 2024年 7月 2日

相关推荐

关注微信