沙漠掘金获胜方法_博弈论考试题及答案pdf

摘要
穿越沙漠游戏是一个由单人或多人玩家在一定的游戏参数设定之下，综合考虑行走路径，移动策略以及购买策略以实现最终收益最大化的项目，本文主要从最优移动策略的性质出发讨论如何快速计算寻找所有可能路径，以及对于确定路径计算最优购买方案，建立了数学模型求解决策。
针对问题一，确定在单人参与天气已知的情况下的最佳游戏策略。该问题主要需要确定玩家所选取的移动路线以及是否进行挖矿，如何采购食物和水及分配比例的问题，在对问题的分析当中，我们将所有的区域按照玩家在该区域当中是否能进行购买以及挖矿行为分成关键点以及平凡点，确定了最优路线的存在性，并讨论且证明了最优路径所必然具有的六条性质。最优路径必然将在一个四阶非完全图中求得，为了求出所有满足性质的路径，我们根据玩家在不同的关键点区域所能进行的不同的移动策略和购买挖矿策略，建立了相应的转移方程。通过特殊性质的限制，建立了一颗相应的决策树，并完成了对于决策树的剪枝。利用深度优先搜索算法，遍历了所有可能的决策方案，并对每一种方案计算其最优的购买方案，以及最终所能获得的收益。通过比较所有可能路径的收益，最终确定使得收益最大化的路径。以到达最后目标位置收益最大为目标进行计算，可得到对于第一关玩家策略为花费24天时间抵达终点，最终收益10470。对于第二关玩家策略为花费30天时间抵达终点，最终收益12195。
针对问题二，确定在单人参与天气未知的情况下的最佳游戏策略，此时天气虽然未知，但可以将其考虑为具有一定概率的分布。我们先行讨论概率分布的可能情况，全场游戏的天气整体可视为马尔可夫过程，当马尔可夫过程转移趋于稳态时，具体某一天的天气具有确定的概率分布。我们以期望最大化建立了相关的优化模型。给出了对于马尔可夫过程转移趋于稳态时不同的状况，玩家可以选取的策略。
针对问题三，在多人参与天气已知和多人参与天气未知的情况下进行游戏策略选择，对于第五关双人参与天气已知，此时问题满足静态平衡博弈，问题是一个不完全信息静态博弈。在一个静态有限Bayes博弈中，存在纳什均衡，因此确认第五关中均衡的存在性，我们讨论了单个博弈者所可以选取的策略，利用Harsany转换，我们最终确定的两位参与者所能达到的均衡状态。对于第六关，参与博弈人数上升，但本身满足均衡存在性定理，但此时天气未知需要进行多阶段博弈分析，考虑到多阶段博弈可能存在的信任问题，我们对三人情况进行了局部分析，最终得到了改进情况下的Bayes—Nash均衡。

关键字：博弈论；深度优先搜索；状态转移；最优策略；优化模型
一、问题重述
对如下游戏进行研究：玩家初始情况下拥有地图以及初始资金，初始资金可用于换取水和食物，从起点出发，在终点结束游戏。途中可能遇到不同天气以及地形，目标是在规定时间内前往终点， 并赚取尽可能多的金钱。
其中基本规则有：存在时间限制，超出限制为失败；存在负重上限不得携带超出负重上限的水和食物；矿山可以产生基础收益；行走会消耗两倍基础消耗；天气有沙暴，晴天，高温，分别产生不同的基础消耗；挖矿需要消耗三倍的基础消耗，沙暴天不能行走；村庄会以两倍基础价格出售水和食物。
需要解决的问题：
1.在只有一名玩家并且给定天气的情况下求解第一张以及第二张地图。
2.在只有一名玩家诞生天气未知的情况下求解第三张以及第四张地图
3. 在有n名玩家的情况下，已知n名玩家在同一位置时会使得消耗变为n倍挖矿产出减少n倍，并且村庄售价变为4倍。求解第五张以及第六张地图。

二、问题分析
2.1问题一分析
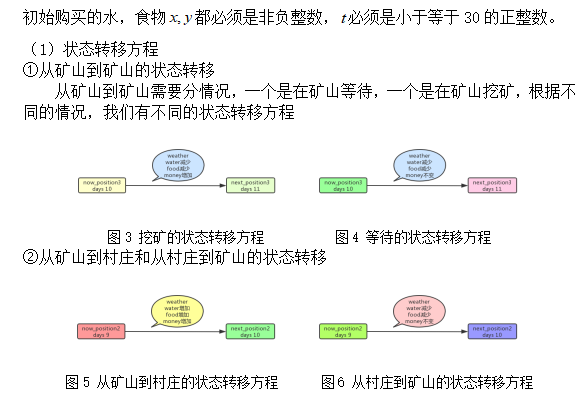
问题一希望在游戏过程中的天气全部已知的情况下，求解出玩家可以保留或者赚到更多资金的最优穿越沙漠策略，并且求出该策略下，我们选取的最优路径上每天消耗的水和食物，以及求出最终的收益。收益表示为玩家自身带的资金+穿越沙漠时赚的钱-穿越沙漠时在起点或者村庄购买的水和粮食的钱+到达终点后将剩余的水和食物卖出去的钱。在这里，玩家自身带的资金为一个确定值，并且由于我们知道每一天的天气，因此我们可以通过控制在村庄或者起点购买水和食物的量，来使得到达终点的剩余水和食物为0（因为卖出剩余水和食物只能收益其售价一半的钱，因此，最终剩余为0是收益最大的一个必要条件），因此我们的主要目标为：穿越沙漠时赚的钱最多，穿越沙漠时消耗的水和食物最少。由于第一关中，挖矿的基础收益为1000，而即使是沙暴天气，挖矿消耗是基础消耗三倍的情况下，挖矿仍然是赚的，因此我们要在保证水和食物是可以满足需要的情况下，尽可能的在矿山挖矿，然后再去村庄补充资源，再回去。
主要目标确定后，开始编写寻找所有可能路径的代码，将所有可以在30天内走到终点的路径寻找出来，然后建立相应的优化模型，写出约束条件，然后使用check函数实现约束条件，将不符合约束条件的路径的最终收益记为0，check函数里面主要实现约束条件的思路是：先将点区分开来，分为关键点和平凡点，将图简化为4个关键点组成的图，然后把可补给点：起点和村庄标记出来，那么我们只需要判断路径在两个可补给点点之间所消耗的水，食物的重量是否满足约束条件，水的重量+食物的重量效益等于1200kg，然后在判断可挖矿点之间的钱是否恒大于等于0，如果满足，那么就是可行路径，然后我们算出所有可行路径的收益，最终，把收益最大的路径保留下来，作为我们的优化结果。
对于第二关，本题的主函数可以说是没有变化的，只需要修改关键点，平凡点，可补给点，可挖矿点即可，即将简化的图更新即可，然后和第一关一样，可以找到最终的优化的结果。
对于一，二两关，由于天气，地图，收益等条件都是已知的，所以我们大胆判断，对于一二两关来说，是有确定解的，因此可以通过检验第一二问的答案，来判断我们的模型的准确性和可行性。
2.2问题二分析
对于问题二而言，在规则上发生的变化主要在于两点，一是玩家不再预先知道全部的天气，必须实时根据当天天气做出决策。二是第三关与第四关与前两关的主要区别还包括了晴天与高温天气所产生的消耗以及挖矿所得到的基础收益等参数发生了数值的改变，使得我们在问题一中所建立的部分引理的正确性，不再成立。

2.3问题三分析
在问题三的情形下，该游戏变为一个多人游戏，并且经研究可以发现，任何一个玩家的行动对于其他玩家均是没有益处的（甚至可能是有害的），因此我们认为这是一个将它当成一个多人对抗的模型，使用寻找Bayes-Nash均衡点的方法处理此题；而不是将其作为一个合作博弈的模型，求解它的Pareto最优解。地图五为一个双人不完全信息静态博弈，地图六是一个三人不完全信息动态博弈，都可以使用Harsany转换将其转换为双人完全但不完美信息动态博弈和三人完全但不完美信息动态博弈。而地图五是双人情况是一个对称情况，我们的结果可以不用概率优化最大值求解，而是通过分析直接求解最优的双人路径。由于第六关也可以看成无次序的选择，因此也可以简化成一个同时选择的完全但不完美信息动态博弈，由于存在决策回合问题（就是可以多段式选择各自的行动），可以进而根据其类别带入信号博弈模型中求解，从而简化并求解模型。

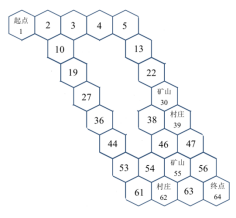
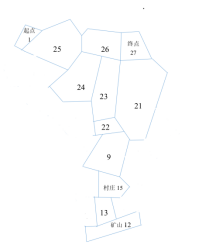
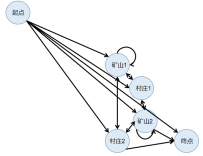
图1 第一关的模型 图2第二关的模型
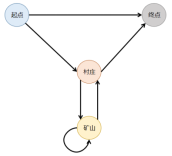
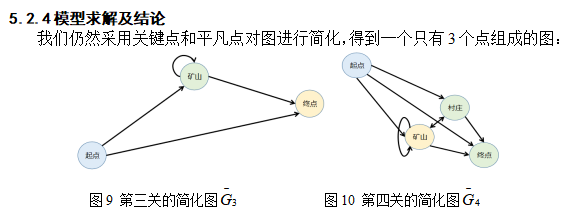
由性质3与性质4模型路线可以进一步简化，关健点之间的最短路径，可以简化为单向通道的通路。




图7：第一关简化图 图8：第二关简化图

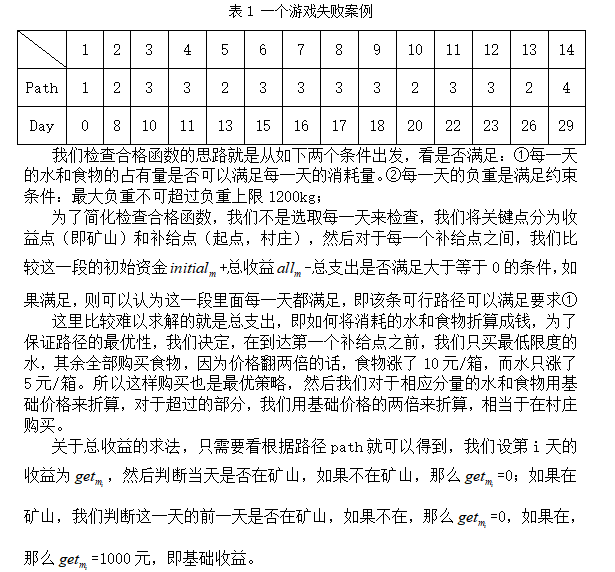
（3）检查合格函数
等到最短路径后，我们可以算出相应的收益，但是我们发现5.13(2)算出的可行路径，只满足最终可以到达终点，但是我们是不知道在其穿越沙漠的过程中，是否满足①每一天的负重是满足约束条件：最大负重不可超过负重上限1200kg；②每一天的水和食物的占有量是否可以满足每一天的消耗量，如果不满足，那么游戏失败。比如如表1所示，这条路径是满足从起点到终点的可行路径，但是我们可以通过计算发现，这条路径在挖矿挖到第18天时，会因为水不足而死亡，从而游戏失败，所以为了弥补5.1.3中寻找出来的可行路径的不足，我们决定再写一个检查合格函数，来判断可行路径中那些是可以成功完成游戏的，并且把可以成功穿越沙漠的路径保存下来，分布计算相应的收益，找出收益最大值，然后把相应的收益和路径，以及每天消耗的水和食物显示出来。





5.2.2天气的概率分布（二）
对于第四关，考虑到虽然有沙暴天气，但是沙暴天气出现次数较少，所以在5.2.1讨论的三种情况下，我们再来考虑带有沙暴的情况。同5.2.1，为了模型是实用性，我们决定通过以下几种可能情况加以讨论分析，当然不考虑极端情况，即10天的天气不可能全是晴天或者高温，因此，分如下三种情况：
①相较于高温，晴朗天气较多
由于第三幅图形状和新疆相似，并且此时，由于高温天气较多，晴朗天气较少，所以我们收集了新疆春天的天气数据，得到晴朗天气和高温天气的比例大概
（1）相较于高温，晴朗天气较多
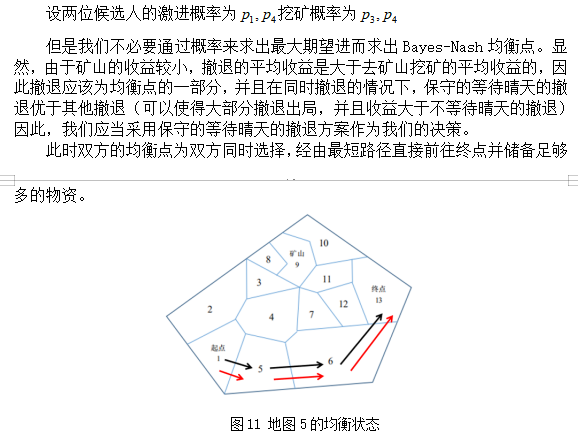
此时，由于晴朗天气较多，因此我们还是选择挖矿，因为在晴朗天气挖矿的收益较于消耗来说，是较大的，因此收益是正的，所以，我们的结论是：先从起点1 到达矿山9进行挖矿，然后从矿山9挖到留下足够到终点的粮食后，从矿山9出发，到终点13，完成比赛。

（2）相较于晴朗，高温天气较多
此时，由于高温天气较多，因此我们选择直接到达终点，因为在高温天气挖矿的收益较于消耗来说，是较小的，因此收益是负的，所以，我们的结论是：直接从起点1以着最短路径到达终点13，完成比赛。

（3）高温天气和晴朗天气相当
此时，由于高温天气和晴朗天气相当，因此实际上较难判断，因为不知道第二题的天气情况，我们无法做出决策，明天是留下来挖矿，还是去终点，所以这时的决策较为开放，可以交给玩家选择，对于较为保守型玩家，可以选择直接去终点，即：直接从起点1以着最短路径到达终点13，完成比赛。但是对于冒险性玩家，可以先去矿山挖矿，如果连续几天都是晴朗天气，那么可以等到第一次遇到高温就去终点13，让损失最小化，如果连续几天都是高温，那么由于高温天气和晴朗天气相当，所以可以继续挖矿等待晴天，等到赚回了亏本的资金，就前往终点13。
5.3问题三
5.3.1模型建立
在考虑非合作情况下，有n名玩家在相同的条件下出发。最优的决策应当是模型的Bayes-Nash均衡点，由于Bayes-Nash均衡点的最优性，当玩家选择Bayes-Nash均衡作为自己的决策时，其他玩家不论采取什么方案，不论是否相互影响，均小于等于Bayes-Nash均衡点带来的收益[1]。
在玩家互不影响的情况下Nash均衡即为我们所寻找的最优解，但是在相互影响的情形下，Nash均衡点可能会产生偏移[2]。我们建模的目标就是找到Bayes-Nash均衡点。
在地图五中，这是一个不完全信息静态博弈由于在一个有限静态Bayes博弈中（即博弈方n为有限数，并且决策集和结果集为有限集），存在Bayes-Nash均衡，并且同完全信息静态博弈相同，可能存在混合策略。
我们认为，每个博弈者可以采取以下策略去进行博弈：
（1）保守挖矿，带好需要和另一名玩家消耗的食物和水，并且去挖矿产生收益。
（2）保守撤退，带好需要和另一名玩家消耗的食物和水，并且直奔终点。
（3）激进挖矿，带好一个人使用的水和食物，并且去挖矿产生收益。
（4）激进撤退，带好一个人使用的水和食物，并且直奔终点。
我们可以使用Harsany转换，将其转化为一个完全但不完美信息动态博弈进行分析：
（1）引入一个虚拟博弈方：自然，他为每个博弈方赋予各自的类型（保守挖矿，保守撤退，激进挖矿，激进撤退）由此构建类型向量t=（a，b），其中a，b代表两位博弈者所选择的策略。
（2）自然让每一个博弈方知道自己的类型，但不让其他博弈方知道相互的类型。
（3）所有博弈方同时开始行动并且选择自己的行动方案。
（4）除了自然外，计算其余博弈方取得的收益。
在地图六中，玩家在第二天即可知道其余人的属性：激进或者保守，因为保守的人更倾向带更多的水和食物出发进行挖矿以及撤退，相当于空口声明博弈中的声明部分，但是仍然可以通过走不同的路径进行风险规避以及对其他玩家进行“威胁”（例如保守玩家靠近一个激进玩家的时候，就可以视为一种威胁），发送者的纯策略有：
（1）表明挖矿意图
（2）表明撤退意图
（3）保守玩家表明想让激进玩家出局的消耗意图
（4）激进玩家的避险意图（防止由于保守玩家的消耗而出局）
而接受者可以采取的策略为
（1）挖矿
（2）撤退
（3）绕远路回避
（4）与对方进行消耗
在这里，我们认为杂合（Hybrid）策略是不适合作为自己的策略的，由于其高概率会出局游戏或者在终点留下大量剩余水和食物。

5.3.2模型求解

地图五中，可以对各个方案进行比对：
（1）如果A玩家选择保守挖矿，B玩家选择激进挖矿；或者A玩家使用保守撤退，B玩家使用激进撤退都会使得B玩家因为水和食物缺乏而直接出局。
（2）如果A玩家选择激进挖矿，B玩家选择激进撤退，那么A玩家的得分将会低于B玩家而失败。
（3）如果A玩家使用激进挖矿，B玩家使用保守撤退，那么那么A玩家的得分将会高于B玩家而胜利。
（4）如果A玩家和B玩家同时选择激进挖矿与激进撤退，那么A玩家与B玩家都将因为食物和水不足而出局。
（5）如果A玩家选择激进撤退，B玩家选择保守挖矿，那么A玩家将会因为得分较高而胜利。
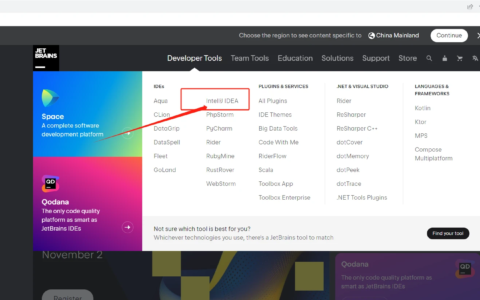
（6）如果单人模式下，最优方法为等待晴天的撤退方案。

在地图六中，注意到在村庄购买的成本大幅度上升，因此本文研究得出，如果使用保守的策略进行游戏，将会在保留威慑力的情况下节省大量金钱，相反的，如果采取激进的方式进行游戏，面对保守玩家的威胁行动时只能采取去村庄买高价的补给或者说是直接出局游戏，并且当拥有大量物资的玩家靠近只剩下少量物资的玩家时，类似于企业并购中的信号传递模型，由于不确定多物资玩家接下来的策略，少物资玩家有高概率选择撤退来使得自己不从游戏中出局，从而物资较多的玩家可以进入村庄，矿山，等关键点来获得高额收益，由于这个限制条件的存在，我们的尽可能挖矿的理论在这一处失效，因为尽可能挖矿虽然可以使得当前收益最高，但是却会降低未来挖矿收入期望。

5.3.3结论

我们对于三人的特殊情况进行局部分析：
（1）当村庄内有玩家，若该玩家的钱大于全场所有人的金钱时，其他玩家在村庄内补给的损耗将会大大上升。
（2）当村庄内有玩家，但是存在一个其他玩家金钱多于该玩家（计入物资的四倍），金钱较多的玩家可以从村庄中逼退钱较少的玩家。
（3）当其他两个玩家存在威胁关系时，村庄中停留是最好的选择。
（4）开局直接前往终点会使得其他两名玩家的钱至少一个多于你。
（5）高温天气移动将大量的减少自己的期望收入。
（6）高温与沙暴中挖矿将极大量的减少自己的期望收入。
我们可以得到改情况下的Bayes—Nash均衡，在第二问的结论之外，还要采取以下方案：
1.一开始需要购买尽可能多的资源保持自己有着足够的威慑力，并且应当在储备均匀的情况下（能够在三个人都前往村庄的情况下），尽可能多的储备质量价格比大的食物，
2.然后前往村庄（地块14）进行补给，之后补给完后前往矿山挖矿（此时的威慑力最大）到达矿山后开始挖矿，在被威慑离开后继续去村庄补给，
3.如果在村庄有人时选择在村庄外面停留，另外两人存在互相威胁关系时选择在村庄内部停留。
4.整个过程中如无出局危险，高温天气选择停留。并且在高温与沙暴天气不挖矿。

六、模型评价与推广
6.1模型优点
1.在问题1中，我们考虑了水和食物价格增长量的不同，做出了最优的初始购买方案，可以使得我们最终的收益最大化，并且该方案不影响决策，即对最优路径是没有影响的，具有独立性，因此这里的局部最优是全局最优的一部分。
2.在问题1中，为了简化图形的复杂度，我们采用平凡点和关键点对图像进行分析讨论，最终根据我们发现并且证明的最优路径的6条性质，我们可以将图只留下关键点，这样可以有效降低我们的运算复杂度。
3.在问题2中，我们采用独立同分布，这样我们可以直接采用水消耗和食物消耗的均值来分别作为每一天的水消耗和食物消耗，这样可以有效的降低计算难度和条件难度，相当于把不确定的天气因素导致的不确定的消耗量转化为确定的消耗量。
4.在问题3中，我们观察问题的对称性，并引用大量的博弈论已知结论，可以大规模的简化计算，并且我们可以较为便捷的得出答案，即本博弈问题的Bayes-Nash均衡点，从而求解问题。

6.2模型缺点
1.在地图六中使用了局部分析的技巧，虽然大规模的简化了问题，但是使得问题难于推广到其他的博弈问题中，并且难以得到定量的分析说明。

6.3模型推广
1.关于第一问的模型：这是一个类似于背包问题的优化模型，可以用来解决其他的实际问题。例如，当已知所需要的两种工业原料以及工厂的排班计划为工厂制定更高生产力的方案，其中工业原料的储存需要经费且存在损耗，工厂存在休息日以及调休情况。只需要直接使用我们第一次简化后的模型来进行求解，我们可以转化为相同的问题再用层次遍历法及条件减支的方式求解问题。
2.关于第二问的模型：引入概率变量后，我们可以建立一个高效的学习计划模型，即每天存在学习效率上的差别，并且如果有事，当天可能无法进行学习，学习知识在不复习的情况下会遗忘，并且只在当天才知道自己的学习效率以及是否有事。我们可以运用我们的随机优化方法对其进行优化，来制定高效的学习计划。以及，我们可以推广一个有预报机制的模型，预报的准确率随时间跨度的上升而下降，只需要改变我们的马尔可夫概率即可完成对该模型的求解。
3.关于第三问的模型：我们第三问使用了经典博弈论与概率论相结合的方法进行建模。广度上，我们可以将其推广到许多方面，例如，新兴产业崛起后的新领域企业竞争，短距离的小商品市场竞争。在深度上，我们可以推广到初始条件不平等的情况下，我们此时必须对于两种不同的情况进行分析，这将打破我们使用的对称性，将我们转移到重新使用概率进行繁琐的判断的情况，并对概率函数进行拉格朗日乘因子法进行求解的做法，以及含有预报机制的情况，我们需要更多的结合所知的天气以及第二问的马尔可夫性对其进行建模。
七、参考文献
[1]博弈论及其应用 科学出版社
[2]蒲勇健的博弈论与经济模型，中国人民大学出版社
[3]Shin Harase. A table of short-period Tausworthe generators for Markov chain quasi-Monte Carlo. 2021, 384
[4]Yuyao Wang, Zhan Bu, Huan Yang, et al. An effective and scalable overlapping community detection approach: Integrating social identity model and game theory. 2021, 390
[5]Valentino Tascione, Raffaele Mosca, Andrea Raggi. A proposal of an economic optimization model for sustainable waste management. 2021, 279
[6]韩霖.迷宫问题中最短路径问题的探究[J].电脑知识与技术,2018,14(33):55-57.
[7]宋佳佳. 部分观测马尔科夫决策过程中基于记忆的强化学习问题研究[D].天津工业大学,2017.