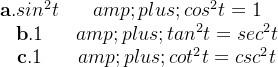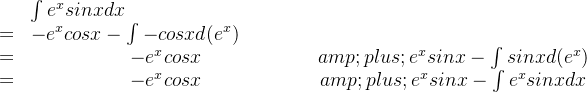目录
原函数的概念
不定积分
定义
不定积分的基本积分公式
不定积分的运算法则
求原函数的两种常用方法
第一换法(凑微分法)
第二换法
分部积分法
有理函数原函数求法
典型三角函数原函数求法
原函数的概念
设
在区间
上有定义,若存在函数
,对任意
,都有
或
.
则称
为
在区间
上的一个原函数。
例:由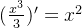
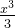
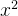

由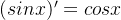
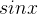
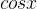

因为:
所以:原函数可以表达为
不定积分
定义
函数
的全体函数
称为
的不定积分,记作
,即
其中,“
”表示积分号,
为被积函数,
为被积表达式,
为积分变量,
为积分常数。
不定积分的基本积分公式
不定积分的运算法则
(1)被积函数中不为0的常数因子可以提出来:
(2)两个函数代数和的不定积分等于这两个函数不定积分的代数和
求原函数的两种常用方法
第一换法(凑微分法)
例:
一、找到复合函数
二、由
三、换,令u=sinx
四、求出来后回代
要熟练应用第一换法,需要有效地凑出:
第二换法
例:
令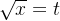

第二换法积分公式:
第二换法的三角换法
当被积函数中含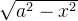
当被积函数中含
当被积函数中含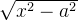
分部积分法

于是,得到分部积分公式:
例:
特殊题型
移到等式左边
需要对左式再进行分部积分。
有理函数原函数求法
典型三角函数原函数求法
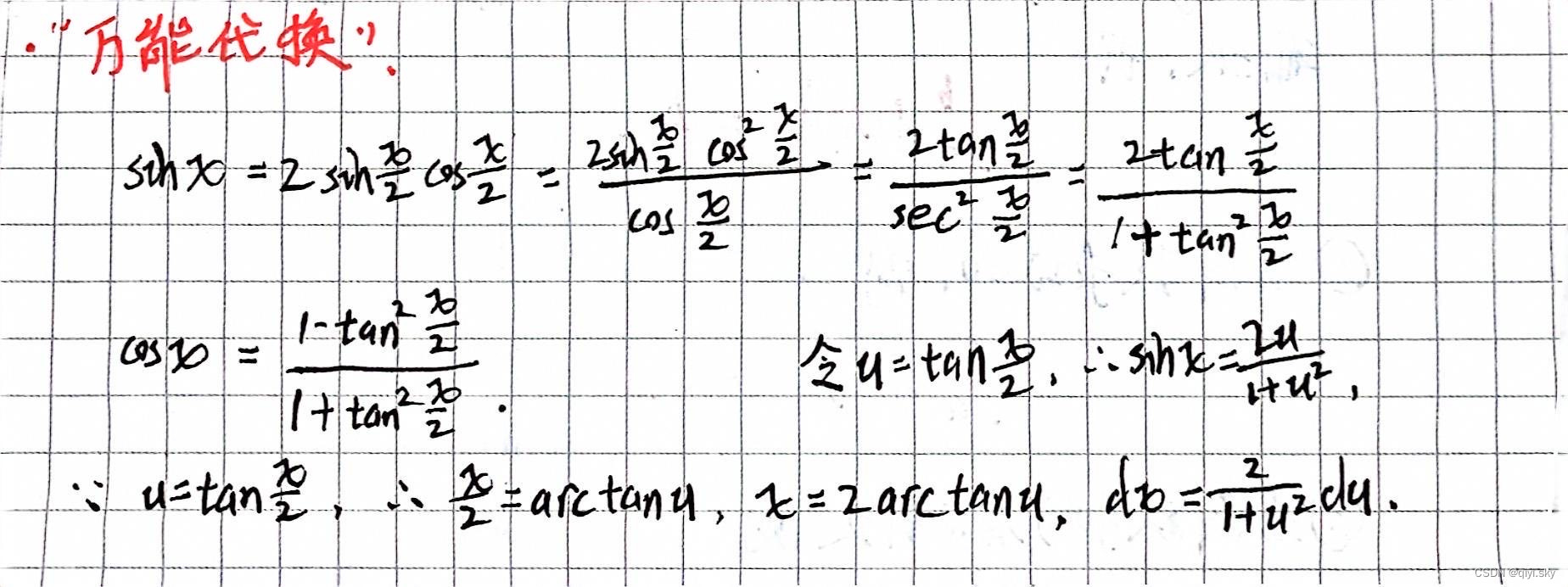
end
2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/164134.html

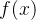 在区间
在区间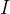 上有定义,若存在函数
上有定义,若存在函数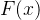 ,对任意
,对任意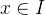 ,都有
,都有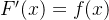 或
或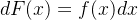 .
.
 称为
称为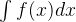 ,即
,即
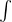 ”表示积分号,
”表示积分号,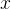 为积分变量,
为积分变量,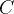 为积分常数。
为积分常数。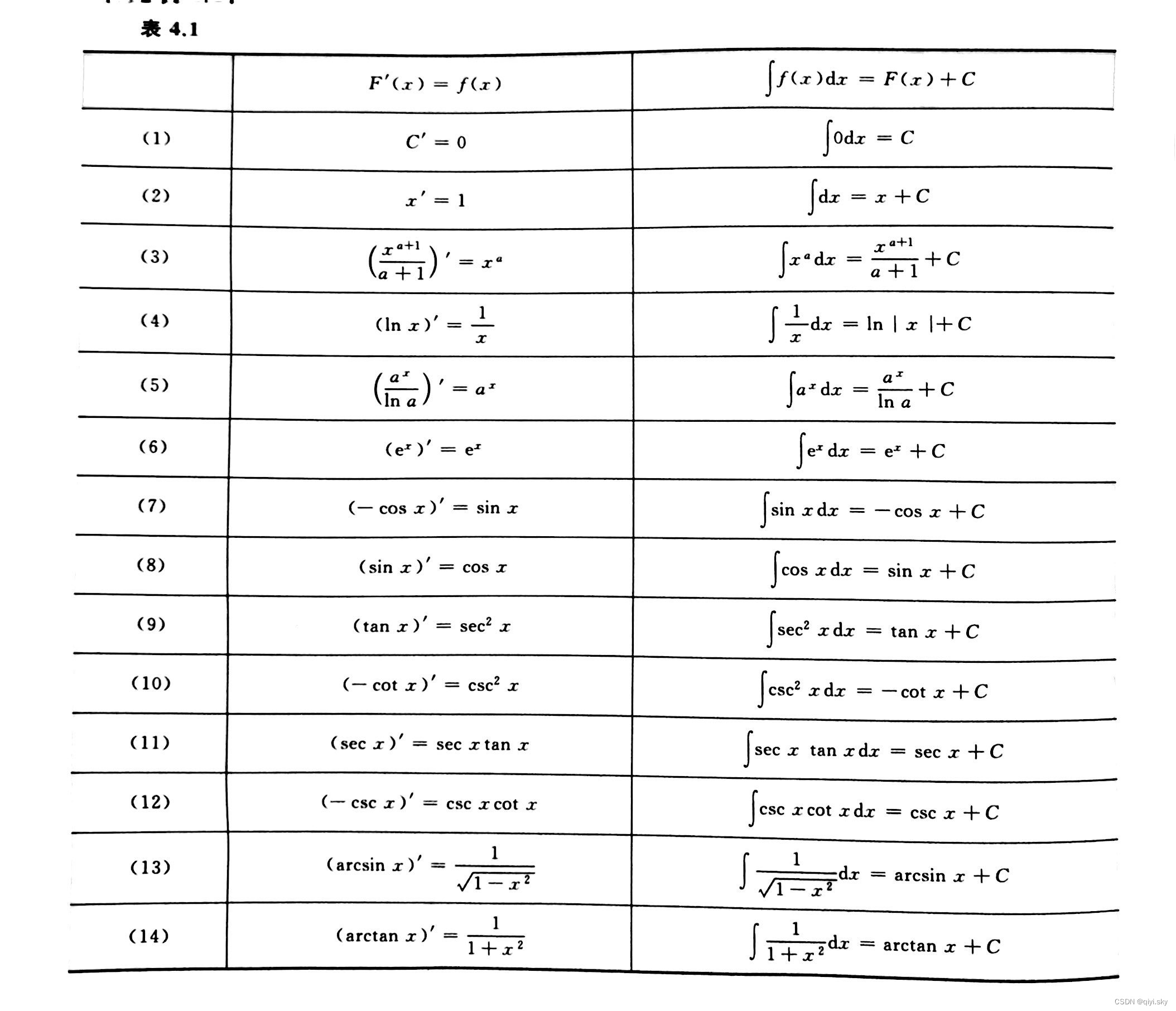

![求原函数方法_求原函数方法插图49 \int [f_1(x)\pm f_2(x)]dx=\int f_1(x)dx\pm \int f_2(x)dx](https://sigusoft.com/wp-content/uploads/2024/07/4GQH1mA3be.png%20%5Bf_1%28x%29%5Cpm%20f_2%28x%29%5Ddx%3D%5Cint%20f_1%28x%29dx%5Cpm%20%5Cint%20f_2%28x%29dx)

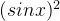
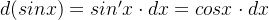



![求原函数方法_求原函数方法插图63 f[\varphi (x)]\varphi '(x)dx=f(u)du](https://sigusoft.com/wp-content/uploads/2024/07/0494vI6A2.png)

![求原函数方法_求原函数方法插图73 \int f(x)dx=G[\varphi^{-1}(x) ]+C](https://sigusoft.com/wp-content/uploads/2024/07/4qMer.png%3DG%5B%5Cvarphi%5E%7B-1%7D%28x%29%20%5D+C)