金融学习之十六——资本市场线

2024年 7月 4日下午10:47 • 激活谷笔记

前面两讲在进行投资组合配置时均只考虑到了有风险的资产，而实际在进行投资时，也有可能包含无风险资产（如国债），在这种状况下进行投资，又会出现什么特点呢？这就要引出另一个概念——资本市场线。
资本市场线（CML）是一条从无风险收益率引出的与有效前沿相切的一条直线，该直线的斜率仅与无风险收益率相关，因此当无风险收益率确定时，该直线也就确定下来了。
在知乎上看到两张图片，对这个资本市场线的解释非常详细，于是我就借用过来，大致说说吧。文章地址为：

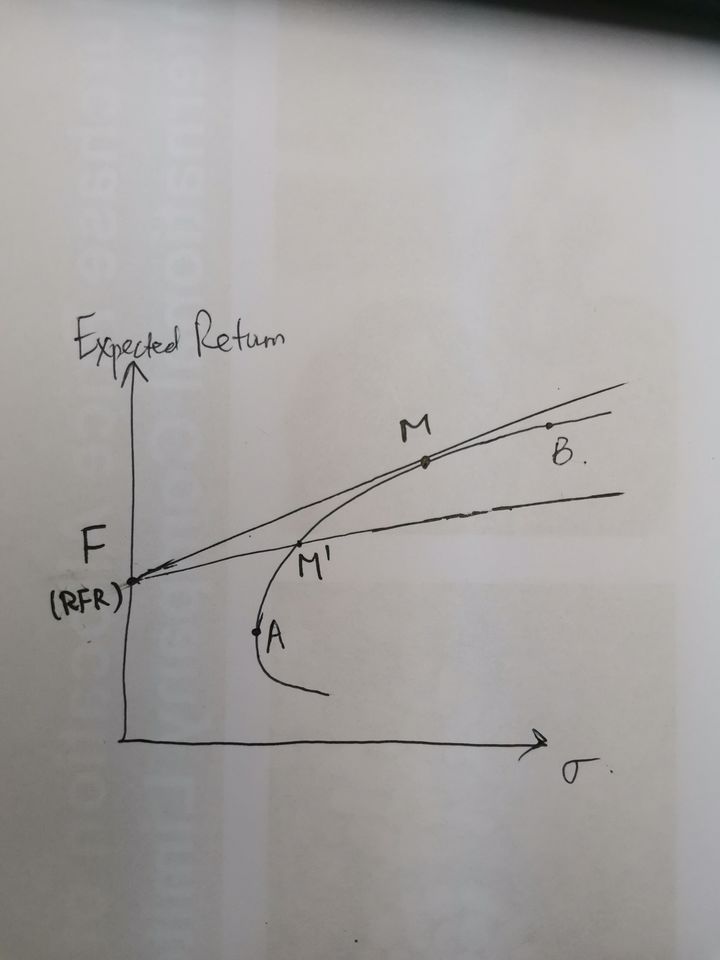
从这张图中可以看出，资本配置线是当引入无风险资产后，从无风险收益率引出的一条射线，其斜率为 $(E(R)-Rf)/\sigma_p$ ，即期望收益与无风险收益之差与收益率波动率的比值，这个比值也称为夏普比率。

从这张图上又可以看出，当无风险收益率确定时，资本配置线是可以有很多条的，但仅有一条能与有效前沿相切，那么这条线就是资本市场线，切点所对应的投资组合称为市场组合。而且，从这些线也可以发现，对于可行集来说，在风险（x）相同时，资本市场线可以达到最大的收益率（y）；在收益相同时（y），资本市场线可以取得最小的风险（x）。
因此，资本市场线的斜率实际上可以转化为带有约束的方程求最优解：
约束条件为 $\displaystyle \sum_{k=1}^n w_i =1$ ， $w_i$ >0,方程为
$max\ (E(R_p)-R_f )/ \sigma_p$
下面，我们假设无风险利率为3%/年，依然利用前面的数据，来绘制资本市场线。整个过程我们再重新做一遍：

#获取股票基本信息表，目的是为了拿到前几个股票的代码 import tushare as ts pro=ts.pro_api('ba3ddd7dde8ebe28bb2f8356c918ad80dae01605b') df=pro.stock_basic(exchange='', list_status='L', fields='ts_code,symbol,name,area,industry,list_date') df.head()

接着获取数据，并进行处理后，计算收益率：

import pandas as pd dt=pd.DataFrame() for i in df.loc[:5][['ts_code','name']].values: dt[i[1]]=pro.daily(ts_code=i[0], start_date='', end_date='')['close'] dt.drop('国华网安',axis=1,inplace=True) import numpy as np r=np.log(dt/dt.shift(1)) r=r.dropna() r

再计算出相关的年化收益率、协方差系数、相关系数和波动率

r_mean=r.mean()*252 r_cov=r.cov()*252 r_corr=r.corr() r_vol=r.std()*np.sqrt(252) r_mean,r_cov,r_corr,r_vol

绘制出投资组合的可行集：

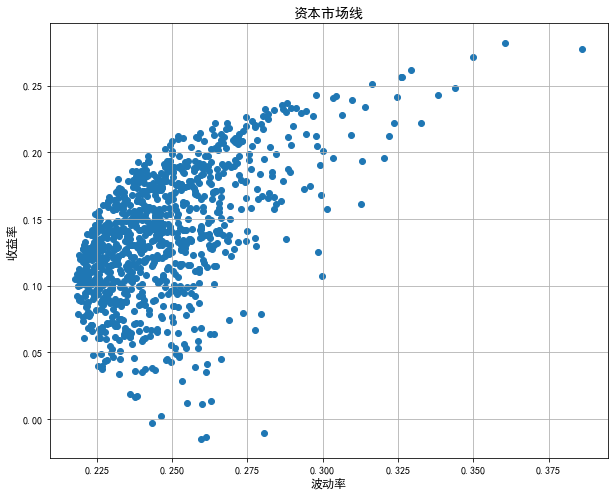
from pylab import mpl mpl.rcParams['font.sans-serif']=['SimHei'] mpl.rcParams['axes.unicode_minus']=False rp=[] vp=[] for i in np.arange(1000): x=np.random.random(5) weights=x/sum(x) rp.append(np.sum(weights*r_mean)) vp.append(np.sqrt(np.dot(weights,np.dot(r_cov,weights.T)))) plt.figure(figsize=(10,8)) plt.scatter(vp,rp) plt.xlabel(u'波动率',fontsize=12) plt.ylabel(u'收益率',fontsize=12,rotation=90) plt.title(u'资本市场线',fontsize=14) plt.grid('True') plt.show()

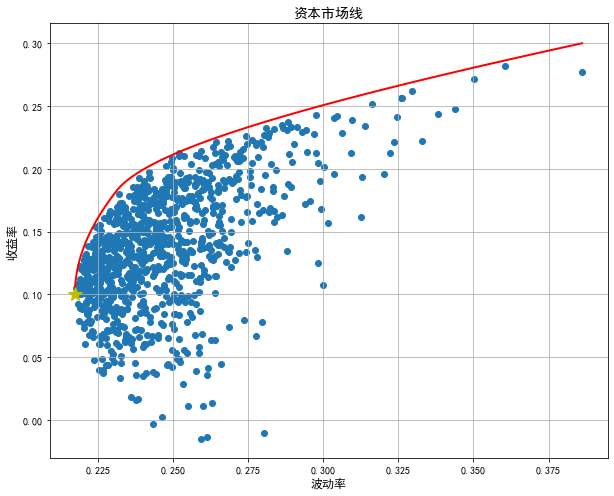
再计算并绘制出有效前沿：

import scipy.optimize as sco def f(w): w=np.array(w) rp=np.sum(w*r_mean) vp=np.sqrt(np.dot(w,np.dot(r_cov,w.T))) return np.array([rp,vp]) def vmin(w): return f(w)[1] cons=({ 
   'type':'eq','fun':lambda x:np.sum(x)-1}) bnds=tuple((0,1) for x in range(len(r_mean))) result_min=sco.minimize(vmin,len(r_mean)*[1.0/len(r_mean),],method='SLSQP',bounds=bnds,constraints=cons) rp_min=np.sum(r_mean*result_min['x']) vp_min=result_min['fun'] rpt=np.linspace(rp_min,0.3,100) vpt=[] for i in rpt: cons=({ 
   'type':'eq','fun':lambda x:np.sum(x)-1},{ 
   'type':'eq','fun':lambda x:f(x)[0]-i}) result=sco.minimize(vmin,len(r_mean)*[1.0/len(r_mean),],method='SLSQP',bounds=bnds,constraints=cons) vpt.append(result['fun']) plt.figure(figsize=(10,8)) plt.scatter(vp,rp) plt.plot(vpt,rpt,'r-',label=u'有效前沿',lw=2) plt.plot(vp_min,rp_min,'y*',label=u'全局最小波动率',markersize=14) plt.xlabel(u'波动率',fontsize=12) plt.ylabel(u'收益率',fontsize=12,rotation=90) plt.title(u'资本市场线',fontsize=14) plt.grid('True') plt.show()

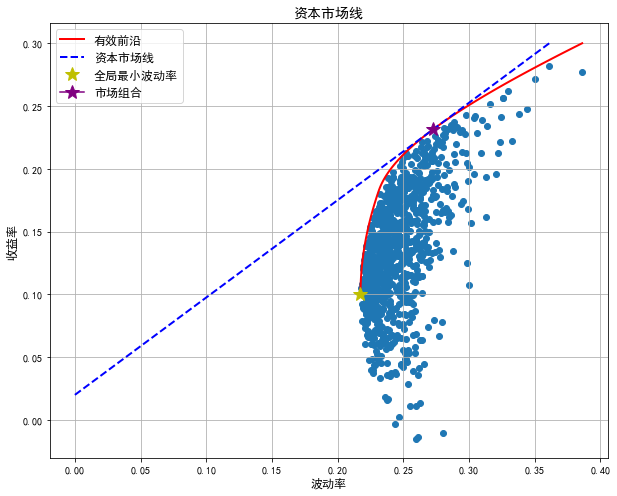
接着假定无风险收益率为2%，计算出资本市场线斜率和市场组合，并进行绘制：

#定义相关函数 def ff(w): rf=0.02 w=np.array(w) rp=np.sum(w*r_mean) vp=np.sqrt(np.dot(w,np.dot(r_cov,w.T))) sharp=(rp-rf)/vp return np.array([rp,vp,sharp]) def spmin(w): return -ff(w)[2]

#计算市场组合 cons1=({ 
   'type':'eq','fun':lambda x:np.sum(x)-1}) result_s=sco.minimize(spmin,len(r_mean)*[1.0/len(r_mean),],method='SLSQP',bounds=bnds,constraints=cons1) rf=0.02 slope=-result_s['fun'] rm=np.sum(r_mean*result_s['x']) vm=(rm-rf)/slope print(slope,rm,vm)

#绘制整个图形 rp_cml=np.linspace(0.02,0.3) vp_cml=(rp_cml-rf)/slope plt.figure(figsize=(10,8)) plt.scatter(vp,rp) plt.plot(vpt,rpt,'r-',label=u'有效前沿',lw=2) plt.plot(vp_cml,rp_cml,'b--',label=u'资本市场线',lw=2) plt.plot(vp_min,rp_min,'y*',label=u'全局最小波动率',markersize=14) plt.xlabel(u'波动率',fontsize=12) plt.ylabel(u'收益率',fontsize=12,rotation=90) plt.title(u'资本市场线',fontsize=14) plt.legend(fontsize=12) plt.grid('True') plt.show()

最后得到资本市场线的图形：

金融学习之十六——资本市场线

相关推荐