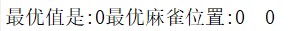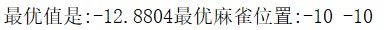麻雀搜索算法流程图_matlab预测模型

2024年 6月 30日 10:16 • 激活谷笔记

麻雀搜索算法是2020年提出的启发式算法，算法的具体过程见下面链接

https://blog.csdn.net/weixin_/article/details/

https://blog.csdn.net/u0/article/details/

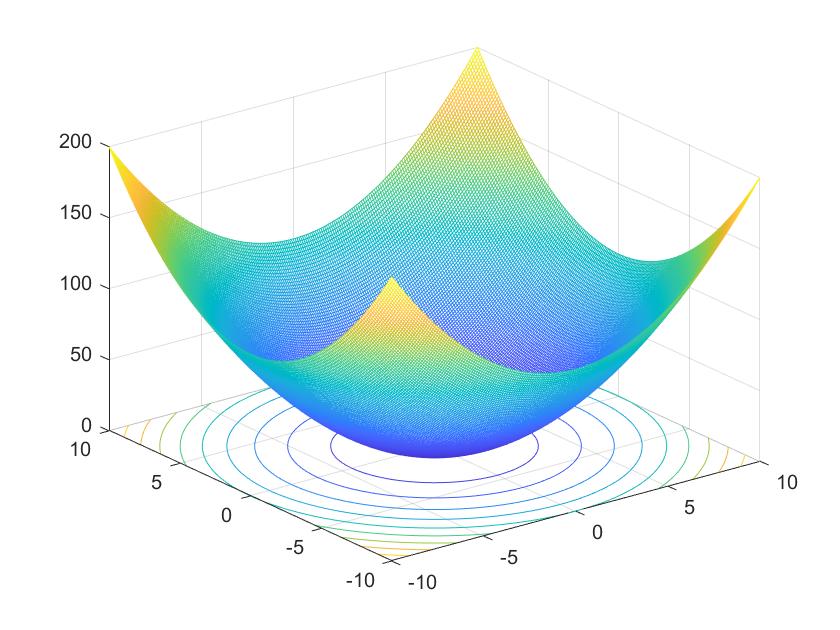
个人写的麻雀搜索算法的Matlab代码，仅供参考，由于算法的一些变量介绍的并不是很清楚，所以就自己凭感觉写的。算法的测试函数如下：

$y=\sum _{i=1}^{n}x_i^2$

三维的matlab图像如下：

在自变量上下限为10，-10，有一个全局最优解 ${x}_{1}={x}_{2}=0$ ， y=0

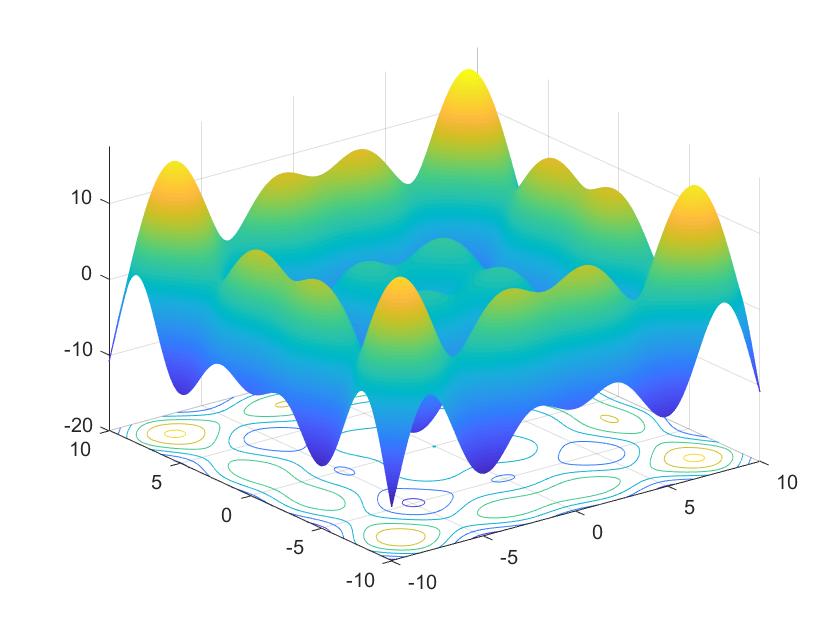
第二个测试用例如下：

$y=\sum _{i=1}^{n}{x}_{i}*sin({x}_{i})+0.1*{x}_{i}$

它三维的matlab图像如下：

在自变量上下限为10，-10时，这个函数在四个边界点(10,10) (-10,-10) (-10,10) (10,-10)有最小值。

Matlab代码如下：

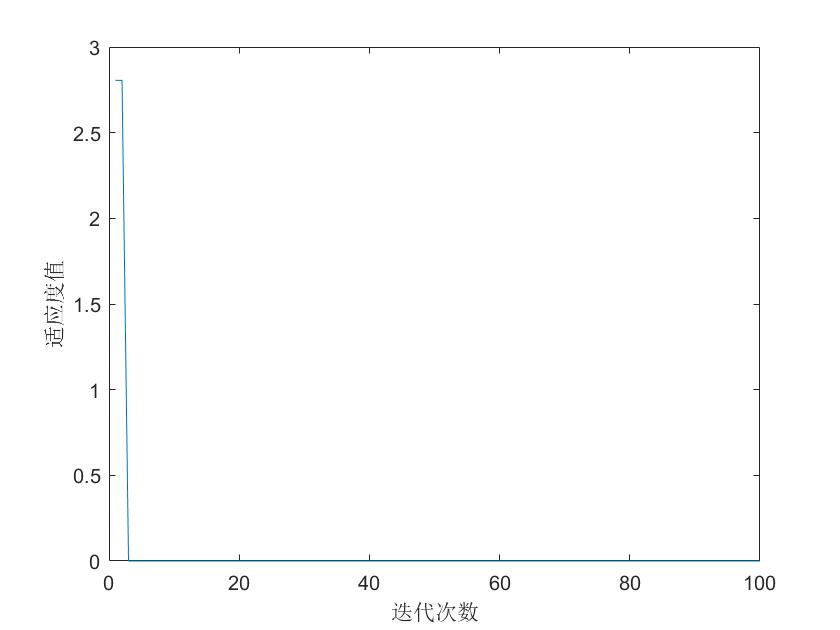
clear all; close all; clc; %% 参数设置 N=30; %麻雀个数 dim=2; %评估函数维度 N_discoverer=0.7*N; %发现者个数 N_Followers=0.1*N; %追随者个数 N_Vigilant=0.2*N; %警戒者个数 Max_iter=100; %最大迭代次数 ST=0.6; %安全阈值 %% 测试函数 f=@(x) sum(x.^2); ub=10;%边界上限 lb=-10;%边界下限 %% 初始化 x=lb+rand(N,dim).*(ub-lb); %初始化麻雀种群 for i=1:N fitness(i)=f(x(i,:)); %计算麻雀种群的适应度值 end [A,index]=sort(fitness); x_best=x(index(1),:); %记录所有麻雀走过的位置的最优位置 x_worst=x(index(end),:); %记录所有麻雀走过的位置的最差位置 best_fitness=A(1); %记录所有麻雀走过的位置的最优值 worst_fitness=A(end); %记录所有麻雀走过的位置的最差值 x_best_currently=x(index(1),:); %记录当前麻雀种群最优位置 x_worst_currently=x(index(end),:); %记录当前麻雀种群最差位置 best_fitness_currently=A(1); %记录当前麻雀种群最优值 worst_fitness_currently=A(end); %记录当前麻雀种群最差值 x_discoverer=x(index(1:N_discoverer),:); %发现者位置 x_Followers=x(index(N_discoverer+1:N_discoverer+N_Followers),:); %追随者位置 x_Vigilant=x(index(N_discoverer+N_Followers+1:N),:); %警戒者位置 B=[-1,1]; F=best_fitness; %记录每次迭代的麻雀走过的位置的最优值 iter=1; %初始化迭代次数 %% 开始迭代更新 while iter<Max_iter for i=1:dim C(i)=B(round(rand)+1); end A=C'*inv((C*C')); R2=rand; %更新发现者位置 for i=1:N_discoverer for j=1:dim if R2<ST x_discoverer(i,j)=x_discoverer(i,j)*exp(-i/rand*Max_iter); else x_discoverer(i,j)=x_discoverer(i,j)+randn; end end %边界判断 ub_flag=x_discoverer(i,:)>ub; lb_flag=x_discoverer(i,:)<lb; x_discoverer(i,:)=(x_discoverer(i,:).*(~(ub_flag+lb_flag)))+ub.*ub_flag+lb.*lb_flag; end %更新追随者位置 for i=1:N_Followers for j=1:dim if i>N/2 x_Followers(i,j)=rand*exp((x_worst_currently(j)-x_Followers(i,j))/i^2); else x_Followers(i,j)=x_discoverer(1,j)+abs(x_Followers(i,j)-x_discoverer(1,j))*A(j); end end %边界判断 ub_flag=x_Followers(i,:)>ub; lb_flag=x_Followers(i,:)<lb; x_Followers(i,:)=(x_Followers(i,:).*(~(ub_flag+lb_flag)))+ub.*ub_flag+lb.*lb_flag; end %更新警戒者位置 for i=1:N_Vigilant for j=1:dim if f(x_Vigilant(i,:))~=best_fitness_currently x_Vigilant(i,j)=x_best_currently(j)+randn*abs(x_Vigilant(i,j)-x_best_currently(j)); else x_Vigilant(i,j)=x_Vigilant(i,j)+B(round(rand)+1)*(abs(x_Vigilant(i,j)-x_worst_currently(j)))/abs(f(x_Vigilant(i,:))-worst_fitness_currently)+1; end end %边界判断 ub_flag=x_Vigilant(i,:)>ub; lb_flag=x_Vigilant(i,:)<lb; x_Vigilant(i,:)=(x_Vigilant(i,:).*(~(ub_flag+lb_flag)))+ub.*ub_flag+lb.*lb_flag; end x=[x_discoverer;x_Followers;x_Vigilant]; %得到该次迭代下的所有麻雀的新位置 for i=1:N fitness(i)=f(x(i,:)); %计算适应度 end [E,index]=sort(fitness); if f(x(index(1),:))<best_fitness %更新所有麻雀走过的位置的最优位置和最优值 best_fitness=f(x(index(1),:)); x_best=x(index(1),:); end if f(x(index(end),:))>worst_fitness %更新所有麻雀走过的位置的最差位置和最差值 worst_fitness= f(x(index(end),:)); x_worst=x(index(end),:); end x_best_currently=x(index(1),:); %更新当前麻雀种群的最优位置 x_worst_currently=x(index(end),:); %更新当前麻雀种群的最差位置 best_fitness_currently=E(1); %更新当前麻雀的种群的最优值 worst_fitness_currently=E(end); %更新当前麻雀的种群的最差值 x_discoverer=x(index(1:N_discoverer),:); %重新选择种群中的发现者 x_Followers=x(index(N_discoverer+1:N_discoverer+N_Followers),:); %重新选择种群中的追随者 x_Vigilant=x(index(N_discoverer+N_Followers+1:N),:); %重新选择种群中的警戒者 F=[F,best_fitness]; iter=iter+1; %迭代次数加一 end %% 结果 作图 display(['最优值是:',num2str(F(end)),'最优麻雀位置:',num2str(x_best)]); figure(1); plot(F); xlabel('迭代次数'),ylabel('适应度值');

第一个测试函数结果：

第二个测试函数结果：

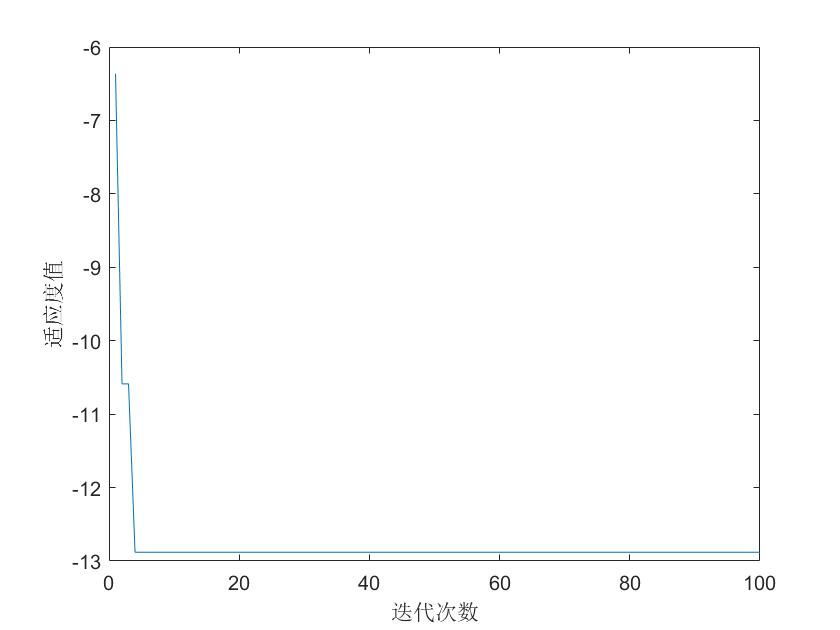
由于该算法只能找到一个最值，故只找到一个最优麻雀位置，可以看到即使在有许多极小值的测试函数中麻雀搜索算法都能够有效的找到最优值而不会陷入局部最优。

麻雀搜索算法流程图_matlab预测模型

相关推荐