题目
平面上有两个矩形,它们的边平行于直角坐标系的X轴或Y轴。对于每个矩形,我们给出它的一对相对顶点的坐标,请你编程算出两个矩形的交的面积。
输入
输入仅包含两行,每行描述一个矩形。
在每行中,给出矩形的一对相对顶点的坐标,每个点的坐标都用两个绝对值不超过10^7的实数表示。
输出
输出仅包含一个实数,为交的面积,保留到小数后两位。
样例输入
1 1 3 3 2 2 4 4 样例输出
1.00 解题思路
先判断两个矩形是否存在交集:令两个矩形的x方向上边长之和的1/2为r,y方向上的边长之和的1/2为c,若两个矩形中心点的横坐标之差、纵坐标之差(取>=0的值,大减小)分别小于r和c,则有交集;若不满足,则无交集。
若无交集,输出0.00;若有交集,再对已知四个点的x和y坐标分别进行排序,得到x1–x4,y1–y4(从小到大顺序),矩形面积即为(x3-x2)*(y3-y2)。
难点
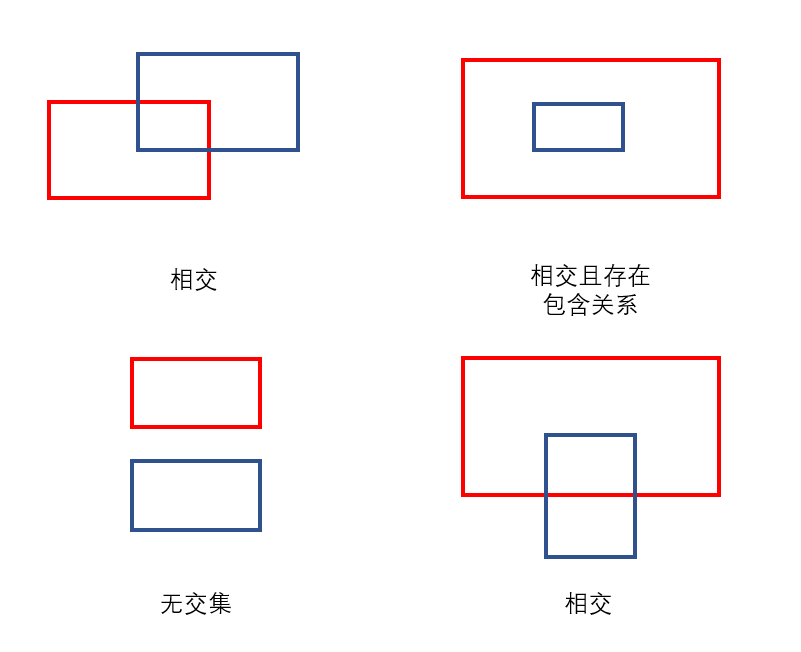
需要考虑多种情况:
- 两个矩形相交但无从属关系(即矩形A、B互不包含);
- 两个矩形中,一个为另一个子集;
- 无交集。
(首次练习时我遗漏了存在包含关系的相交情况,在解题思路上存在bug)
代码
#include<stdio.h> #include<stdlib.h> double abs_d(double a){
if (a<0) return -a; else return a; } int cmp(const void *a, const void *b){
//从小到大排序 double c = *(double *)a; double d = *(double *)b; if (c>d) return 1; else return -1; } int intersection(double x[4],double y[4]) {
double mpA[2],mpB[2];//存放中心点的坐标 double d1,d2,c[2],k[2]; c[0] = abs_d(x[0]-x[1]);//x方向矩形A的长度 c[1] = abs_d(x[2]-x[3]);//x方向矩形B的长度 k[0] = abs_d(y[0]-y[1]);//y方向矩形A的长度 k[1] = abs_d(y[2]-y[3]);//y方向矩形A的长度 mpA[0] = (x[0]+x[1])/2; mpA[1] = (y[0]+y[1])/2; mpB[0] = (x[2]+x[3])/2; mpB[1] = (y[2]+y[3])/2; d1 = abs_d(mpA[0]-mpB[0]); d2 = abs_d(mpA[1]-mpB[1]); if ((d1>(c[0]+c[1])/2) || (d2>(k[0]+k[1])/2))//无交集 return 0; else return 1; } int main(){
int i; double x[4],y[4]; for (i=0;i<4;i++) {
scanf("%lf",&x[i]); scanf("%lf",&y[i]); } int judge = intersection(x,y); if (judge==0) printf("0.00"); else {
qsort(x,4,sizeof(double),cmp); qsort(y,4,sizeof(double),cmp); printf("%0.2lf",abs_d((x[1]-x[2])*(y[1]-y[2]))); } return 0; } 注:解题思路有参考C语言网CodeRookie的解答,感谢作者分享思路!(网址:https://blog.dotcpp.com/a/77089)
2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/117167.html