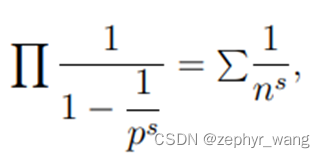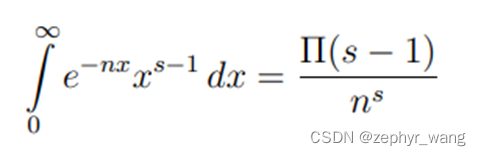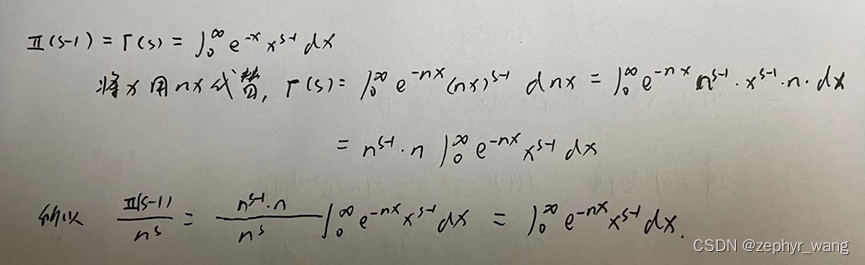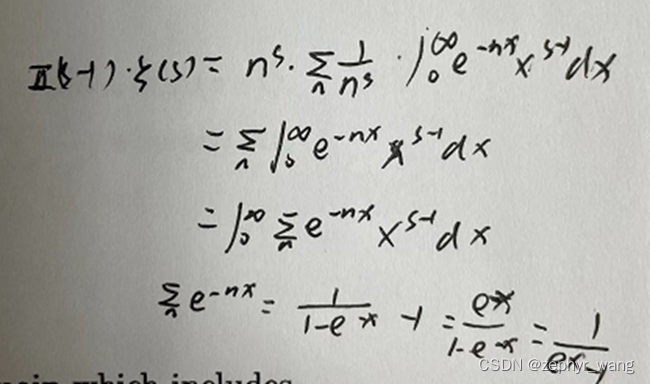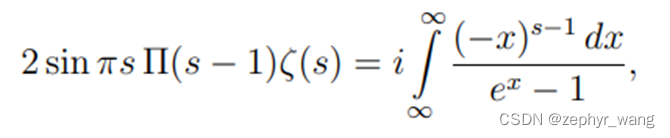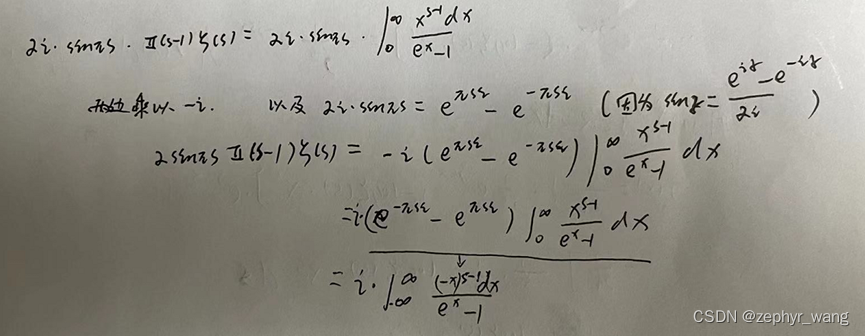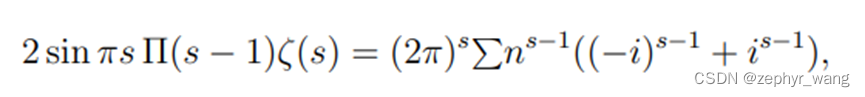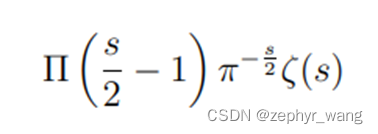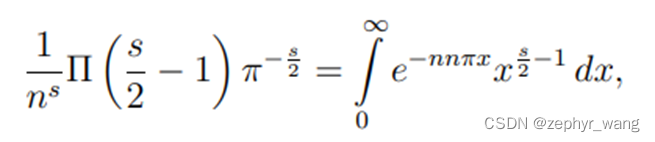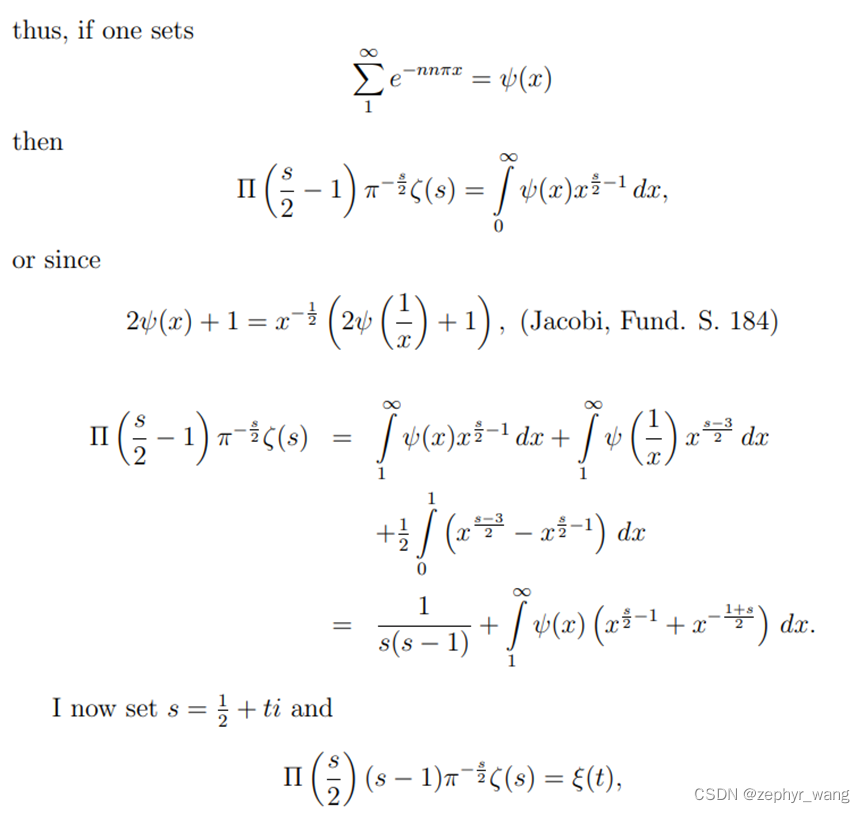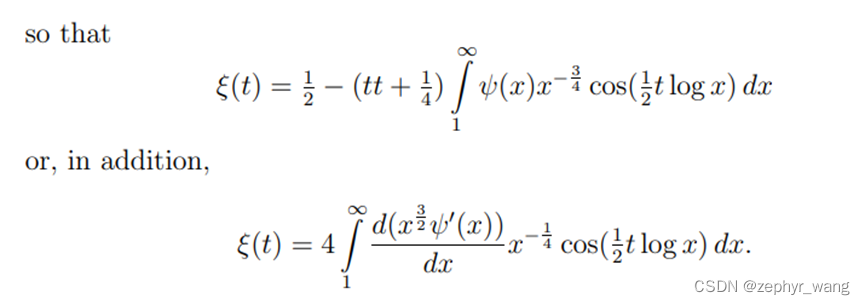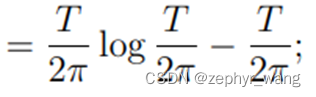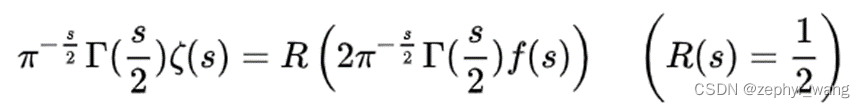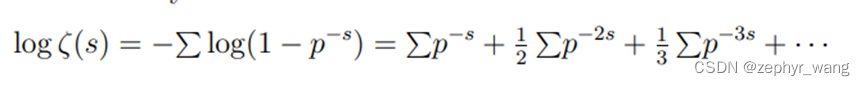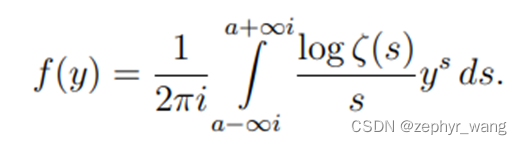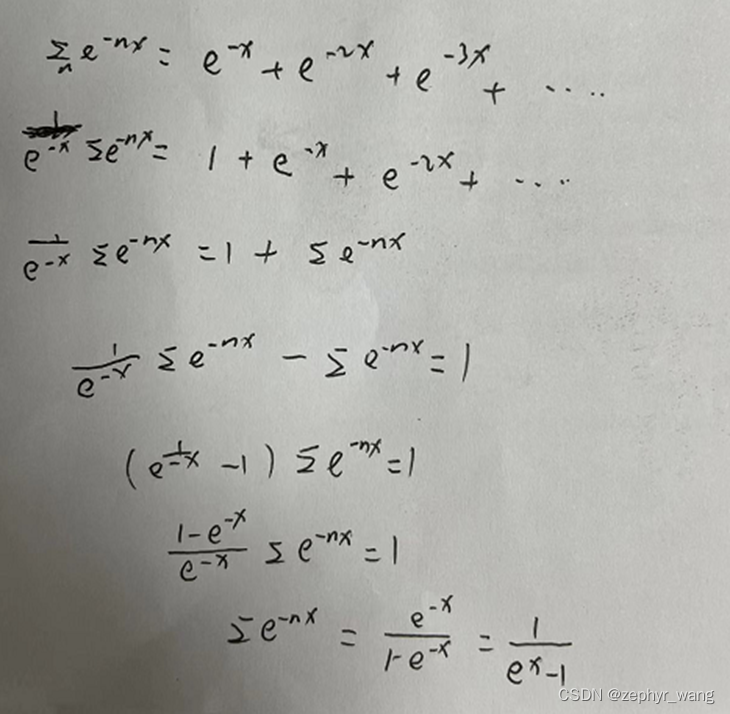黎曼猜想-黎曼1859年《论小于某给定值的素数的个数》

黎曼猜想–黎曼1859年《论小于某给定值的素数的个数》

2024年 6月 20日下午10:53 • 激活谷笔记

黎曼1859年《论小于某给定值的素数的个数》原文是德文。本文是根据1998年David R. Wilkins翻译的英文总结写的。在该文中黎曼引出了黎曼函数、黎曼猜想，并且给出了小于或等于x的素数个数π（x）的公式。

黎曼从欧拉乘积公式开始：

其中p是所有素数，n是所有数字。

将s用复数表示, 当上面两个式子收敛时，我们称为黎曼函数ζ（s）.

首先利用如下等式：

Π（s-1）是高斯引入的伽马函数符号，现在一般写作Γ(s), 即Γ(s)= Π（s-1）。证明如下：

接着可以得到

证明如下（同时见附录1）：

进而可以得到：

证明如下：

上式就给出了对所有复数s的黎曼函数ζ（s）的函数值。除了s=1，对于所有有限的s，函数值是一一对应的。当s为负的偶数时，函数值等于0.

利用留数定理，得

进而看到ζ（s）和ζ（s-1）的关系，

上式利用伽马函数特点，如果s变成1-s，上式不变。

所以，我们考虑下s/2的情况

上面用到了雅可比椭圆函数。

上面辅助函数ξ对所有有限的t是有限的，同时容许自己以t的平方的速度快速发展为一个收敛级数。对于s的实部大于1时，logζ（s）是有限的，同时辅助函数ξ（t）在t的虚部是1/2i与-1/2i之间时，等于0。ξ（t）=0的根的数量，其实部在0与T直接的数量约等于如下：

上式一直到1895年由mangoldt严格证明。

这是因为沿包含所有虚部位于1/2 i和-1/2 i、实部位于0至T之间的t值的正向回路积分∫d logξ(t)等于（T logT/2π-T）i。而该积分的值又等于ξ(t)=0的根的数量乘以2πi.

发现在该限制下实际根的数量近似该数量，而且很可能所有的根就真的是这些。可能这里需要一个严格的证明，但我进行了一些短暂的徒劳的尝试后，将其放到了一边，因其对于下面的研究其不是必须的。这就是黎曼猜想原稿。

1932年C.L.Siegel发表的文章中 [9] ，有下面这样一个公式：

文章的作者根据这个公式的几何意义以及cos函数的零点性质，直接推导出来No（T）=N（T），即证明了区域内的零点全部落在临界线上。

由黎曼函数定义知：

可以看到上式f(x)同https://blog.csdn.net/zephyr_wang/article/details/ 中的J（x）。F（x）是π（x）, 即小于或等于x的素数的个数。

上式对于s=a+bi, a>1时有效。

采用傅里叶变换，得到

可以看到上式f(x)、f(y)同https://blog.csdn.net/zephyr_wang/article/details/ 中的J（x）.

剩下的内容就类似https://blog.csdn.net/zephyr_wang/article/details/ 的第9章节。

黎曼猜想–黎曼1859年《论小于某给定值的素数的个数》